基于模糊逻辑的MEMS陀螺零漂温度补偿技术*
2011-12-10苑伟政常洪龙
秦 伟,苑伟政,常洪龙,薛 亮
(西北工业大学微/纳米系统实验室,西安710072)
0 引言
MEMS技术在惯性领域已得到广泛应用,如微机械陀螺和加速度计由于其加工材料、工艺水平等的特殊性和局限性,小型化尺寸和构造使其对周围环境的变化很灵敏。随着外界温度的变化,MEMS陀螺的各项指标,如零漂、刻度因子、灵敏度等都会发生相应改变,有些变化比较显著。并且MEMS陀螺长时间工作自身发热,同样影响其精度。以上因素会致使由其所构造的微型姿态测量的精度变差。由此需要对MEMS陀螺进行温度测试,建立可靠的温度补偿模型和补偿算法改善温度的影响。
对MEMS陀螺温度建模及补偿的相关研究,如文献[1]通过对MEMS陀螺的机理分析,提出一种无温度传感器的全温补偿型陀螺,是从器件角度进行补偿;文献[2]采用多项式分段拟合方法,对 MEMS陀螺在全温工作段(-40℃~80℃)进行分段拟合,达到温度补偿的效果;文献[3]用小波变换方法对MEMS陀螺数据进行尺度分解后,建立了温度的6阶多项式拟合模型。后两种方法虽然达到了温度补偿的效果,但均未考虑实时性问题,因为多项式拟合的次数越高,其补偿精度越高,同时计算量也就越大。在实际应用中,如微型无人机姿态控制等方面,应该使MEMS陀螺受温度的影响减至最低,并且不应占用较多的CPU资源,不应有很大的计算量。
MEMS陀螺的角速率输出跟温度之间是复杂的非线性关系,难以通过二阶或更高阶的拟合曲线来反映。模糊逻辑方法可为所有非线性问题建模提供理论依据,并且不需要建立精确数学模型。文中即从补偿精度及计算量两方面考虑,采用简化的一元Takagi-Sugeno(T-S)模糊逻辑方法对 MEMS陀螺零漂进行温度建模与补偿。
1 陀螺零偏受温度影响机理分析
MEMS陀螺的加工通常采用热敏材料的薄硅片,其物理特性受温度影响较大,由MEMS陀螺的原理可知,陀螺谐振频率与温度的关系可表示为[2]:

式中:ω(T)为温度为T时陀螺的谐振频率;T0为参考室温;kET为硅材料弹性模量随温度的变化系数,通常取10-6数量级;ΔT为相对室温的温度变化量。
因为陀螺谐振频率的漂移,对陀螺驱动模态和检测模态都有较大影响,从而引起陀螺输出的零偏稳定性和刻度因子的漂移,从陀螺结构上看,要减小温度变化对谐振频率的影响,需要采用性能更好的材料,然而实际中这将较大的增加成本[1,6]。并且即使环境温度不发生大的改变,陀螺自身工作较长时间,其内部温度也会发生改变。
在诸多指标中,陀螺零漂受温度的影响最大,而刻度因子相对来说所受影响较小[2],因此文中对MEMS陀螺零漂的温度补偿情况进行研究。图1为几个典型温度点的某型MEMS陀螺数据零漂值。

图1 陀螺零漂与温度关系曲线
由图1可知,零偏与温度值为非线性关系。要实现对MEMS陀螺的温度补偿,需在全温范围内建立准确的温度误差模型。
2 T-S模糊逻辑零漂温度补偿模型
模糊逻辑方法是通过把经验和实验结果总结成若干规则,根据规则推理,并快速完成运算。并且选用合适的模糊模型和制定适当的规则可计算出误差的大小,从而把传感器的输出校正到要求精度。

图2 模糊逻辑原理框图
根据图1实验得到的数据,其模糊逻辑规则的补偿结果如图2所示。在传感器之后接一个模糊控制器,把温度数据作为输入信号,经模糊推理得到校正后的陀螺零漂值,通常模糊控制器包括模糊化、模糊规则、模糊推理和清晰化四个过程。
模糊推理通常是基于Zadeh-Mamdani模型或Takagi-Sugeno(T-S)模型。文中选用T-S模糊模型来对温度建模,其中T-S模型表述为[8]:
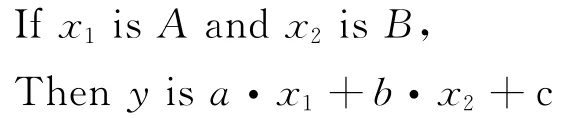
其中:A、B、C是模糊逻辑语言,a、b、c是常系数。
2.1 模糊化
借助T-S方法,建立非线性的模糊规则。为简化运算,建立一元的局部T-S模型规则:

其中:yT为在对应温度T下的陀螺零偏漂移值,T为温度变量,选取室温25℃为标准温度。b、aT为温度敏感系数。
2.2 模糊规则
制定模糊规则是建立在实验与经验的基础上的,把温度变化的论域[-40,75]划分为6个模糊子集,采用如图3所示的隶属度函数。

图3 模糊隶属度函数
根据TS模糊逻辑,跟温度T有关的第i(i=1,…,6)条规则:
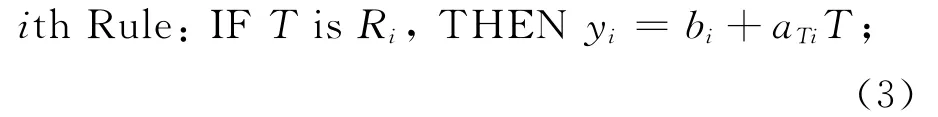
在模糊逻辑算法中,b、aT可视作线性局部模型系数,如能得到b、aT两个敏感系数,则可确定在Ri规则下的输入输出的隶属函数,即模糊基函数。文中通过重复实验数据,采用正交最小二乘法来确定隶属函数中的两个系数。
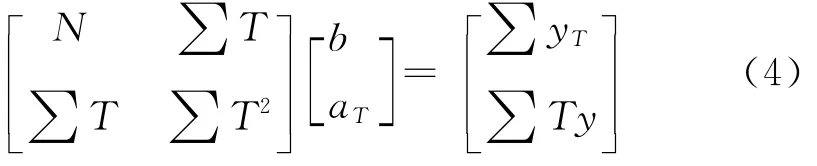
式中N表示拟合数据个数。根据测量的陀螺样本数据和温度值,可计算出某规则下的局部模型的模糊系数。由此可得到6个模糊子集的模糊规则。此六组参数可视作局部规则中的线性因子,可通过实验数据提前得到,并预存于计算机中,作为实时推理所需调用参数。
2.3 模糊推理及输出
对于输入温度值T,其模糊推理类似于与该温度有关的所有规则的插值运算,各规则根据在此温度条件下所分配权重的不同,则权重表示如图4所示。在此例中,模糊输出值为[7]:
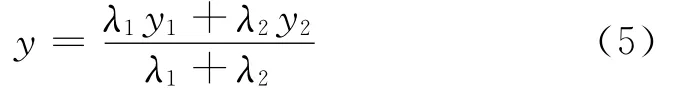
其中λi为输入变量在规则Ri上的隶属度,也可以看成是第i条规则加权因子,如温度T=-20℃时,根据图3所示规则,λ2=1,其余为零,即第2条规则在此温度输入下的权重占到最大。

图4 模糊推理
为达到实际应用的目的,将模糊集合映射为一个确定的点,这个过程称为去模糊化。文中采用重心法,由所有控制规则推理结果共同作用产生。将计算隶属度函数曲线包围区域的重心,可根据此参数得到去格式化的最终结果。
因此,对于任何输入温度T,其模糊输出可写成:
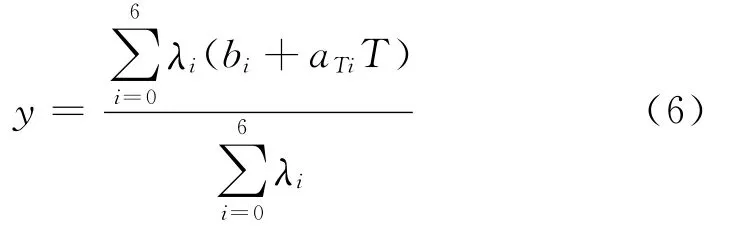
2.4 陀螺零漂补偿
对于模糊补偿模型中每个局部集合,针对每个输入温度值,跟温度相关的陀螺的零偏补偿输出结果可表示:

式中:y为陀螺原始数据,(b+aTT)为模糊补偿值,为陀螺温度补偿后的输出值。则根据式(6),经过补偿校正后的最终输出结果为:

3 实验结果分析
为验证一元T-S模糊逻辑方法在MEMS陀螺零漂温度补偿的效果,以AD公司MEMS陀螺的ADIS16355为例,辅以高速DSP处理器TMS320VC 5416为数据处理器。ADIS16355为六自由度的MIMU,取用x轴向陀螺的数据作相关分析。
首先验证陀螺较长时间工作而自身发热的温度补偿效果。将陀螺置于温控箱内,温控箱未启动,让陀螺工作2h。因封闭环境无法散热,由图5可知,陀螺的输出温度由室温25℃升至45℃,其角速度输出也有一个缓漂。
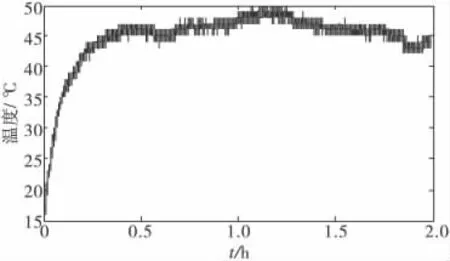
图5 陀螺自身工作的温度变化情况
图6所示为MEMS陀螺的原始输出数据和经过温度补偿后的数据。经补偿后其漂移有明显的减小。将两组数据经ALLAN方差计算,其零偏稳定性由0.0075°/s降低为0.007°/s。

图6 因自身发热的温度补偿对比曲线
调节温控箱的温度在25℃、45℃、50℃、55℃、65℃、70℃六个温度点,每个温度点采集大约为1h的陀螺数据,并同时输出原始数据和温度补偿后的数据,将各个温度点的两组数据分别用ALLAN方差计算其零偏稳定性,如表1所示。
由表1可知,在室温条件下,陀螺的零偏值跟标称值相符,在其它温度下,零漂有相应的变化,经过模糊逻辑的温度补偿后,其零偏稳定性与室温条件下一致。图7描述了其补偿前后的变化情况。

表1 MEMS陀螺零漂补偿前后
以T=65℃为例,陀螺原始数据偏离零位0.025°/s之多,而经过温度补偿后数据回归至零位附近。实验证明,此方法达到补偿效果。
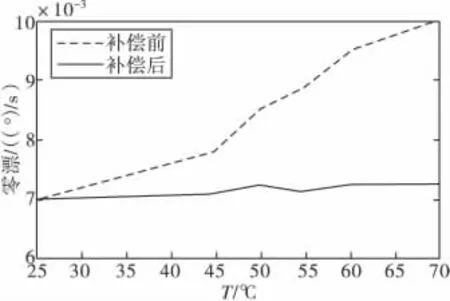
图7外界温度变化补偿前后曲线
为验证上述方法的实时性,将其与文献[2]所采用的多项式拟合方法的计算作为对比。以温度T=65℃为例,在实验中采用6次拟合多项式,通过DSP计算,将DSP的主频设为160M,用CCS3.1软件观察算法运行的指令周期数。具体对比见表2。
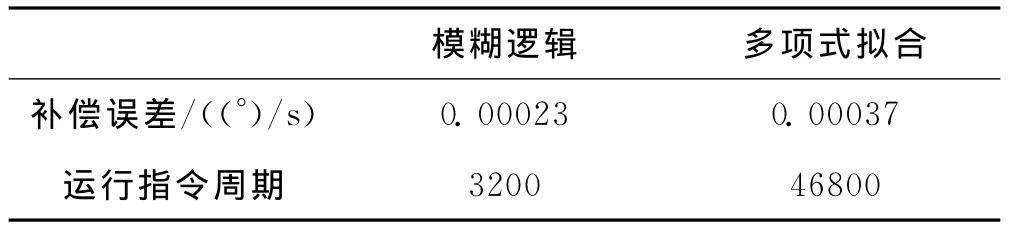
表2 算法补偿效果的比较
由表2可知,模糊补偿算法单次运行的指令周期为3200左右,而多项式拟合方法的计算指令周期为46800左右,而模糊补偿算法的补偿效果也明显好于多项式拟合方法。
4 结论
文中采用模糊推理的方法对MEMS陀螺ADIS16355进行非线性误差校正,无需建立精确的数学模型,有较强的鲁棒性和广泛的适用性。由实验结果可知,经温度补偿后的陀螺零漂显著减小。并且该方法计算简单,易编程实现,可有效的保证实时性,适合于工程应用中动态性能要求较高的场合。
[1]陈怀,张嵘,周斌,等.微机械陀螺仪温度特性及补偿算法研究[J].传感器技术,2004,23(10):24-26.
[2]程龙,王寿荣,叶甫.硅微机械振动陀螺零偏温度补偿研究[J].传感器技术学报,2008,21(2):483-485.
[3]赵晓辉,伊国兴,王常虹.硅微陀螺温度漂移补偿研究[J].传感器与微系统,2008,27(10):48-50.
[4]何晓峰,胡小平,吴美平.基于半参数回归模型的微陀螺仪温度补偿技术[J].压电与声光,2009,31(6):794-796.
[5]张红线,吴衍记,王玉辉,等.基于模糊逻辑的光纤陀螺温度补偿技术[J].中国惯性技术学报,2007,15(3):242-246.
[6]M El-Diasty,A El-Rabbany,Pagiatakis.Stochastic characteristics of temperature-dependent MEMS-based inertial sensor error[C]//The Institute of Navigation National Technical Meeting,2006.
[7]Hong KS.Compensation of nonlinear thermal bias drifts of sronant rate sensor using fuzzy logic[J].Sensors and Actuators A:Plysical,1999,78:143-148.
