具有部分缺失数据的异均值方差分析法

廖娟芬，黄绍军，李春红

（广西大学 数学与信息科学学院，广西 南宁 530004）

具有部分缺失数据的异均值方差分析法

廖娟芬，黄绍军，李春红

（广西大学 数学与信息科学学院，广西 南宁 530004）

在很多情况下，由于各种原因试验的数据都会有局部的缺失，文章提出在有部分数据缺失情况下的异均值方差分析法，并将其用于检验多个样本数据是否具有某种类型的不同均值.

缺失数据；方差分析；异均值

基于现实的数据的采集，几乎所有的抽样调查都会不同程度地受到无回答的干扰，或者所得的数据因某种原因丢失，这些数据都称为无响应.如果对缺失了的数据仍然采用完全数据的统计方法，则其分析会出现偏差，因此对于缺失数据的研究是现在学者关注的一个热点[1-3].

在文献[4]傅惠民提出了一种线性模型完全数据的异均值方差分析方法，这种异方差分析方法是检验多个总体是否具有某种不同的均值，与传统的方差分析检验均值是否相等.傅惠民还研究了关于多因子异方差分析，并将其应用到机械行业，得到了较好的结果.但是没有研究在数据具有缺失情形下的异方差分析.那么本文将给出具有部分缺失数据的异均值方差分析法.

1 引进模型

1.1 完全数据下的异均值方差分析

在文献[4]中已给出在完全数据下的异均值方差分析法，即：设因素A有a个水平，在第i个水平下做了ni次实验，试验值记为Xij,j=1,2,…,ni.且 Xij～N( )μi,σ2，其中

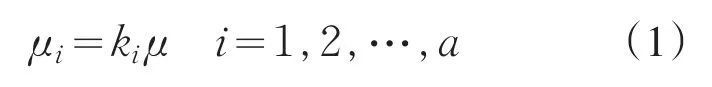
式中的μ和σ2均为未知参数.异均值方差分析主要是根据试验结果，检验由仿真、数字化设计，实验等方法求得的ki( )i=1,2,…,a 是否满足式（1），同时对未知参数μ和σ2进行估计.令

1.2 缺失数据下的异均值方差分析

假设a个总体的每个试验值是在完全随机缺失机制下以同样的概率1-p( )0＜p＜1（未知常数）被丢失，也就是说关于第i个水平的总体实际得到的试验值为

2 随机模拟

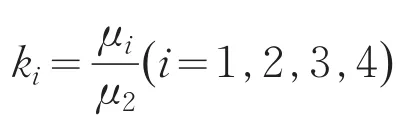
运用缺失数据的异均值方差分析对表1的数据进行处理，可得：

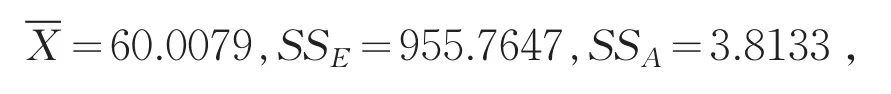
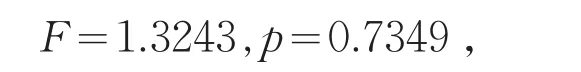
对于显著水平α=0.05,可以查表知F＜F0.05( )3 946,且 p＞α所以不拒绝原假设，也就是有（1）式成立.

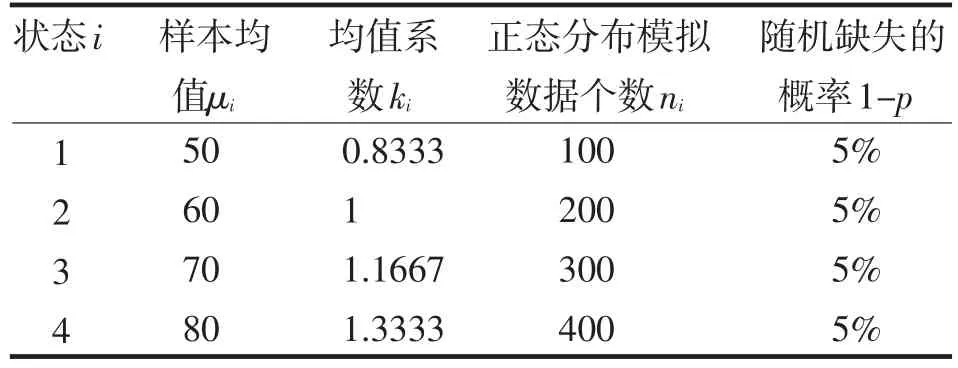
表1 用于数值计算的数据Tab.1 The data for digital computaion

若将其当成是完全数据，不考虑数据的缺失而进行分析，即运用模型1的方法进行技术，则将有下面的结果：

通过两种算法可知，本文提出的在具有缺失数据下的异方差分析是效果比较理想的.

3 结论

本文的方法能够在数据具有部分缺失情形下的仿真和数字化设计得到的均值系数进行大样本检验，并且根据试验数据对参数μ和σ2重新进行估计.

[1]王松桂,陈敏,陈立萍.线性统计模型[M].北京:高等教育出版社,2007.

[2]金勇进,邵军.缺失数据的统计处理[M].北京:中国统计出版社,2009.

[3]赵志文,赖民,宋立新,等.具有部分缺失数据的两个对数正态分布总体参数的估计和检验[J].统计与决策,2009(20):7-9.

[4]傅惠民.异方差分析方法[J].机械强度,2005,27(2):196-201.

Variance Analysis of Different Means Values with Missing Data

LIAO Juanfen，HUANG Shaojun，LI Chunhong
（College of Mathematics and Information Science，Guangxi University Nanning，Guangxi530004，China）

In many cases，experimental data may be lost locally for various reasons.This paper gives a method for analy⁃sis of variance of different mean values with partially missing data,which is used to check whether multi-populations have a certain type of different mean values.

Missing data；Analysis of variance；Different mean values

O 211.3

A

1674-4942（2011）01-0009-03

2010-11-20

毕和平