水中弹体在爆炸冲击波作用下的有限元分析
2011-12-08李凤琴李涛峰
李凤琴,李涛峰
(黄河水利职业技术学院,河南 开封 475003)
0 引言
当弹性物体(结构)在水下运行时,受到水流、波浪和冲击波等流体动力或其他非流体因素的激励,结构发生振动,其周围流场也随之改变。 流场的变化反过来又影响结构的振动。 这样层层耦合,就形成了流体—结构相互作用的流固耦合系统[1~2]。
水中弹性物体在服役期间极有可能遭受水雷、炸弹等非接触式水下爆炸武器的袭击,为了保证弹体的安全和正常使用,弹体结构必须具有一定抗水下爆炸载荷的承载能力。 弹体承受水下爆炸载荷是弹体结构在很短的时间内,在巨大冲击载荷作用下的一种复杂的动力响应过程,对其进行详细的理论研究,并试图通过建立一个精确的数学模型,使水下爆炸问题得到完全的解析是十分困难的。 而爆炸实验属于破坏性实验,实验经费昂贵、实验设备复杂,并且也不能从根本上解决这一问题。 计算机硬件和相关软件的飞速发展,使得弹体在水下爆炸载荷作用下的数值模拟成为可能。 本文试对弹体在水下爆炸冲击载荷作用下的动力响应问题进行了数值模拟,以期得到一些有用的结论。
1 理论分析
为了研究处于无限水域中的弹体在爆炸载荷作用下的动力响应,在综合考虑计算精度和计算成本的条件下,选取10 倍弹体半径的水域进行建模计算,并按照无限水域情况,对流场边界条件进行适当的处理,以消除有限计算水域带来的边界影响[3]。在有限元计算中,采用球形TNT 药包[4],炸药位于弹体轴线正左方,距离弹体轴线6 m 处,可得到迎爆面为3 MPa 压力峰值。 具体模型如图1 所示:
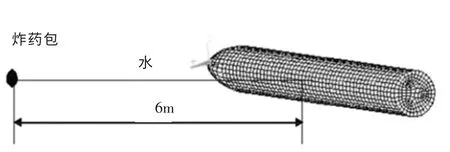
图1 弹体在水中与爆炸荷载的关系图Fig.1 Relations of missile and detonation in water
1.1 弹体瞬态分析理论[5~6]
瞬态振动研究过程实际上是求解微分方程的过程,其内部程序采用的是Newmak 法。瞬态动力学求解的运动方程为:
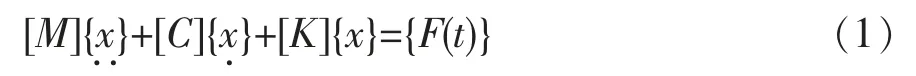
式中:{F(t)}为载荷向量(在本文中为TNT 球形药包爆炸冲击波压力),可以随时间任意变化。
1.2 爆炸载荷及流体动压力[4]
流场和弹体之间进行能量交换,极大地影响着弹体受到的载荷及其自身的响应特性。 因此,在分析弹体水下爆炸动力响应时,必须考虑弹体与流体之间的耦合作用。
在自由流场中,TNT 球形药包爆炸生成的冲击波在水中传播时,波面上的压力峰值Pm可用著名的库尔公式计算:

式中: Pm为波阵面上的压力峰值,MPa;W 为炸药重量,kg;R 为弹体壳与爆源的距离,m。
圆柱壳在水下爆炸冲击载荷作用下所受到的冲击压力P 包括3 个部分(如图2 所示),即

式中:Pe为爆炸冲击载荷,其值由Pm公式算出;Pd为液体动压力;Ph为静水压力在水深hf处的圆柱壳表面所受静水压力,为Ph=ρfghf。
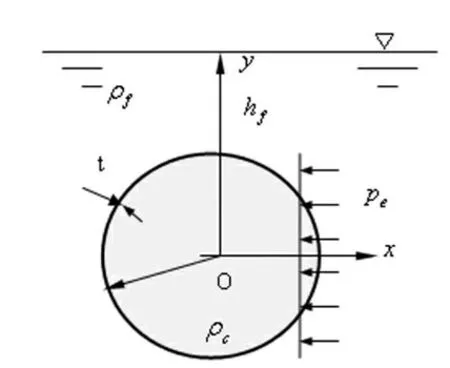
图2 弹体在水下爆炸冲击载荷作用下受到的压力图Fig.2 Stress of missile under detonation impact loads in water
2 弹体水下爆炸有限元模型的建立[7]
如图2 所示,静液流场中,一半径为r、厚度为t的弹体壳在液面下hf处受到水中爆炸冲击载荷作用。 为便于研究,在分析过程中对弹体壳、液流场和爆炸载荷有以下基本假定:(1) 弹体壳用密度为ρc的弹性线性各向同性材料;(2)流体是无黏、无旋、不可压缩的水,密度为ρf;(3)仅考虑爆炸的一次冲击波,且认为是平面波。
对弹体用solid45 单元进行剖分,单元简图如图3 所示。 实常数单元厚度设定为2 mm,为铸造铝合金材料,密度ρc=2 640 kg/m3,弹性模量E=68.6 GPa,泊松比v=0.3。对弹体周围的水,用fluid30 单元进行剖分,水的密度ρf=1 000 kg/m3,声波在水中传播速度C=1 450 m/s。
因为实体和流体单元之间已经确立映射关系,弹体表面的所有节点都与界面上的流体单元节点共享,所以耦合关系一般是直接的。 弹体与水耦合系统的有限元模型剖面图如图4 所示。 图4 中,内部网格密的部分为壳单元,有4 312 个,周围网格相对较疏的部分为流体单元, 有103 796 个, 共有122 423 个节点,所以计算量很大。
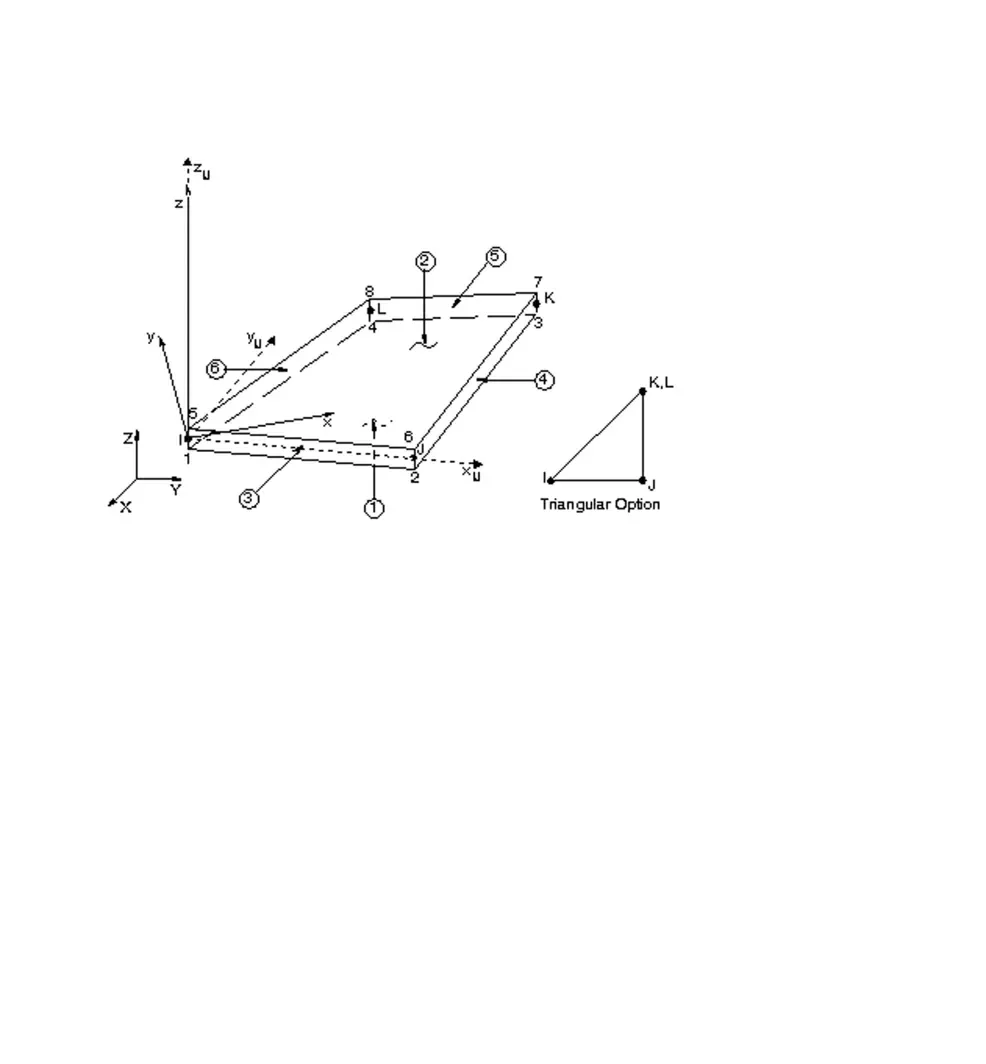
图3 弹体与水耦合系统的solid45 单元简图Fig.3 Solid45 unit graph of missile and water coupled system

图4 弹体与水耦合系统的有限元模型剖面图Fig.4 Finite element model section of missile and water coupled system
3 加载并求解
3.1 弹体在空气中和水中受到爆炸冲击载荷后响应的对比
弹体壳在爆炸载荷(Pmax=3.0 MPa)的作用下,空气中和水中的变形曲线如图5 所示。
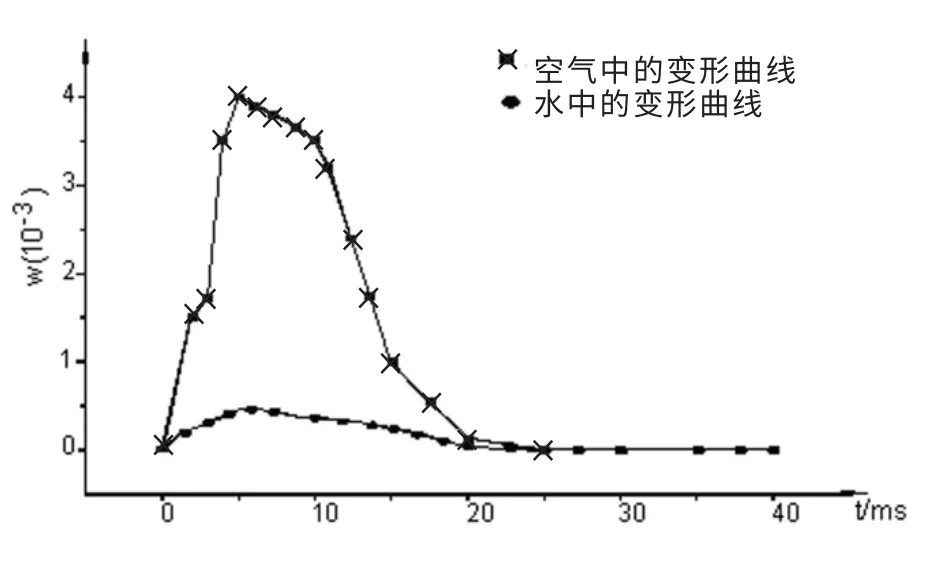
图5 弹体在水中与在空气中的变形曲线比较图Fig.5 Deformation curve comparison of missile in air and in water
从图5 可以看出,在空气中,弹体壳受到爆炸载荷作用后,纵向变形迅速增大,而水中的弹体壳受到冲击后,由于受到水阻力作用(相当于附加质量),发生的纵向变形远比空气中的要小。 这是因为,在爆炸冲击载荷作用下,静止的水流吸收了一部分爆炸冲击能量,再加上液固耦合的作用,所以弹体在水中的变形远没有在空气中的大,当然动力(运动)性能也较空气中的稳定。
3.2 弹体迎爆面上节点1467 在爆炸荷载作用下沿不同方向的变形图
弹体壳上迎爆面一节点的位移-时间历程曲线如图6 所示。
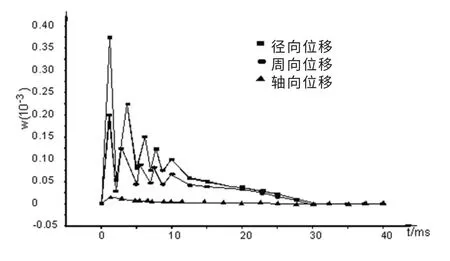
图6 弹体壳上一点u,v 和w 的时间历程曲线图Fig.6 U, v and w time course curve of one point of missile
从图6 可以看出, 壳体在3 个方向的位移都是存在的。 在曲线的起始段,位移很快增大,然后边振动边按指数规律衰减,且每条曲线的振动频率一致。因为水下爆炸冲击波的压力也是服从指数衰减规律的,径向位移最大,周向次之,轴向最小,它们以同样的频率衰减,最后稳定地趋于零。
3.3 水中弹体不同位置在爆炸荷载作用下的响应比较
在爆炸载荷(Pmax=3.0MPa) 作用下, 水面下hf=10.0 m 处的弹体不同部位的变形曲线如图7 所示。
由图7 可以看出,在爆炸初始阶段,由于迎爆面A 处节点1467 受到最大的冲击压力作用,产生较大的内凹变形,而背爆面C 处节点1586 则变形较小。接下来, 由于流体力的作用,A 处变形受到制约,B处节点4922 变形迅速增大,C 处位移仍较小。 随着冲击波传播,C 处变形也迅速增大,在流体阻力下,A和B 处位移渐渐趋于一致。
4 结语
本文基于弹体与水流场相互作用的流固耦合运动条件, 对弹体在水下爆炸冲击载荷作用下的弹性动力响应问题进行了数值模拟, 得到水下弹体在爆炸冲击载荷下弹性动力响应的规律。
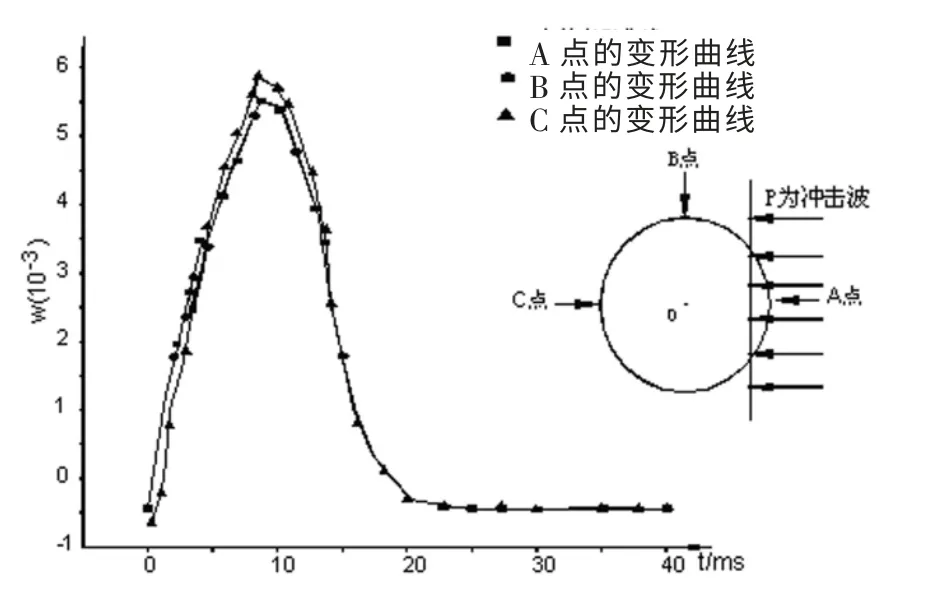
图7 水中弹体不同部位变形比较曲线Fig.7 Deformation comparison curve of different parts of missile in water
(1)在冲击载荷作用下,由于静止的水场吸收了部分爆炸冲击能量,水中弹体变形远较空气中小,动力(运动)性能也较空气中的稳定。
(2)壳体在轴向、径向、周向3 个方向的位移都是存在的,径向位移最大,周向次之,轴向最小。 它们以同样的频率衰减,最后稳定地趋于零。因此,考虑在哪个方向存在最大的位移,是保证安全设计的关键。
(3)在爆炸载荷作用下,弹体各部分(如背爆面)也会受到几乎与迎爆面一样的冲击载荷作用, 它造成的破坏作用应引起注意。
[1] 杜 颖,刘习军,贾启芬. 液固耦合动力学问题的研究[J].机床与液压,2004(11):9-12.
[2] 居荣初. 弹性结构与液体的耦联振动理论[M]. 北京:地震出版社,1983:223.
[3] 金占礼,王宗利,李红云,等. 结构在无限流体域中振动时附连水质量的计算方法[J]. 上海交通大学学报,2000,34(8):1078-1082.
[4] 周听清. 爆炸动力学及其应用[M]. 合肥:中国科学技术大学出版社,2001:108-118.
[5] 王富耻,张朝晖. ANSYS10.0 有限元分析理论与工程应用[M]. 北京:电子工业出版社,2006.
[6] 叶先磊,史亚杰.ANSYS 工程分析软件应用实例[M].北京:清华大学出版社,2003:236-270.
[7] 黄玉盈. 结构振动分析基础[M]. 武汉: 华中工学院出版社,1988:204-211.
