某火箭炮闭锁挡弹器结构设计与仿真分析＊

2011-12-07乐贵高陈学义

弹箭与制导学报 2011年5期

姜勇，杨全，乐贵高，陈学义

（南京理工大学机械工程学院，南京 210094）

0 引言

闭锁挡弹器作为定向器的一个重要组成部分，其作用是在发射前和载弹行军时将火箭弹可靠的固定在定向器的一定位置上，以防止火箭弹由于重力、燃气流作用力、振动惯性力等作用而产生移动、跳动甚至脱落掉弹，保证火箭弹与点火装置良好接触，并在发射时提供一定的闭锁力[1]。由于闭锁力的大小直接关系到行军、射击的安全性和火箭弹射击密集度，因此闭锁挡弹器设计计算的主要问题是确定闭锁力的大小。

目前火箭发射装置采用的闭锁挡弹器有三种基本形式：弹／卡簧式闭锁器、摩擦式闭锁器和杠杆式闭锁器，具体的选取应根据火箭弹和发射装置的结构来确定[1]。文中以卡簧式闭锁器为例，对某火箭炮闭锁器进行结构设计和仿真分析。针对该火箭炮特点确定闭锁器的相关结构尺寸，分析不同预紧量下闭锁器的约束力和不同卡簧厚度下闭锁器的约束力，并且研究了闭锁力对火箭炮动态特性影响。最终确定该火箭炮闭锁器的结构尺寸。

1 闭锁力的确定

设火箭发射装置行驶在坡度度为零的道路上，在铅垂线振动和纵向角振动存在的情况下进行制动。以位于发射装置纵对称平面内的火箭弹为研究对象，火箭弹受力如图1所示。忽略摩擦力时，弹所受的实际力有：重力G；闭锁力Fb，它平行于弹轴ξ；定向器对弹定心部的支反力的合力FN，它垂直于弹轴ξ。图中o′为火箭弹质心，l′o＝o′cb，θo＋η为行军时定向器轴线x1（它与弹轴ξ重合）的仰角，而θo为行军固定状态（静态）定向器轴线的仰角。

应用动静法，得各力在弹轴ξ上投影的平衡方程：

图1 确定闭锁力示意图

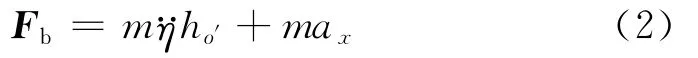
对于轮式自行火箭发射装置，η··的最大值9～13rad／s2；在坡度角等于零的情况下，ax的最大值0.8g。因此在此情况下火箭弹出现最大惯性力时所需的闭锁力为：

根据上边的理论公式可初步确定该火箭炮所需的闭锁力为1500N。

2 卡簧式闭锁器结构参数的确定

在行军制动时的惯性力、燃气流作用力及弹重力等作用下使火箭弹移动并带动定向钮作用在闭锁器上，卡簧片的弹力须抵消这些作用力以保证火箭弹的安全性。点火后，在火箭弹定向钮作用下，迫使卡簧张开，火箭弹挣脱闭锁器的约束而发射出去。卡簧式闭锁器的平面结构如图2所示。

图2 卡簧闭锁器结构

为了更好的确定该火箭炮闭锁挡弹器结构尺寸，参考原有火箭炮闭锁器结构尺寸和该火箭炮特点初步确定该火箭炮闭锁器部分结构尺寸（如表1所示）；再根据某火箭炮所受的闭锁力计算出卡簧片的厚度。其中r1和r2分别为卡簧和定向钮相接触的工作面圆弧和定向钮半径；h1和l1为给定点位置长度；b1为卡簧截面宽度；α1为斜面角。

表1 闭锁器部分结构尺寸参数（单位mm）

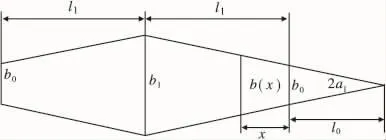
图3 卡簧宽度变化示意图

起始瞬间楔入角β0为：

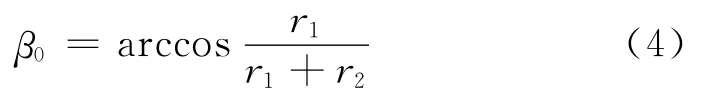
l1的变化量很微小，因此取平均值lav代替l1。

卡簧端部截面宽度变化参数（如图3所示）：

闭锁器的结构参数H、B：

卡簧厚度：

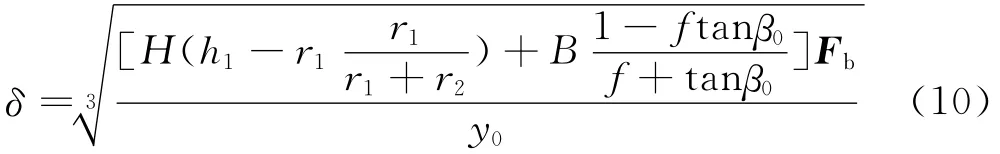
取预紧挠度y0＝3mm、f＝0.15；根据上述理论公式可以得出卡簧的厚度δ为4.1mm。但上述应用理论所计算出来的结构参数只能作为初始设计数据，而不能确定闭锁器的最终结构尺寸。以往是通过多次实验反复修改闭锁器结构参数以达到设计要求。随着结构动力学仿真软件的发展，现在可以通过计算机仿真来设计和校核。

3 闭锁器非线性动力学有限元分析

为了建立结构动力学模型，首先根据所设计的闭锁器结构参数用SolidWorks软件建立该卡簧闭锁器三维实体模型。然后利用ABAQUS软件采用减缩积分实体单元（C3D8R）对该火箭炮进行了网格划分，其网格模型如图4所示。另外，在设置火箭弹发射分析步之前要保证定向钮与闭锁器预接触，否则在火箭推力作用下很小的简隙都会使定向钮与闭锁器相碰撞而发生振荡，这样会导制起始段模拟计算不准确。所以在施加火箭发动机推力前，建立了分析步来使定向钮与卡簧之间产生接触。基于动力学理论，运用显式时间积分算法对所建模型进行仿真分析。

图4 闭锁器网格模型

3.1 在不同卡簧厚度下的闭锁力分析

利用所建立的有限元模型，取预紧量y0为2mm，分别对五种不同厚度δ的卡簧闭锁器进行仿真分析，其计算结果如表2所示。

表2 不同厚度下闭锁器的闭锁力

3.2 不同预紧量下的闭锁力分析

同样利用所建立的有限元模型，取卡簧厚度δ为4.1mm的闭锁器，分别对六种不同的预紧量y0的情况进行仿真分析，计算结果如表3所示。

表3 不同预紧量下闭锁器的闭锁力

在不同卡簧厚度和不同预紧量的各种情况下，闭锁力的变化趋势大致相同。以卡簧厚度为4.1mm、预紧量y0为2mm情况为例，闭锁力的变化规律和定向钮挣脱闭锁器约束分别如图5、图6所示。

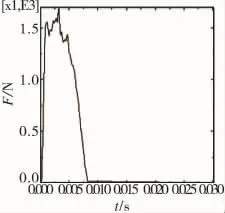
图5 闭锁力曲线

图6 定向钮挣脱闭锁器示意图

分析以上图表可得，在定向钮挣脱闭锁器约束的瞬间，闭锁器上的约束力突然增加；但这不能代表闭锁器的有效闭锁力。因为定向钮挣脱闭锁器约束的瞬间属于临界时刻，可设定这时刻的闭锁力是闭锁器的最大约束力。在这个时刻之前火箭弹在弹轴方向上发动机燃气流推力和闭锁力的合力接近于零，可认为是有效闭锁力。由表2～表3可知闭锁力随着预紧量和卡簧厚度增加而增大。厚度增加0.1mm，闭锁力增加179.25N；预紧量增加0.1mm，闭锁力力增加63.92N。因此可知闭锁力对预紧量的敏感度低于卡簧厚度。

4 闭锁力对火箭炮动态特性影响研究

建立该火箭炮结构动力学模型，选定卡簧厚度为4.1mm闭锁器并将其合理地装配在定向装置上。不考虑火箭弹质量偏心和推力偏心因素，射角为50°，闭锁器取四种不同预紧量情况下对火箭炮进行仿真分析，所得火箭炮动态响应结果如表4所示。

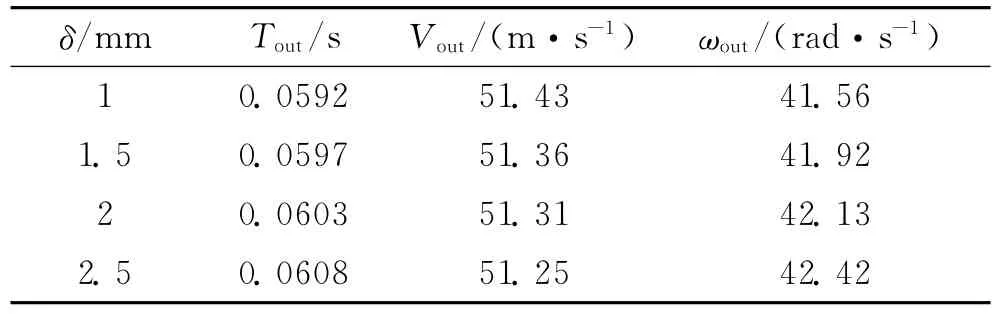
表4 不同闭锁力火箭炮的动态响应结果

在点火发射之前，对闭锁器加上一定预紧量，经历一个发射周期，其闭锁器取1mm、1.5mm、2mm、2.5mm的预紧量时定向管口振动位移曲线如图7～图10所示。在闭锁力不同的情况下，前6ms定向管口振动位移只有细微的不同，因为闭锁器的突加力对重达几吨的发射装置产生的影响会很小；因此在强大的燃气流作用下，炮口的振动位移曲线几乎一致。因此可知燃气流冲击力对火箭炮振动响应的影响比闭锁力所产生的影响大得多。在燃气流冲击力作用完之后，发射装置处于自由振动状态，它们的最大振幅出现了较小的差异，这种差异在后续发射过程中将会扩大。

图7 偏航方向角位移

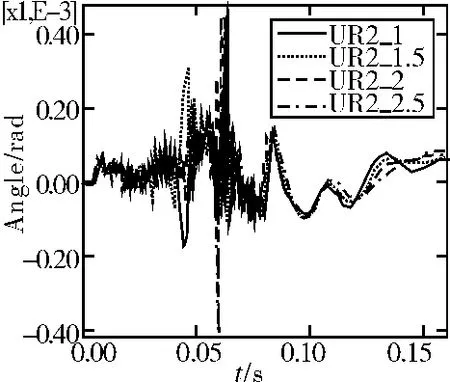
图8 俯仰方向角位移

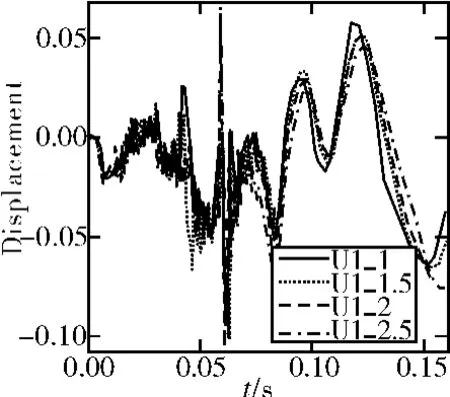
图9 偏航方向线位移

图10 俯仰方向线位移

通过上述四种不同闭锁力作用下的发射过程的仿真分析，可知闭锁力对发射装置振动影响并不明显。因为闭锁器所产生的力相对燃气流、火箭弹推力和系统重力较小，闭锁力相对小，作用时间短，对系统的振动影响不大。在满足火箭弹出定向管口的线速度、角速度和行军安全性等要求下，应使闭锁力小一些。因此该火箭炮应该选择卡簧厚度4.1mm、预紧量2mm的闭锁器。