路基土回弹模量湿度调整系数预估研究

林小平，李兴华，凌建明，周 亮

（1.交通运输部科学研究院，北京100029；2.交通运输部规划研究院，北京100028；3.同济大学道路与交通工程教育部重点实验室，上海201804）

路基回弹模量是路面结构设计的重要参数之一，湿度又是影响路基回弹模量最重要的自然因素.在我国公路设计中普遍采用最佳含水量状态下的回弹模量作为表征路基性能的重要参数，然而受地下水位升降、大气降水与蒸发、路面结构透水等因素的影响，路基湿度在使用期内会逐渐发生变化.路基在建成运行后，路基含水量会由压实时的最佳含水量逐渐达到平衡含水量，此时路基回弹模量值会发生较大变化，即路基使用状态的回弹模量与设计状态的回弹模量不一致.因此，有必要对路基土回弹模量湿度调整进行深入研究，以便能为路面结构设计提供科学准确的参考值.

本文在分析总结国内外有关路基回弹模量与湿度关系的研究基础上，选取回弹模量湿度调整系数模型，通过室内三轴试验，测试不同土组在不同湿度状况下的回弹模量值，建立符合我国粗细粒土组的湿度调整系数预估模型，最后推荐了回弹模量湿度调整系数值，以预估不同湿度状况下路基土的回弹模量.

1 路基土回弹模量—湿度关系

研究表明［1］，路基土回弹模量受物理状况、应力状况和材料性质等因素的影响，其中含水量（饱和度或湿度）是主要影响因素，即路基土回弹模量随含水量的改变产生较大变化.国内外很多学者对路基土回弹模量与含水量间的关系展开了试验研究［2－5］，采用回归统计方法建立了试验用土的回弹模量与含水量的关系，然而由于试验过程中仅针对了某种特定应力状态或某种特定土类，因此各模型的适用范围受到较大限制.

Li与Selig［6］针对影响路基土模量的因素进行深入分析.采用归一化的方法将所有影响回弹模量的因素转化为最佳含水率与最大干密度条件下的参考模量值，从而降低了除含水率以外的其他因素对回弹模量的影响，建立了如下的回填模量调整系数模型：

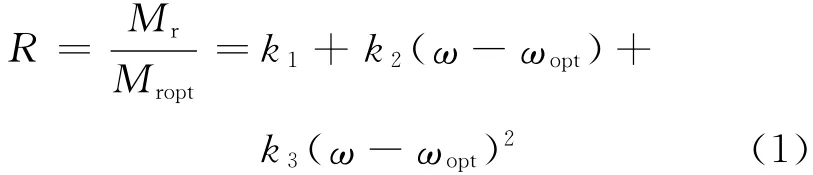
式中：Mr为实际含水率条件下的回弹模量；Mropt为最佳含水率条件下的回弹模量；ω为实际含水率；ωopt为最佳含水率；k1，k2，k3均为回归系数.

Drumm 等［7］同样将最佳含水率状态下的回弹模量做为参考值，依据室内试验测得的回弹模量与饱和度值，建立了如下的模量调整模型：

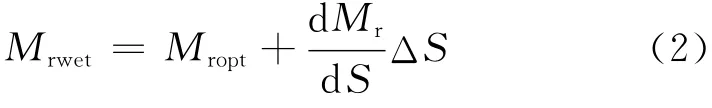
式中：Mrwet为压实后土的回弹模量值；Mropt为最佳含水率和最大干密度下回弹模量值；ΔS为压实土饱和度的变化；dMr／dS为回弹模量与饱和度变化曲线的斜率.

Drumm 认为土的饱和度S同时反映了土的湿度与密度状况，因此较含水率ω更适用于作回弹模量的预估变量.但该模型仅适用于偏湿（高于最佳含水率）状态下预估土的回弹模量，而不能预估偏干状态时的模量值.

Witczak等［8］通过对已有文献数据进行分析，发现在半对数坐标系统中，回弹模量与湿度之间大致呈线性关系，提出如下的回弹模量调整模型：

式中：Mr为当饱和度为S时的回弹模量；Mropt为在最大干密度和最佳含水率条件下的回弹模量；Sopt为最大干密度条件下的饱和度；ks为材料参数.

Witczak 等［9］对LTPP（long－term pavement performance）10个季节性观测路段（SMP）路基湿度的监测数据进行分析，结果表明大多数基层和底基层材料的湿度很低，其饱和度仅为3%～10%，较最佳含水率条件下的饱和度下降约50%.为此，推荐采用保守外插法，建立了如下的模量调整模型：

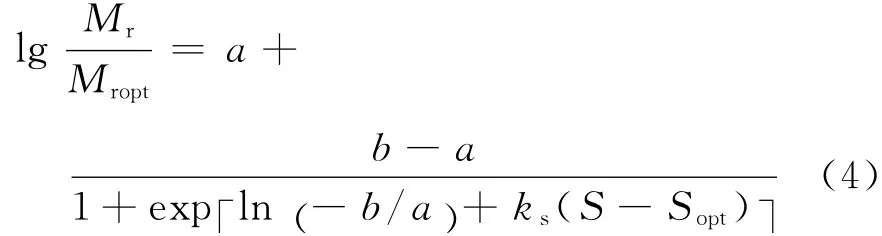
式中：a为lg（Mr／Mropt）的 最 小 值；b为lg（Mr／Mropt）的最大值；其余符号同前.

国内外提出的众多回弹模量与湿度关系式中，Witczak提出的式（4）所示的调整系数预估模型已通过大量室内试验与LTPP－SMP观测数据验证.该模型无论是针对细粒土还是粗粒土，当采用饱和度作为自变量时，其模量结果覆盖范围广且均匀，具有较强的可延展性，更主要的是在实际道路使用过程中路基湿度较易测试，为模型验证与应用提供了良好的基础数据.故本文通过室内三轴试验结果对Witczak模型进行验证与校正，推荐符合我国不同土组的路基土回弹模量湿度调整系数，为路基模量的合理取值及路面结构分析提供可靠参数.

2 室内回弹模量试验方案

2.1 路基土基本物理性质参数

按照我国公路工程路基土分类标准，分别选取了几种最具代表性的土，材料出自几处实体工程，几种路基土的物理性质参数见表1.

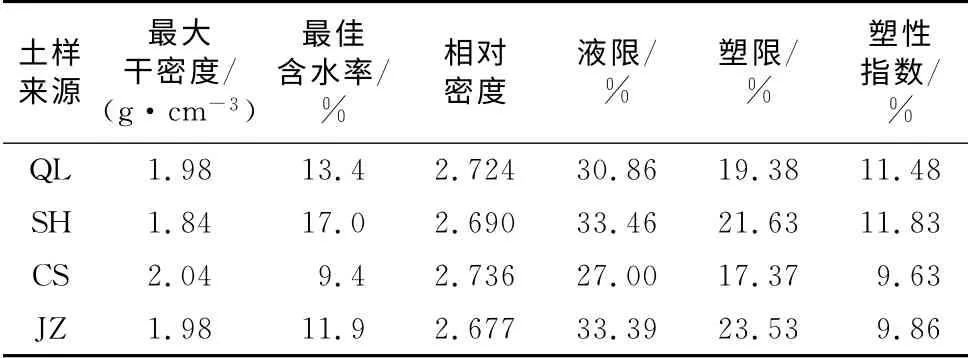
表1 路基土的物理性质参数Tab.1 Basic properties of soils

2.2 回弹模量试验

目前，重复加载三轴试验是测试路基土回弹模量的首选方法.本文参照美国AASHTO（American Association of State Highway and Transportation Officials）路基土与未处理粒料回弹模量试验规程（AASHTO T292—91），结合我国路面结构的实际状况和试验仪器情况制定了重复加载三轴试验方法.试验仪器为澳大利亚产通用测试仪UTM－100，围压为气压加载；试件尺寸为10cm×20cm，采用万能液压试验机静压压实成型；根据击实试验结果，分别按91%和96%的目标压实度、最佳含水率及最佳含水率加减3%与加减5%等水平制备试件；荷载形式为半正弦波，频率1.0Hz，加载时间0.2 s，间歇时间0.8 s.

3 试验结果与分析

3.1 回弹模量测试

3.1.1 土样编号与分类

腹膜反折悬吊方法为手术提供了较好的手术视野，便于手术操作，15例患者后腹腔镜下肾部分切除术均顺利完成。围手术期资料见表1，平均手术时间为（88.9±24.5）min，平均肾热缺血时间为（21.4±4.6）min，平均术中出血量为（72.0±16.6）mL，平均术后住院时间为（6.9±1.2）d，术中、术后均未输血，均未发生任何重大手术并发症。

为方便表述，本文规定试验用土样采用如下编号规则：第1个符号为土样来源地；第2个符号为目标压实度，即QL－96表示土样出处为QL 的目标压实度为96% 的土.依据《公路土工试验规程》（JTG E40—2007）中土的工程分类方法，本文将试验用土分为粗粒土与细粒土2类.

3.1.2 模量结果与分析

通过室内三轴回弹模量，得到几种土样在不同含水率状况下试件模量值，如图1所示.

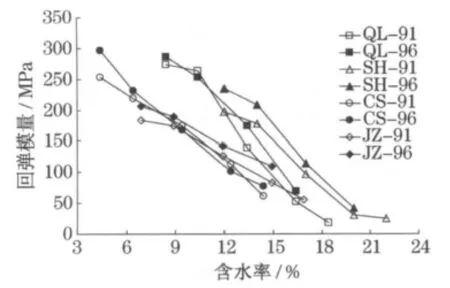
图1 土样回弹模量与含水量关系曲线Fig.1 Relationships between resilient modulus and moisture content

可以看到，无论何种土样，当压实度固定时，随着含水率的增加，回弹模量值急剧下降，不同类型土的回弹模量对含水率变化敏感程度不尽相同［1］.各类土含水率由ωopt－5%升至ωopt时，其回弹模量值均降为原模量50%左右.QL－91含水率由ωopt－5%变为ωopt＋5%时，其模量值仅为原来的6%，此含水量状况下，QL－96已达饱和状态，测试过程试件变形过大，无法测得回弹模量值.可见，湿度对于各类路基土回弹模量影响十分显著，根据路基实际湿度状况进行模量调整则凸显出其重要性.

3.2 湿度调整系数参数标定

在标定湿度调整系数的参数时需要利用试验数据进行回归拟合，若试验数据量过少，回归得到的参数值代表性则较差.由于试验用土种类与试验样本量的限制，本文仅将室内试验结果按照粗粒土与细粒土进行划分.结合室内试验结果与文献调研结果，最终取得156组细粒土有效数据，133组粗粒土有效数据，取其中部分数据进行回归分析，剩余数据进行模型可靠性验证.进行回归分析时首先需要假设最大模量比，本文参考AASHTO 2002设计指南，对于细粒土和粗粒土，假定最大模量比分别为2.5和2.0，采用Witczak模型预估的细粒土和粗粒土回弹模量调整系数与饱和度差值之间的关系如图2所示.

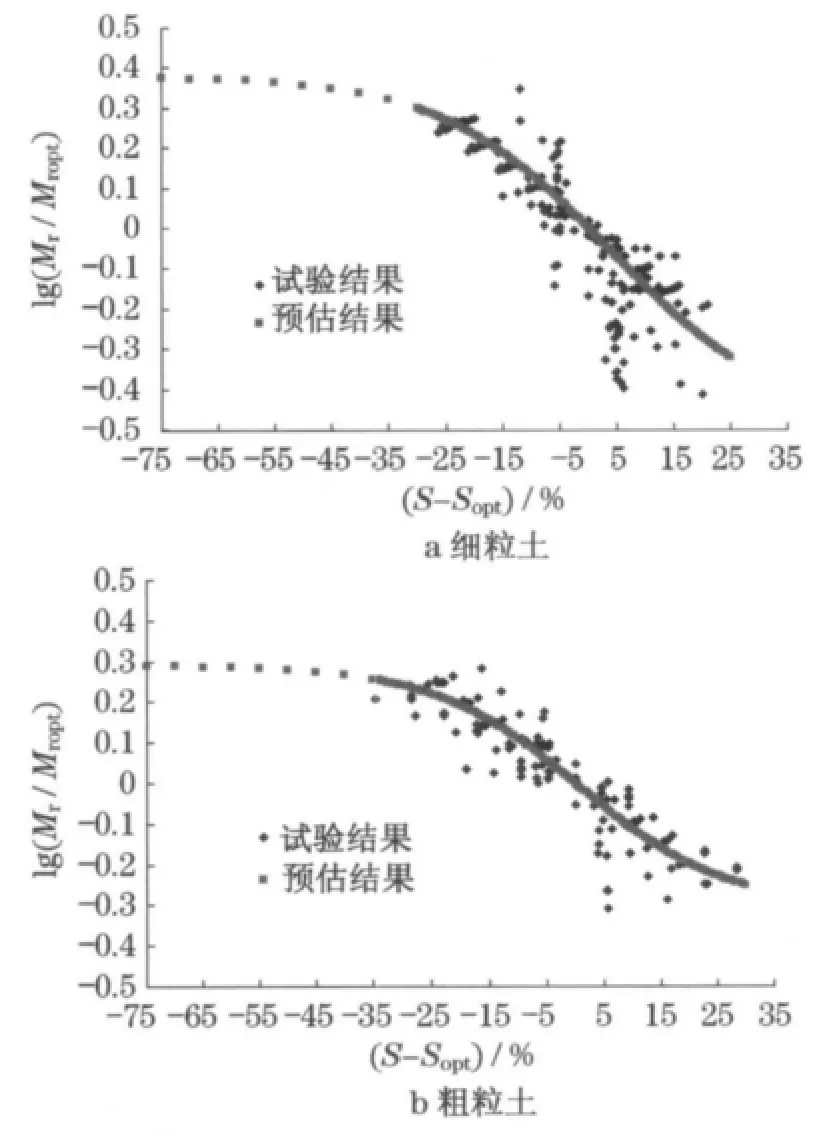
图2 回弹模量与湿度之间的关系Fig.2 Variation of modulus with degree of saturation

由图2可知，路基土湿度在最佳含水率饱和度±20%区间内，模量调整系数与饱和度差值近似呈线性关系，而当湿度比最佳含水率饱和度低20%以上时，模量调整系数受饱和度变化影响很小.在非饱和土力学中认为［9］，当土的湿度下降至某水平后，湿度对该类土强度和刚度的影响将不断减弱.本模型的预估结果与该结论相吻合.对于细粒土和粗粒土，采用室内三轴试验结果进行回归，最后综合文献数据进行回归分析，得到的模型参数a，b和ks如表2所示.

表2 调整系数回归参数结果Tab.2 Results of parameters of adjustment factor

将表2中参数分别代入式（4）中，得到如下细粒土和粗粒土的回弹模量预估模型：

由a，b的取值与回归结果可知，在最大模量比b取定之后，回归得到的最小模量比a差异甚小，说明试验测试结果与文献数据变化趋势相同，可以将此数据进行统一处理，以弥补试验数据量不足的缺点.

试验数据回归得到的ks值较大，主要是因为在进行室内回弹模量试验时含水率变化范围为最佳含水率±3%，相应饱和度变化范围为58%～93%.另一方面，部分试件当含水率超过3%时，试件难以成型或测试时由于变形量过大难以测得有效数据，故本文未能测试更多含水率条件时的回弹模量值.

对上述预估模型参数回归分析结果进行方差检验，如表3所示.图3为模型的预估结果和室内三轴试验测试结果的比较.可以看到，本文回归所得结果非常显著，可以用于校正湿度调整系数，同时，图3显示出预估模量值与实测值分布于等值线两侧，表明预估模型可靠.

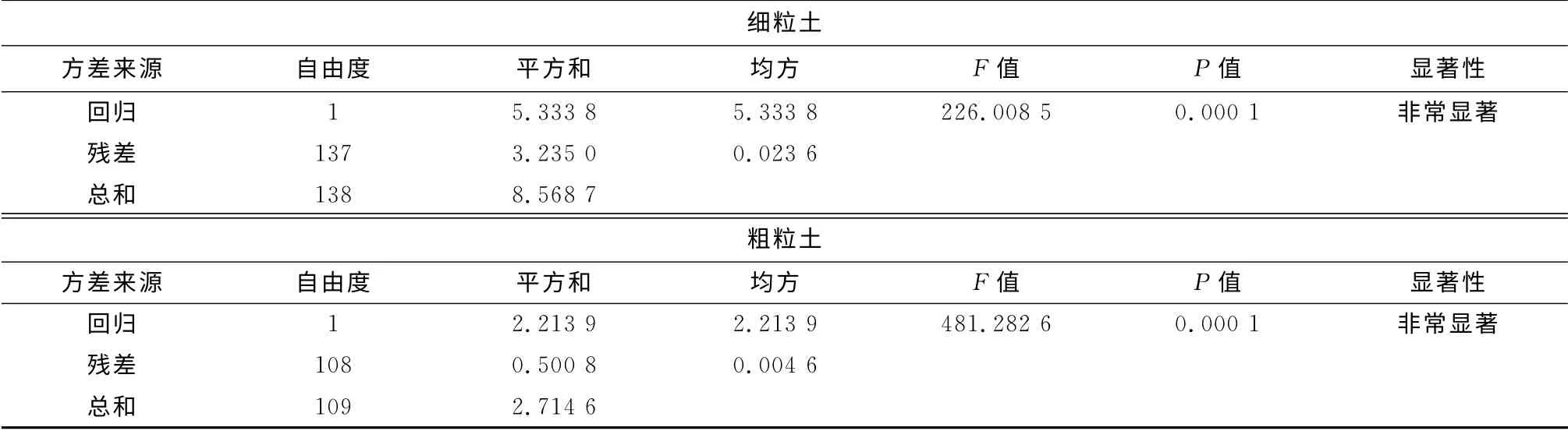
表3 路基土湿度调整系数回归方差分析结果Tab.3 Results of analysis of variance of moisture adjustment factor of subgrade

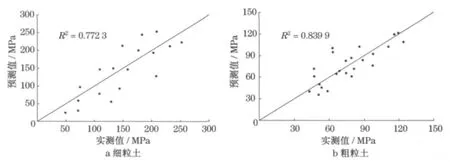
图3 回弹模量预测值与实测值关系图Fig.3 Comparison between predictive modulus and measured modulus

3.3 湿度调整系数推荐值

按不同的饱和度分别对细粒土和粗粒土回弹模量调整系数进行预估，得到回弹模量调整系数推荐值，如表4所示.需要说明的是，根据室内试验实测结果认为，该回归模型中饱和度差值常用区间为±20%.

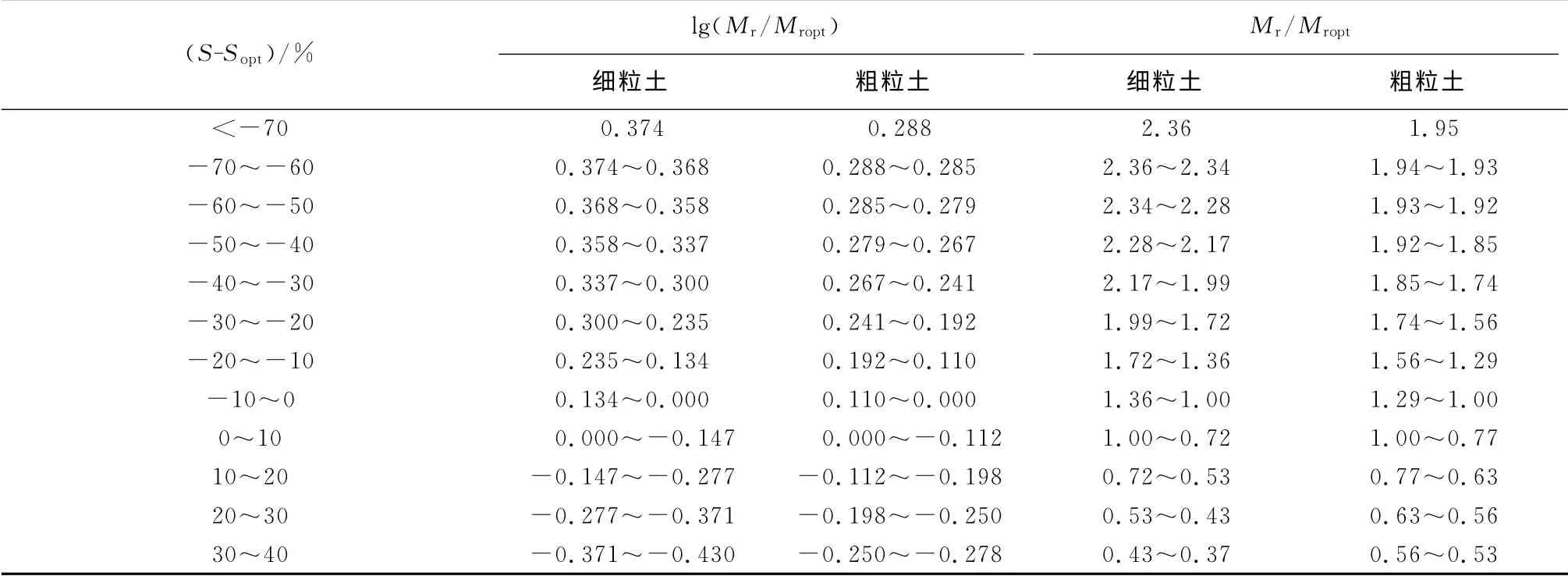
表4 回弹模量湿度调整系数推荐值Tab.4 Results of moisture adjustment factor for resilient modulus

在实际应用回弹模量调整系数时，可以根据实测路基湿度计算得到该路基实际饱和度.利用本文推荐的回弹模量湿度调整系数推荐值范围，采用线性插值方法得到该路基模量湿度调整系数，并结合室内模量测试结果，反算得到该路基实际回弹模量值，进而分析路基路面结构力学响应［10］.

4 结论

（1）路基土随着含水量的增加，回弹模量急剧下降，有必要根据路基土的实际湿度对其回弹模量进行调整.

（2）路基土湿度在最佳含水率饱和度±20%区间内，模量调整系数与饱和度差值近似呈线性关系，而当湿度低于最佳含水率饱和度20%以上时，模量调整系数受饱和度变化影响很小.

（3）对推荐的回弹模量湿度调整系数模型中的参数进行了校正，建立了适用于我国粗细粒土组的湿度调整系数预估模型，并通过方差检验和室内测试结果对比分析，表明预估模型合理可靠.

（4）推荐了不同土组回弹模量湿度调整系数值，可结合室内模量测试结果，反算路基实际湿度状况下的回弹模量值.

（5）受土组种类与室内试验样本数量的限制，本文所推荐的粗粒土与细粒土两类路基土回弹模量的湿度调整系数，其适用范围为最佳含水率饱和度±20%区间.在下一步研究中还应增加试验样本数量并细化土组划分，从而提高模型的精度，扩大其适用范围.

［1］ 凌建明，陈声凯，曹长伟.路基土回弹模量影响因素分析［J］.建筑材料学报，2007，10（4）：446.LING Jianming，CHEN Shengkai，CAO Changwei.Analysis of influence factors on resilient modulus of subgrade soils［J］.Journal of Building Materials，2007，10（4）：446.

［2］ Jones M P，Witczak M W.Subgrade modulus on the San Diego test road［J］.Journal of the Transportation Research Board，1977，641：1.

［3］ Rada G，Witczak M W.Comprehensive evaluation of laboratory resilient moduli results for granular material［J］.Journal of the Transportation Research Board，1981，810：23.

［4］ Jin M S，Lee K W，KovacsW D.Seasonal variation of resilient modulus of subgrade soils［J］.Journal of Transportation Engineering，1994，120（4）：603.

［5］ Santha B L.Resilient modulus of subgrade soils：comparison of two constitutive equations［J］.Journal of the Transportation Research Board，1994，1462：79.

［6］ Li D Q，Selig E T.Resilient properties of fine－grained subgrade soils［J］.Journal of Geotechnical Engineering：American Society of Civil Engineers，1994，120（6）：939.

［7］ Drumm E C，Reeves J S，Madgett M R，et al.Subgrade resilient modulus correction for saturation effects［J］.Journal of Geotechnical and Geoenvironmental Engineering，1997，123（7）：663.

［8］ Witczak M W，Houston W N，Andrei D.Resilient modulus as function of soil moisture：a study of the expected changes in resilient modulus of the unbound layers with changes in moisture for 10 LTPP sites［R］.Tempe：Arizona State University. Department of Civil and Environmental Engineering，2000.

［9］ Fredlund D G，Rahardjo H.Soil mechanics for unsaturated soils［M］.Ottawa：John Wiley ＆Sons Inc，1993.

［10］ 林小平，凌建明，官盛飞，等.水泥混凝土路面路基应力水平分析［J］.同济大学学报：自然科学版，2010，38（4）：545.LIN Xiaoping，LING Jianming，GUAN Shengfei，et al.Analysis on stress level of subgrade under cement concrete pavement［J］.Journal of Tongji University：Natural Science，2010，38（4）：545.