螺旋沟槽单螺杆挤出机中固体段压力分布研究

潘 龙,贾明印,薛 平,金志明,唐广利

(北京化工大学机电工程学院,北京100029)

螺旋沟槽单螺杆挤出机中固体段压力分布研究

潘 龙,贾明印,薛 平＊,金志明,唐广利

(北京化工大学机电工程学院,北京100029)

通过在固体输送段机筒内壁开设螺旋沟槽,同时将嵌入机筒沟槽与螺杆螺槽中的物料视为固体塞,建立了一个机筒与螺杆对物料协同作用的整体系统。充分考虑固体塞运动过程中的可压缩性及其受到的加速度的影响,建立数学模型,进而求解固体塞的压力及速度方程式。结果表明,固体塞在沟槽螺棱与螺杆螺棱的共同推力作用下正位移输送时,系统建压能力被显著提高,在固体输送段末端产生的沿螺杆轴向上的压力峰值有效保证了物料的稳定挤出。

单螺杆挤出机;固体输送;螺旋沟槽;压力分布;双螺棱推动

0 前言

单螺杆挤出机固体输送段的性能无论是在提高挤出过程的稳定性及挤出产量,还是在降低挤出机的比能耗方面都起着至关重要的作用,因此一直以来对于固体输送理论的研究都受到了足够的重视。目前,有关单螺杆挤出机固体输送的经典理论多以光滑机筒为研究对象,其典型代表有:Darnell和Mol提出的固体摩擦拖曳流动理论;Chung提出的黏性牵附理论;Tedder提出的能量平衡理论;朱复华等[1]提出的非塞流理论。20世纪70年代德国亚琛工业大学塑料加工研究所首先提出了具有强制输送能力的IKV挤出机,这一理念的提出为单螺杆挤出机带来了很大的发展,随后许多研究人员[2-5]相继研究了IKV挤出机的压力分布、产量、能耗等。但不论是Darnell-Mol理论还是 IKV强制输送理论,都仍旧以摩擦拖曳理论为依托来研究固体输送段的建压机理。

本文通过在固体输送段机筒内壁开设螺旋沟槽,同时将嵌入机筒沟槽与螺杆螺槽中的物料视为固体塞,建立了与Darnell-Mol不同的新型物理模型——弧板模型[6],并求解相应数学模型,弥补了Darnell-Mol理论及其他传统理论的缺陷:(1)固体塞运动过程中,忽略加速度的影响;(2)假定固体塞运动过程中密度恒定;(3)假定固体塞运动过程中输送角恒定;(4)假定固体塞速度大小恒定;(5)固体输送段初始压力不能为0。

前面研究[6]中笔者建立了以嵌入机筒沟槽与螺杆螺槽中的整体物料为固体塞、基于正位移输送机理下的弧板模型,本文将对其固体输送段建压机理进行深入研究。

1 固体输送段建压方程式

在基本假设中,我们假设压力只是沿螺槽 Z向的函数。因此取螺槽中固体塞部分进行受力分析,求解固体输送段建压方程式。

1.1 连续性方程

根据前面研究中的假设[6]可知,物料颗粒之间相互接触,在输送过程中,颗粒之间挤压导致颗粒间隙不断减小,因此可认为物料密度是不断增大的。从图1可以看出,在螺槽中沿物料的挤出方向取一个微元体,则单位时间内在沿着物料挤出方向上,流入质量、流出质量及单位时间内微元在z向上的累积量分别为:

根据质量守恒定律可得到化简后的连续性方程,如式(1)所示。根据前人研究得到固体塞压力与密度的关系如式(2)所示。将式(2)代入式(1)化简后得到式(3)。

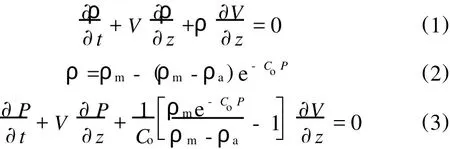
式中 ρm——极限压力下密度,kg/m3

ρa——松密度 ,kg/m3

Co——原料物性参数

P——固体塞压力,M Pa

V——固体塞速度,m/s

1.2 运动方程

图2为图1中微元的受力分析图。由微元在逆螺棱和顺螺棱方向上受力平衡求解得到化简后的运动方程 ,如式(4)所示。

图1 微元的运动分析Fig.1 Diagram of motion analysisof element

图2 微元的受力分析Fig.2 Diagram of force analysis of the element

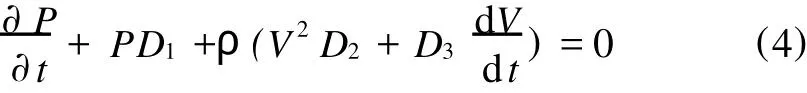
1.3 模型求解

无量 纲式:

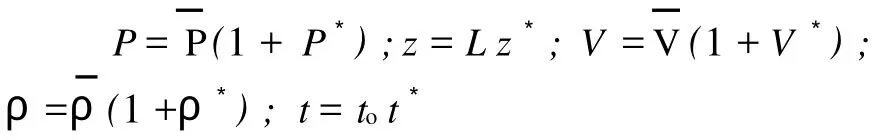
无量纲边界条件为:

无量纲初始条件为:

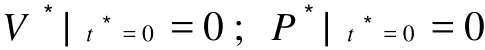
对连续性方程和运动方程进行无量纲化及线性处理、Lap lace变换、Lap lace终值定理和有量纲化求解后得到固体塞压力 P和速度V的表达式,如式(5)所示。其中 Di的表达式如式(8)～(16)所示,未注明参数均同于文献[6]中参数注释。

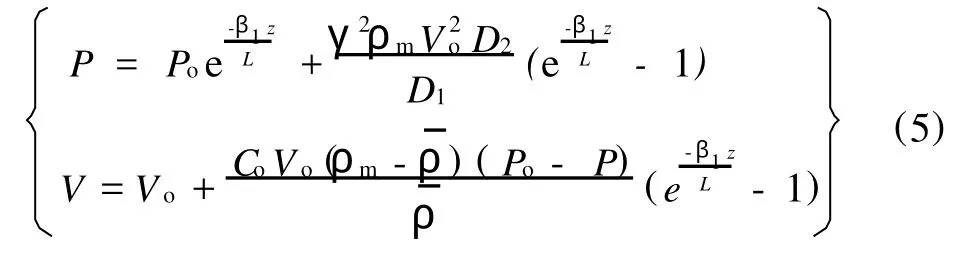
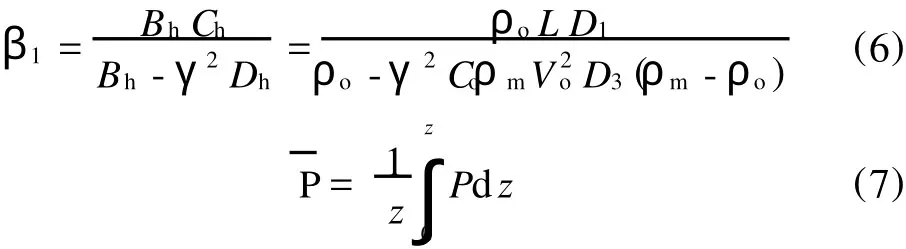
式中 z——沿螺杆螺槽方向距离,mm

γ——修正因子

WS1——螺杆根径处槽宽,mm

Wb1——螺杆顶径处槽宽,mm

Di——与机筒、螺杆结构参数及摩擦因数有关

2 结果与讨论

本文以燕山石化生产的牌号为LD607的低密度聚乙烯(PE-LD)为原料,其物性参数如表1所示。螺杆加料段几何结构参数如表2所示。

表1 LD607的物性参数Tab.1 Physical properties parameters of LD607

表2 螺杆加料段的几何结构参数Tab.2 Geometric parametersof screw feeding section

开槽挤出机加料段沟槽数N的取值与螺杆直径D是密切相关的[7]。对于大螺杆直径挤出机通常取 N≈D/10;而当螺杆直径减小时沟槽数应增多,尤其对于小螺杆直径的挤出机更是如此,通常取 N≈D/5。Potente[8]研究发现,实际应用中沟槽总宽(B)应满足:D≤B≤0.5πD。而为了使机筒平均摩擦因数达到最大值的95%,则应满足:

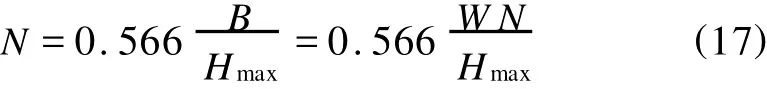
式中 W ——沟槽宽,mm

B——沟槽总宽,mm

N ——沟槽数

Hmax——最大沟槽深,mm

本文中,螺杆顶径 Db1=45 mm,沟槽数 N=8,沟槽宽 W2=8.0 mm,则 B=64 mm,Hmax=4.52 mm,取沟槽深 H2=2.5 mm。研究表明[9],在相同的沟槽几何结构参数下,沟槽螺旋角θ在40°～60°之间时产量达到最大,如图3所示。参照文献[9]中实验研究模型及文献[6]中基于正位移输送边界条件的物理模型和数学模型的分析,设计并完成了如图4所示的加料衬套的加工制造,其结构参数如表3所示。

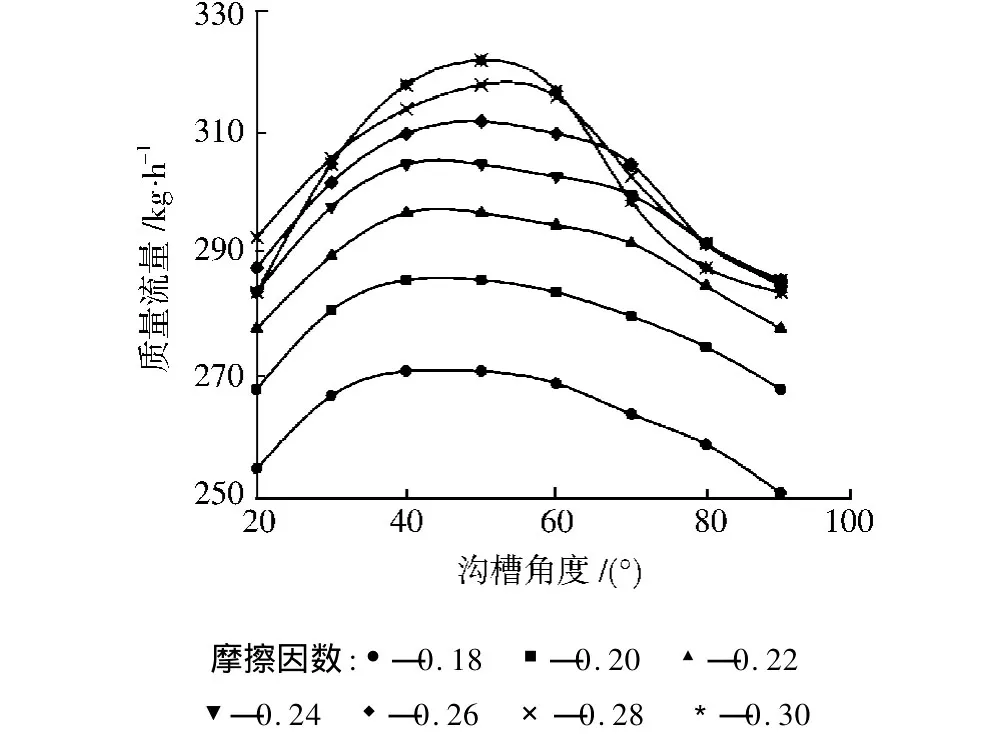
图3 质量流量与沟槽螺旋角的关系Fig.3 Effect of helical angle on the mass flow rate

图4 加料衬套示意图Fig.4 Diagram of feeding sleeve

表3 加料衬套的几何结构参数Tab.3 Geometric parameters of feeding_sleeve

2.1 固体输送段压力分布曲线

初始压力 Po=0,螺杆转速n=40 r/m in,修正系数r=3000。将沟槽、螺杆几何参数及加工工艺参数代入式(5),得到沿螺杆螺槽方向固体输送段压力分布曲线,如图5所示。图5为充分考虑了固体塞的可压缩性及其加速度的情形下沿螺杆螺槽方向固体输送段压力分布曲线图。曲线变化趋势表明:在固体输送段沿螺杆螺槽方向压力值迅速增加,正位移输送机理下不同的机筒和螺杆表面摩擦因数对固体输送段的建压能力有很大的影响,较小的摩擦因数下固体输送段末端处压力峰值可达到22 M Pa左右,这一数值远远高于同级别几何结构参数的光滑机筒挤出机,因此在压缩段、计量段形成的正压力流在提高产量的同时也确保了挤出制品时的良好稳定性。曲线起点处压力值为0,说明挤出机在饥饿喂料状态下仍可稳定建压,这与实际中情形是相符的,从而弥补了Darnell-Mol理论初始压力必须不为0的缺陷。

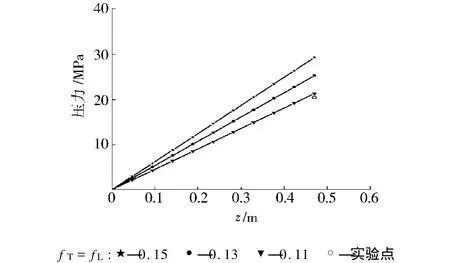
图5 不同摩擦因数下固体输送段压力分布曲线Fig.5 Curve fo r pressure distribution in solid conveying zone under different coefficient of f riction

Franzkoch[10]得到的基于摩擦拖曳输送机理下直槽IKV挤出机和光滑机筒挤出机压力分布曲线如图6所示,其中螺杆直径为45 mm,转速为66 r/min。对比图5和图6可以发现,在相同的螺杆直径、相近的螺杆转速下,螺旋沟槽挤出机与直槽 IKV挤出机在固体输送段末端产生的压力值相近,均远高于光滑机筒挤出机在固体输送段末端产生的压力值。它们具有相似的压力分布曲线,都为类似于直线式的建压机理,可以迅速在固体输送段末端产生沿螺杆轴向上的压力峰值,从而实现产量独立于背压的稳定挤出。但在本文中使用的螺旋沟槽挤出机是基于文献[6]中正位移输送理论指导下设计的,是基于正移位输送机理完成固体输送的,因此,固体塞在输送过程中受到的一切摩擦力均为阻力,这在本质上不同于基于摩擦拖曳输送机理下设计的直槽IKV挤出机,由此可在保证固体输送段建压能力的前提下,适当减小固体输送段机筒及螺杆表面摩擦因数以实现低比能耗下的稳定挤出,这也是在根本上优于传统直槽IKV挤出机的原因。

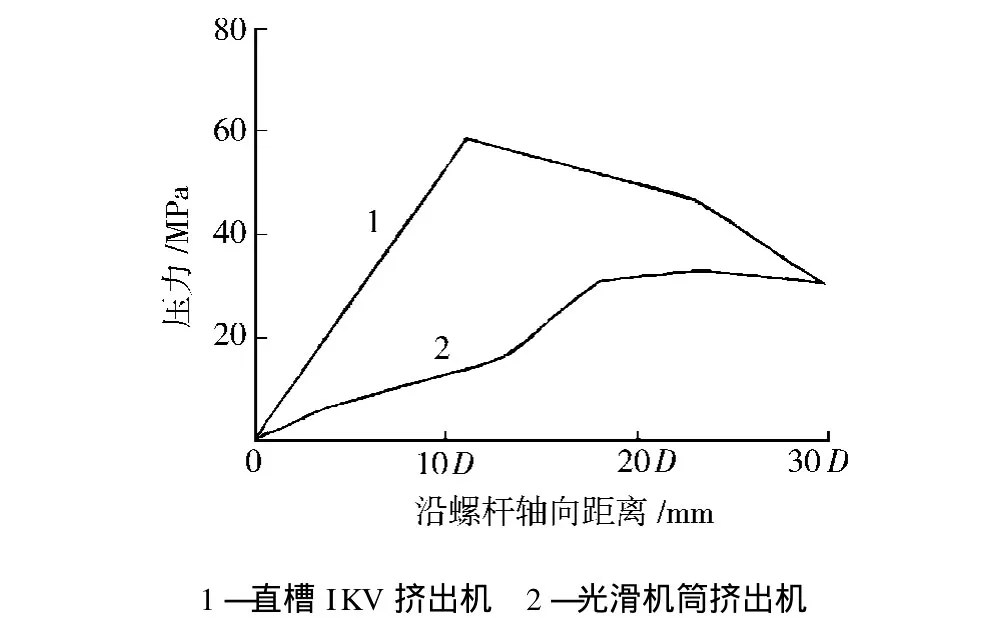
图6 直槽IKV挤出机和光滑机筒挤出机的压力分布曲线Fig.6 Curves for pressure distribution of IKV extruder and conventional extruder with a smoo th feed section

2.2 螺杆转速对固体输送段末端压力影响

图7反映了正位移输送机理下螺杆转速与固体输送段末端压力峰值之间的关系。从图7可以看出,随着螺杆转速的增加,理论计算与实验测量得到的固体输送段末端压力峰值变化趋势相同,均略有增大。这是由于螺杆转速增加时固体输送率增大造成的。同时由于固体塞始终在螺杆螺棱推进面和加料套螺棱推进面的共同推力作用下整体向前稳定输送,避免了物料漏流、固体塞打滑及物料间内摩擦的出现,因此固体输送段末端压力峰值只有小幅的波动,从而有效保证了物料的稳定挤出。

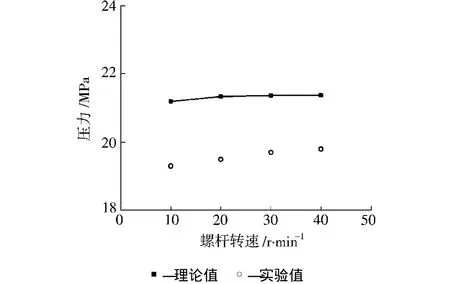
图7 螺杆转速对固体输送段末端压力的影响Fig.7 Effect of screw rotating speed on limit pressure at the end of solid conveying section

3 结论

(1)螺旋沟槽单螺杆挤出机在初始压力为0时,亦可沿螺杆螺槽方向建立压力;

(2)螺旋沟槽单螺杆挤出机与直槽IKV挤出机具有相近的类直线式压力分布曲线,均在固体输送段末端达到沿螺杆轴向的压力峰值,实现产量独立于背压的稳定挤出;

(3)机筒及螺杆表面摩擦因数对螺旋沟槽单螺杆挤出机固体输送段末端压力峰值影响显著,摩擦因数略有增大,建压能力显著增强;

(4)螺杆转速对螺旋沟槽单螺杆挤出机固体输送段末端压力峰值影响较小;

(5)固体输送段建压方程式及固体塞速度方程式的求解及建压机理分析为螺旋沟槽单螺杆挤出机固体输送理论的进一步研究奠定了理论基础。

[1] 朱复华.挤出理论及应用[M].北京:中国轻工业出版社,2001:52-56.

[2] 伊藤公正,罗世华.用开槽进料段提高单螺杆挤出机的性能(连载之一)[J].塑料加工应用,1990,(4):42-56.

[3] 伊藤公正,罗世华.用开槽进料段提高单螺杆挤出机的性能(连载之二)[J].塑料加工应用,1990,(4):65-80.

[4] Potente H,Stenzel H,Bergedieck J.Output Computation in the Grooved-barrel Extruder with Regard to Various Conveyance Techniques[J].Advances in Polymer Technology,1990,10(4):285-295.

[5] Davis B A.Grooved Feed Single Screw Extruders-Improving Productivity and Reducing Viscous Heating Effects[J].Polymer Engineering and Science,1998,38(7):1199-1204.

[6] 潘 龙,贾明印,薛 平,等.螺旋沟槽单螺杆挤出机双螺棱推动理论模型的研究[J].中国塑料,2010,24(11):94-99.

[7] Kramer A.Experimence in Using Extruderswith Grooved Feed Zones[J].Kunststoffe,1988,78(1):21-26.

[8] Potente H.Methods of Calculating Grooved Extruder Feed Sections[J].Kunststoffe,1985,75(7):439-441.

[9] M iethlinger J.Modelling the Solids Feed Section in Grooved-feed Extruders[J].Kunststoffe,2003,93(4):49-53.

[10] Franzkoch B,Menges G.Grooved Forced-feeding Zones Can Improve Extruder Performance[J].Plastics Engineering,1978,(7):51-54.

Pressure Distribution in Solid Section of Helically Grooved Feed Single-screw Extruders

PAN Long,JIA Mingyin,XUE Ping＊,JIN Zhiming,TANG Guangli
(College of Mechanical and Electrical Engineering,Beijing University of Chemical Technology,Beijing 100029,China)

In the feeding sleeve several helical grooves were opened up.Regarding the materials between groove and channel as a so lid-p lug,the barrel and screw could be considered as an indivisible system to cooperatively push forward the materials in solid conveying zone.A mathematical model was formulated to consider the influences of the compressibility and the acceleration of the materials,the pressure and the velocity of the solid-p lug in the down-channel were calculated.Finally,it was found that when the solid-plug was being carried by way of positive conveying,the peak pressure at the end of solid conveying zone was strikingly promoted and the materials could be stably extruded.

single-screw extruder;solid conveying;helical groove;pressure distribution;double flight driving

TQ320.66+3

B

1001-9278(2011)04-0102-05

2010-07-10

国家自然科学基金资助项目(50873014)

＊联系人,xuepmail@263.net