PCA分块Rees矩阵半群

2011-11-27李勇华

华南师范大学学报（自然科学版） 2011年1期

关键词：本原同构分块

陈晔,李勇华

(华南师范大学数学科学学院,广东广州 510631)

格林关系是研究正则半群的一个重要工具,推广正则半群的一个有效途径是建立新的格林关系来研究更大的半群类.MCALISTER[1]和PASTIJN[2]首先提出格林*-关系,其定义如下:设S是半群,则

H*=L*∩R*,D*=L*VR*.

若半群S的每个L*-类和每个R*-类都含有一个幂等元,则称S为富足半群.

文献[3]利用S-系的张量积[4]阐述了PA分块Rees矩阵半群的概念,下面引入一些准备知识.设I,Λ≠,Γ(≠)对I和Λ分别进行分划得到:P(I)={Iγ:γΓ},P(Λ)={Λγ:γΓ}.约定用i,j,k,h表示I中的元;用λ,μ,ν,ρ表示Λ中的元;用α,β,γ,δ表示Γ中的元.对于任意的序对(α,β)Γ×Γ,设Mαβ是这样一个集合,它满足:对于任意的α,Mαα=Tα是仅含一个幂等元eα的幺半群且对于α≠β,要么Mαβ=,要么Mαβ是一个(Tα,Tβ)-双系.0(零元)表示不在任何Mαβ中的元.

文献[5]定义了半群上的格林∘-关系,从而获得了一类半群——∘-富足半群:设S是半群,则

H°=L°∩R°,D°=L°∨R°.

如果半群S的每个L°-类和每个R°-类都含有幂等元,则称S是∘-富足半群.不难验证L°是S上的等价关系.设S是半群,则L⊆L*⊆L°.若S是正则的,则L=L*=L°.

本文第1节给出了格林∘-关系的几个基本性质.第2节用∘-幺半群和这类半群的双系构造了一类新的半群——PCA分块Rees矩阵半群.FOUNTAIN[3]用可消幺半群和双系构造了PA分块Rees矩阵半群,并证明了每一个含零的本原富足半群都同构于一个PA分块Rees矩阵半群.作为半群类的扩张，本文第3节证明了每一个含零的本原∘-富足半群都同构于一个PCA分块Rees矩阵半群.最后给出例子说明一个半群可以是本原∘-富足半群,但不是本原富足半群.

对于本文中没有给出的术语和记号,请参阅文献[3]和文献[4].

1 ∘-关系的几个基本性质

命题2 设半群S满足条件(C),D°是S的一个D°-类且e是D°中一个幂等元.令A=B∩C,其中B=∪{L°f:f2=f且fDe},C=U{R°g:g2=g且ggDe}.则

(4)含幂等元的集合A中任意2个H°-类都是互相同构的∘-幺半群.

从而H°f和H°g是互相同构的∘-幺半群.

引理1 设e,f是半群S中的幂等元.若H°=R°e∩L°f≠,则S中的乘法使得H°成为一个(H°e,H°f)-双系.

证明略.

2 PCA分块Rees矩阵半群

首先给出关于PCA分块Rees矩阵半群的定义:分块Rees矩阵半群M°(Mαβ;I,Λ,Γ;P)若满足下面3个条件,则称之为PCA分块Rees矩阵半群:

事实上,条件(C)°使得每一个Tα成为一个∘-幺半群.

命题4 设S=M°(Mαβ;I,Λ,Γ;P)是一个PCA分块Rees矩阵半群,则:

(2)(a)iλ,(b)jμ为S中非零元,(a)iλL°(b)jμ当且仅当i=j;

(3)(a)iλ,(b)jμ为S中非零元,(a)iλR°(b)jμ当且仅当λ=μ;

(4)S是∘-富足的,且S中所有非零幂等元都是本原的;

2.3 两组患者手术中、手术后并发症比较观察组和对照组手术均顺利完成，手术中及手术后无并发症发生，均无中转开腹，两组手术中、手术后并发症差异无统计学意义（P＞0.05）。

(3)证明过程类似于(2).

(a)iλ∘(b)jμ∘(a)iλ=(apλjbpμ ia)iλ=(a)iλ,
(b)jμ∘(a)iλ∘(b)jμ=(bpμ iapλjb)jμ=(b)jμ,

引理2 定义映射ψE,E,ηE如下:

则ψE,E,ηE都是双射并且满足iIα(λΛα)当且仅当iψE⊆αηE(λE⊆αηE).

定理1 设S=M°(Mαβ;I,Λ,Γ;P),T=M°(Nγδ;J,Ω,Δ;Q)是PCA分块Rees矩阵半群.则S和T是同构的当且仅当下面几个条件成立:

(1)存在ψ:I→J,:Λ→Ω,η:Γ→Δ使得iIα(λΛα)当且仅当iψJαη(λΩαη);

(abc)φαβ=(aφαγ)(bφγδ)(cφδβ);

证明设θ:S→T是一个同构映射.

(2)由引理3知Mαβ=当且仅当H°i(α)λ(β)=.对于任意的αΓ，选取(i(α),λ(α))Iα×Λα,使得pλ(α)i(α)是Tα中的一个单位.由于是S中的幂等元,则它在θ下的象是T中的幂等元.令j(αη)=i(α)ψ,μ(αη)=λ(α),则qj(αη)μ(αη)是Uαη中的单位.则由引理3,对于任意满足Mαβ≠的(α,β)Γ×Γ,有映射ψαβ:Mαβ→H°i(α)λ(β)和ψαη,βη:Nαη,βη→H°j(αη)μ(βη).设θαβ:H°i(α)λ(β)→H°j(αη)μ(βη)是θ在H°i(α)λ(β)上的限制.则显然θαβ是双射且可以记则对于任意的aMαγ,bMγδ,cMδβ(其中Mαγ,Mγδ,Mδβ都是非空的),有

(aφαγ)(bφγδ)(cφδβ).

(pλi)i(β)λ(α)=(eβpλieα)i(β)λ(α)=(eβ)i(β),λ∘(eα)i,λ(α),

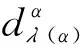
由定理1的(2)知φαα是Tα到Uαη=Nαη,αη上的同构.若对于任意的α,Tα和Uαη在同构意义下相等,从而φαβ是Mαβ到Nαη,βη上的(Tα,Tβ)-同构.

3 本原∘-富足半群

如果半群中每个非零幂等元都是本原的,那么称这个半群是本原半群.这一节主要阐述这样一个结论:每个含零的本原∘-富足半群都同构于一个PCA分块Rees矩阵半群.下面是与文献[3]中结论平行的几个结论(证明略).

引理4 若e,f是含零的本原半群S中的幂等元且eS⊆fS(Se⊆Sf),则eS=fS(Se=Sf)或者e=0.

假设S是含零的本原∘-富足半群.设a,b是S中的非零元,e,f是S中的幂等元且aR°e,bL°f.另外考虑条件(Z):ba=0当且仅当fe=0.

推论2 在一个含零的本原∘-富足半群S上,

(1)H°关系是同余关系;

(2)若H°是S的一个H°-类,则H°是S的子半群,或H°H°={0}.

命题5 设e,f含零的本原∘-富足半群S中的幂等元.若e,f不是D-相关的且ef,fe都是非零元,则H°ef且H°fe都是S的子半群,其中不含恒等元.

证明略.

定理2 若S是含零的本原∘-富足半群,则S同构于一个PCA分块Rees矩阵半群;且任意PCA分块Rees矩阵半群都是含零的本原∘-富足半群.

证明由命题4的(4)知PCA分块Rees矩阵半群是含零的本原∘-富足半群.

定理2表明当S是正则半群时,利用命题4可得这一矩阵半群的其他性质.设M°=M°(Mαβ;I,Λ,Γ;P)是正则PCA分块Rees矩阵半群.由命题4的(6)知,零元(a)iλ满足a是Tα中的单位.故只要α≠β,则Mαβ是空集,且每个Tα是群.反之,M°满足这些条件,则由命题4知M°是正则的.在这种情况下M°同构于Rees矩阵半群