ZOOM-FFT在检测轨道电路移频信号参数研究中的误区
2011-11-26熊信民
王 安,熊信民
(西北工业大学 自动化学院,西安 710129)
铁路在国民经济的发展中起了很重要的作用。为了保证行车安全,需要定期检测轨道电路的相关运行参数,而现行的轨道电路主要采用移频信号作为控制信息,因此及时了解轨道电路移频信号的状态,能够为线路检修工作提供极大的方便。
目前,很多对移频信号参数的检测方法的研究[1~3],都采用ZOOM-FFT进行频谱细化,期望达到高频率分辨率。而在实际工程条件下,该方法并不能真的提高频率分辨率,只是降低了计算的复杂程度。通过MATLAB仿真实验,验证了用ZOOM-FFT方法并不能任意提高频率分辨率,该方法要受到采样时间长短的限制。
1 轨道电路移频信号分析
我国轨道电路的制式主要是移频轨道电路,包括国产18信息移频轨道电路和引进法国UM71型并加以国产化的ZPW-2000型移频轨道电路。二者均以频率作为参数,采用频率调制的方法,把低频信息搬到较高的载频上,以形成振幅不变、频率随低频信号的幅度做周期性变化的调频信号,实现信息的传递。
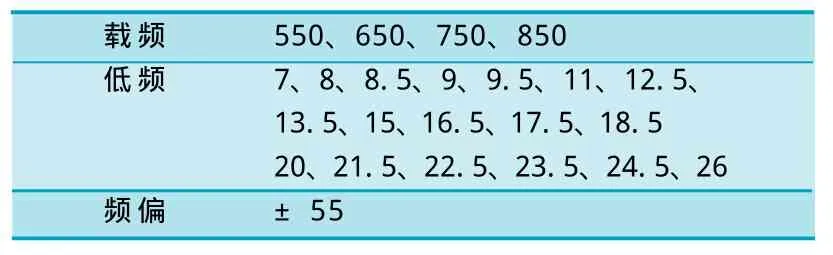
表1 国产18信息移频轨道电路的移频信号

表2 ZPW-2000型移频轨道电路的移频信号
这样就产生了2种制式的移频信号,其参数载频、低频和频偏的频率如表1和表2所示。(单位:Hz)。
移频信号的时域表达式[4]为:
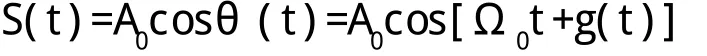
其中g(t)=∫kf(t),A0为移频信号的振幅,θ(t)为移频信号的瞬时相位,Ω0为载频的角频率,f(t)表示低频调制方波信号,k为系数,代表移频器的灵敏度,单位是Hz/V。
将上式用傅里叶级数展开,经过变换可得移频信号的频谱表达式[4]如下:
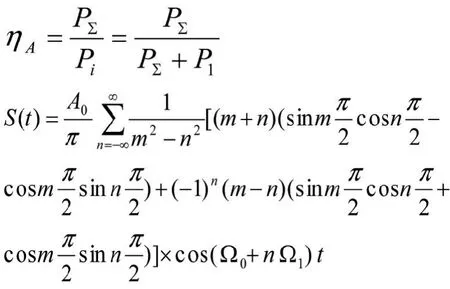
式中,Ω1为基频,m为移频指数,n为边频数,n=…-2,-1,0,1,2…。
移频信号的理论频谱如图1和图2。

图1 国产18信息移频信号理论频谱

图2 ZPW-2000型移频信号理论频频
通过分析移频信号的理论频谱的特点可知:对于国产18信息轨道电路,将峰值最大的两个边频对应的频率相加求取平均值可以得到信号的载频频率,两条相邻边频对应频率之差的绝对值为信号的低频调制频率;对于ZPW-2000型轨道电路,峰值处的对应频率即为信号的载频频率,两条相邻边频对应频率之差的绝对值为信号的低频调制频率。
2 问题的提出
反映移频信号的参数有载频和低频调制频率。现场对以上参数进行检测,与预先设定的标准值进行比较,从而判断发送移频信号的设备是否工作正常。
检测参数达到的技术指标如下:
(1)载频:分辩率为0.1 Hz ,误差为0.2 Hz±1 个分辩率。
(2)低频:分辩率为0.01 Hz,误差为0.03 Hz±1 个分辩率。
对移频信号做频谱分析时,频率分辨率df=fs/N,其中fs为采样频率,N为采样点数。提高频率分辨率的2种途径:增加采样点数N、降低采样频率fs。但是增加采样点数的方法需要处理大量的数据,而且需要大量的存储空间,对硬件要求很高;而降低采样频率的方法会使信号的频谱产生混叠,不能保证频率的检测精度。采样时间(即使用的信号的长度)T=N/fs,因此频率分辨率反比于采样时间,提高频率分辨率就意味着采样时间会增加,不能满足测试仪表的实时性要求。这就需要找到一种方法在提高频率分辨率和降低采样时间之间做一个平衡。
3 ZOOM-FFT方法实质
研究发现,ZOOM-FFT频谱细化分析能提高局部谱线的分辨率是相对而言的。
例如:采样频率为fs,做N点的ZOOM-FFT频谱细化,如果细化倍数为D,频率分辨率为△f1=fs/(D*N);直接做N点的FFT变换,频率分辨率为△f2=fs/N,这样△f1/△f2=1/D,相当于做N点ZOOM-FFT频谱细化比做N点FFT变换频率分辨率提高了D倍。注意到要做N点ZOOMFFT实际中需要采样D*N个点,实际上频率分辨率已经达到△f1=fs/(D*N),只是没有做D*N点的FFT变换而已。因此,ZOOM-FFT并没有提高频率分辨率,只是降低了计算的复杂程度。
4 计算机仿真验证
这里选用3个频率相近的正弦波叠加组成的周期信号,分别采用ZOOM-FFT频谱细化和普通FFT处理,以下3组MATLAB仿真结果可以验证我们对ZOOM-FFT的看法。
(1)第1组仿真参数设置及分析
3个正弦波频率分别为:f1=7 Hz,f2=7.2 Hz,f3=8 Hz。采样频率fS=200 Hz,采样点数N=1024,细化倍数D=10,普通FFT长度为nfft=512。
计算可知,以200 Hz的频率采样1024点,ZOOM-FFT频率分辨率实际上可以达到△f=fs/N=200/1024=0.195,具备将f1和f2分开的能力。而作nfft=512点普通FFT变换频率分辨率为△f2=fs/nfft=200/512=0.391,显然不能分辨f1和f2。MATLAB仿真结果如图3。

图3 ZOOM-FFT与普通FFT仿真结果1
理论上信号的频谱有3个峰值,在图3中,普通FFT仿真后丢失了一个峰值,得到的2个峰值频率分别为7.031 Hz和8.203 Hz,ZOOM-FFT仿真后的3个峰值频率分别为6.977 Hz、7.211 Hz和8.031 Hz。对比仿真结果可知普通FFT不能分辨f1和f2,而ZOOM-FFT能分辨f1和f2,与计算预想的结果相同。
(2)第2组仿真参数设置及分析
3个正弦波频率分别为:f1=7 Hz,f2=7.1 Hz,f3=8 Hz。采样频率fS=200 Hz,采样点数N=1024,细化倍数D=10,普通FFT长度为nfft=512。
计算可知,以200 Hz的频率采样1024点,ZOOM-FFT频率分辨率实际上可以达到△f=fs/N=200/1024=0.195,不具备将f1和f2分开的能力。而作nfft=512点普通FFT变换频率分辨率为△f2=fs/nfft=200/512=0.391,显然也不能分辨f1和f2。MATLAB仿真结果如图4。
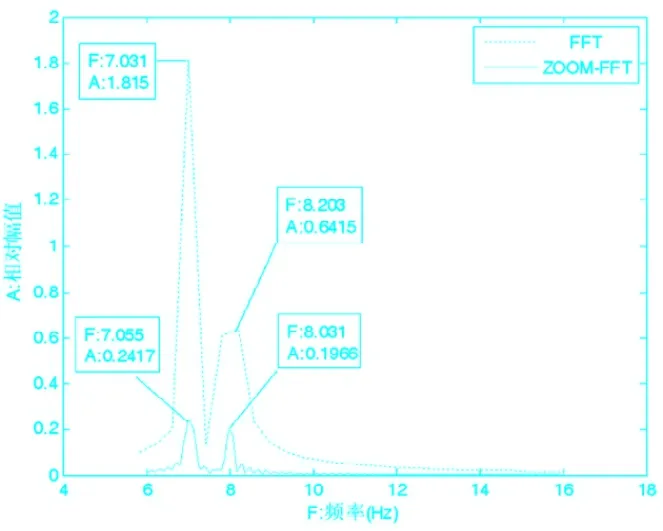
图4 ZOOM-FFT与普通FFT仿真结果2
理论上信号的频谱有3个峰值,在图4中,普通FFT仿真后丢失了一个峰值,得到的2个峰值频率分别为7.031 Hz和8.203 Hz,ZOOM-FFT仿真后也丢失了一个峰值,得到的2个峰值频率分别为7.055 Hz和8.031 Hz。对比仿真结果可知普通FFT不能分辨f1和f2,而ZOOM-FFT也不能分辨f1和f2,与计算预想的结果相同。
(3)第3组仿真参数设置及分析
3个正弦波频率分别为:f1=7 Hz,f2=7.1 Hz,f3=8 Hz。采样频率fS=100 Hz,采样点数N=1024,细化倍数D=10,普通FFT长度为nfft=512。
计算可知,以100 Hz的频率采样1024点,ZOOM-FFT频率分辨率实际上可以达到△f=fs/N=100/1024=0.098,具备将f1和f2分开的能力。而作nfft=512点普通FFT变换频率分辨率为△f2=fs/nfft=200/512=0.391,显然不能分辨f1和f2。MATLAB仿真结果如图5。

图5 ZOOM-FFT与普通FFT仿真结果3
理论上信号的频谱有3个峰值,在图5中,普通FFT仿真后丢失了一个峰值,得到的2个峰值频率分别为7.031 Hz和8.008 Hz,ZOOM-FFT仿真后的3个峰值频率分别为6.977 Hz、7.113 Hz和8.012 。对比仿真结果可知普通FFT不能分辨f1和f2,而ZOOM-FFT能分辨f1和f2,与计算预想的结果相同。
分析以上3组仿真结果可知,ZOOM-FFT的频率分辨率与实际的采样频率和采样点数有关系,要达到与普通FFT相同的频率分辨率,需要采样更多的点数,这样采样持续时间很长。ZOOMFFT只是在计算中处理少量的点数,降低了计算的复杂程度。而在工程应用中,现场测试设备对实时性有较高要求,不能允许测试时间过长。如对ZPW-2000型轨道电路移频信号载频f0=2000 Hz,低频f1=10.3 Hz来说,要求载频分辨率为0.1 Hz,ZOOM-FFT方法实际采样时间需要10 s,使用该方法也达不到实时性的要求。
5 结束语
本文在分析轨道电路移频信号的频谱特点的基础上,研究发现ZOOM-FFT方法达不到工程中现场测试设备对实时性的要求,指出该方法在研究检测轨道电路移频信号参数中的误区。对研究移频信号的检测方法有一定的指导意义,避免在设计移频信号参数测试仪时做重复的研究。同时也表明了理论研究和工程应用存在差距,在做工程产品开发时要分析实际需求,多考虑限制条件,而不是只做理论上的分析。
[1]武中奇,杨世武. ZFFT算法在铁路移频信号分析中的应用及其DSP实现[J]. 铁道通信信号,2008,44(7):32-34.
[2]吕剑飞,卢 迪. ZOOMFFT算法在车载FSK信号高精度检测中的应用[J]. 自动化技术与应用,2007,26(1):63-64.
[3]焦玮琦,陈特放. 基于局部频谱细化的轨道移频信号高精度检测[J]. 机车电传动,2009(2):48-50.
[4]杨少军,李杭生. 基于DSP的移频机车信号分析研究与实现[D]. 武汉大学硕士学位论文,2005(4):8-10.
