单向阀内部振动的分析

李 阳

(北京工商大学理学院，北京100048)

时，单向阀运动过程稳定.

单向阀内部振动的分析

李 阳

(北京工商大学理学院，北京100048)

在双组元推进系统中，使用单向阀控制气体介质单向流动.当上游气源接通时，单向阀受到瞬间冲击激励，其阀芯与弹簧构成简单的弹簧质量系统，在阻尼作用下，与非线性阀座或刚性阀座碰撞，会出现复杂的共振现象，导致整个气压系统不稳定.文中建立了单向阀弹簧质量系统的数学模型，并分析了所产生的共振现象，为单向阀设计、试验和使用中控制共振现象提供了一种方法.

双组元推进;单向阀;共振

单向阀是一种只允许流体沿着一个方向流动的阀门［1］.当单向阀上游压力高于下游压力一定值时阀门开启，接通气体增压管路;当下游压力高于上游压力一定值时，阀门关闭，切断气体增压管路.在双组元推进系统中，使用单向阀控制气体介质单向流动.但在应用过程中，当上游气源瞬间打开时，单向阀受到瞬间冲击激励会产生振动，单向阀的阀芯与弹簧构成的简单弹簧质量系统，在阻尼作用下，与具有非线性的阀座或刚性的阀座碰撞，会产生复杂的共振现象，若共振不能短时间衰减将导致整个气压系统不稳定.单向阀在外加气源激励下周期振动的现象，随着激励源不同，振动频率的高低也不同，振动频率范围比较宽.因此，根据单向阀结构进行数学建模，从理论角度分析，可以帮助设计人员定性和定量相结合分析单向阀振动现象，提出有效抑制单向阀的瞬态振动的改进设计的措施.文献［2-3］中采用仿真分析对某种特殊结构单向阀的充气振动和活门充气振动开展了研究，文献［4-6］对液体介质止回阀的工作原理和启闭动态特性进行了研究.本文对气体介质单向阀，根据单向阀实际结构提出了分析模型，利用非线性弹簧质量系统有关理论建立数学模型，对单向阀充气共振现象进行了分析，根据分析结果可以指导修改参数，达到抑制或消除气体介质单向阀共振现象的目的.

1 建模

单向阀的核心结构是弹簧、动阀芯和密封口，当入口气压增大后，气源压力克服弹簧力将阀芯打开，当下游压力和弹簧力大于上游压力后，推动阀芯使单向阀关闭.因此，单向阀的实物原理图近似可以用图1表示.该原理图假定弹簧一端固定，另一端与阀芯接触，阀座一侧固定，另一端与阀芯接触.根据原理图，定义相关变量并绘制几何模型，如图2所示，将弹簧用质量M、刚度K表示，粘性当量阻尼系数用re表示，将塑料阀座部分模拟成非线性弹簧(用Kz表示非线性刚度)，而将阀芯模拟为质量m的刚性质量块，弹簧受进口压力为P，质量块的位置用变量x表示，质量块的位移用变量u表示，质量块与阀座接触时的位置为x=L.

2 分析

根据单向阀原理图，单向阀处于密封状态时，阀芯被弹簧压死在阀座上.当上游气源阀门打开后，一个由气源产生的力施加到质量块上，推动单向阀打开，为了分析的方便，假设一种理想的情况，气源压差产生的力和弹簧力平衡使阀芯处于动态平衡状态，当气源关闭后，弹簧质量系开始运动，当质量块运动到x=L时，运动质量块受到非线性弹簧的作用力，质量块被非线性弹簧弹回，当质量块与阀座(即非线性弹簧)脱离后，弹簧质量系开始自由振动.

图1 单向阀原理图

图2 单向阀几何模型

首先，分析质量块在进口压力作用下与阀座(即非线性弹簧)脱离后的运动情况.此时，弹簧质量系可以按照简单的线性弹簧质量系统的自由振动进行分析.可以不考虑弹簧的分布质量，将弹簧看作无质量元件，作阻尼自由运动.质量块的运动可以用阻尼自由运动方程式表示［7］:

对式(1)两端除以m，得

式中，δ称为阻尼系数，当re=0时，可求得无阻尼系统的固有频率ω0，δ与ω0之比称为阻尼比，记作ζ，因此，

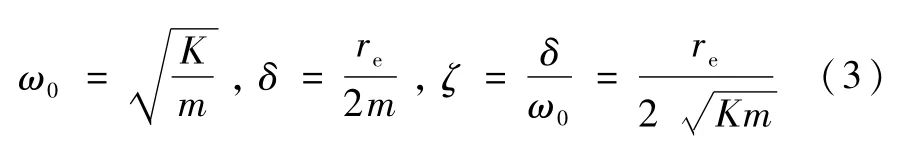
将式(3)代入式(2) 并求解得u的不同解:

因此，当阀芯与弹簧构成的弹簧质量系统与阀座未接触情况下，在气体或摩擦阻尼作用下运动，当ζ＞1，即也就是，当粘性当量阻尼系数

时，单向阀运动过程稳定.

其次，分析质量块与非线性弹簧接触后的运动情况.根据图2模型，弹簧运动可用表示为

根据单向阀的几何模型和运动过程分析，列出边界条件:

其中，非线性弹簧力表示为K1u+K2u2+K3u3.

因为瞬时变形u是x的函数，又是t的函数，令u=φ(x)ψ(t) ，则，式(5)表示为:

式(18)左右两端分别为对时间和位移的表达式，令左右两端等于某一常数 -ω2，则式(8)变为方程组:

方程组(9)解得:

re/ω=1为临界阻尼状态，re/ω＞1为过阻尼状态，re/ω＜1为欠阻尼状态，从而，单向阀振动时运动方程可以表示为u=φ(x)ψ(t)

根据边界条件式(6)，得c1=0，从而

由边界条件式(7)可以求解共振频率ω.

从式(12)可见，令阻尼固有角频率 ωd=系统的自由振动过程是一振幅随时间不断衰减的等频运动，且在粘性当量阻尼很小时，阻尼固有角频率ωd和无阻尼固有角频率ω十分接近.

进一步分析，阀座若用橡胶材料等软密封材料制作，阀座可以模拟为非线性弹簧，式(12)描述了这种情况.若采用硬塑料或金属等硬密封材料制作，则阀芯受到刚性反弹，外加激励可以模拟为脉冲冲击力.此时，单向阀振动时运动方程可通过式(5)(6)和式(13)联立求解.

单向阀振动时的运动方程可以启发我们，抑制单向阀共振问题可以在弹簧设计时调整粘性当量阻尼系数re，使re＞ω，则单向阀弹簧质量系统在外加激励后的运动是趋向稳定的.其中，根据弹簧设计理论［8］式中， c′为弹簧材料单位长度单位速度的阻尼力，ms为弹簧工作部分质量，L′为弹簧长度.对于re，虽然影响它的因素很多，一般只能靠实验来确定，但对于单向阀弹簧质量系统，可以通过调整弹簧工作部分质量ms和弹簧长度L′来调整re，工程上，阀芯质量m可以等效到ms中一并考虑，另外，还可以在气压供给系统中，在单向阀上游增加气容，缓冲外部激励对单向阀的瞬间冲击，使单向阀弹簧质量系统实现 re＞ω，从而使单向阀在外加激励作用下不发生共振.

3 结论

单向阀通过分布质量弹簧、密封阀芯和阀座模拟成弹簧质量系统.经分析，在外加气源激励关闭后，单向阀在阻尼比re/ω＜1时情况下发生共振，阻尼固有角频率，系统的自由振动过程是一振幅随时间不断衰减的等频运动.在粘性当量阻尼很小时，阻尼固有角频率ωd和无阻尼固有角频率ω十分接近.抑制单向阀共振问题可以在弹簧设计时调整粘性当量阻尼系数re，使re＞ω，则单向阀弹簧质量系统在外加激励后的运动是趋向稳定的.调整弹簧粘性当量阻尼系数re可以通过调整弹簧工作部分质量ms、阀芯质量m和弹簧长度L′来实现.另外，在单向阀上游增加气容可以缓冲外部激励对单向阀的瞬间冲击，将能抑制单向阀在气压系统中发生的共振问题，根据文［2-3］，还可以在管路中增加节流圈，通过调整节流圈的直径，达到抑制共振现象的目的.

［1］ 彭熙伟，陈建萍，李金仓.单向阀的特性及应用［J］.液压与气动，2004(1):60-61

［2］ 师好智，万曼影，徐洁晶.某特殊结构单向阀的充气振动研究［J］.机床与液压，2006(7):150-153

［3］ 师好智，万曼影，刘学军，等.单向活门充气振动的建模与仿真［J］.计算机仿真，2006，23(6):289-291

［4］ 樊淑趁，吴宣友.液控单向阀动态特性的分析及试验研究［J］.煤矿机械，1994(2):9-13

［5］ 雍歧卫，翟德刚.止回阀水力特性分析及水击计算［J］.阀门，2003(5):1-4

［6］ 韩旭，周羽.对冲式止回阀原理及启闭特性分析［J］.核动力工程，2006，27(1):66-69

［7］ (英)沃尔肖(Walshaw，Arthur Clifford)著，朱世杰，邱学章译校.机械振动与应用［M］.北京:中国铁道出版社，1994

［8］ 张英会，刘辉航，王德成.弹簧手册［M］.北京:机械工业出版社，1997

Analysis of Internal Resonance of Check Valve

LIYang
(College of Science，Beijing Technology and Business University， Beijing 100048， China)

In a bipropellant propulsion system，a check valve is used to control gas unidirectional flow.A impulsive force is applied on the check valve when upstream gas source is switched on piston and spring of the check valve constituting a simple mass-spring system with damp，in collision with nonlinear seat or rigid valve seat， internal resonance can occur， these resulting in whole pneumatic system instability.We give a mass-spring model of the check valve is given and the internal resonances is analyzed in the paper.This result can provide a method for controlling internal resonance of the check valve.

bipropellant propulsion system;check valve;resonance

V448

A

1674-1579(2011)02-0060-03

10.3969/j.issn.1674-1579.2011.02.011

2011-01-15

李 阳(1975-)，女，辽宁人，博士，讲师，研究方向为控制及应用(e-mail:lyanghit@yahoo.com.cn).