伽罗瓦域运算的软件实现

陈志江，董 文，贾中云

(杭州师范大学信息科学与工程学院，浙江 杭州 310036)

伽罗瓦域运算的软件实现

陈志江，董 文*，贾中云

(杭州师范大学信息科学与工程学院，浙江 杭州 310036)

有限域是编码理论中相当重要的代数基础知识，有限域上的运算也显得非常重要.文章通过研究有限域的特点之后，给出了典型有限域GF(2n或3n)(n∈N)上加法与乘法的计算机实现.仿真结果表明，典型有限域上的加法和乘法都得到了很好的实现，具有潜在的实用价值.

有限域；加法；乘法

0 引 言

有限域运算主要有加法、乘法、幂运算、二次方和模逆等，文章主要讨论两种最基本的域运算——加法和乘法，并且在软件上实现它.目前存在许多这两种运算的算法，从方便实现上来看，二进制域是GF(2n)最具有吸引力的，运算只涉及到移位和按位的模2加，这个在用软件实现上很有诱惑力.像Montgomery算法[1]、固定窗口算法[2]等都可以很好的实现域运算.

1 代数理论基础

1.1 域的概念

表1 常用本原多项式Tab.1 Common primitive polynomial

定义1 若S是一个非空集合，并且在S内的一种代数运算(用▽表示)满足以下要求：

a) 封闭性，∀α,β∈S，∃α▽β∈S；

b) 结合律，∀α,β∈S，∃(α▽β)▽γ=α▽(β▽γ)；

c) ∃恒等元ε∈S，∀α∈S，使得α▽ε=ε▽α=α；

d) ∀α∈S，∃α-1∈S，使α▽α-1=α-1▽α=ε.

这样就称这个集合S为一个群.如果∀α,β∈S，都有α▽β=β▽α，就称群S为阿贝尔群.

定义2 存在非空集合R，如果在R中定义了加和乘两种运算并且满足以下公理：

a)R关于加法构成阿贝尔群，加法恒等元记为0；

b)R中非零元素全体对乘法构成阿贝尔群，乘法恒等元记为1；

c) 加法和乘法满足分配律：α(β+γ) =αβ+αγ.

这样称R为域[3]，域中元素的个数就为域的阶.

1.2 本原多项式

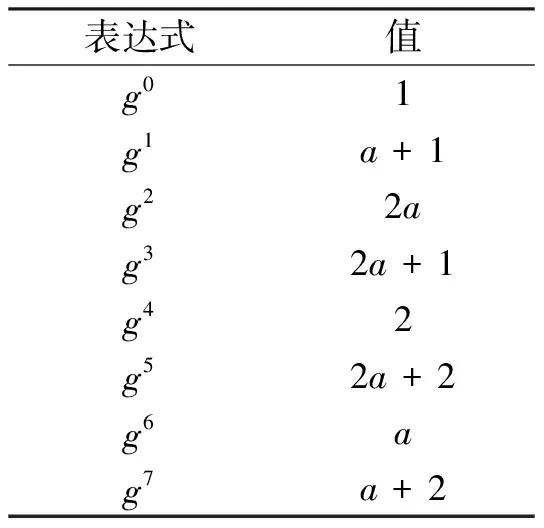
如果一个n次的不可约多项式f(x)能整除1 +zt而不能整除其它1 +zs，其中t= 2n- 1,s

2 伽罗瓦域

伽罗瓦域[5](或称有限域)的元素个数有限，GF(p)来表示p阶伽罗瓦域，每个伽罗瓦域GF(p)都至少包含了一个本原元素，它用来生成该域中的其它每个元素.把GF(p)延伸为一个含有pn个元素的域，称为GF(p)的扩展域，表示为GF(pn)，其中n是一个非零正整数.

举个例子，二进制域GF(2)就是GF(2n)其中的一个子域，除了0和1以外，在扩展域中还存在特殊元素，用新元素a来表示.在GF(2n)中任何非零元素都可以通过a的幂次来表示.因此，元素的无限集G就可以根据元素{0,1,a}形成，无限集G中后一个元素依次通过前面一个元素乘以a来得到：

G= {0,1,a,…,aj,…} = {0,a0,a1,…,aj,…} .

(1)

为了从G中得到有限元素的集合GF(2n)，所以G必须只能含有2n个元素，并且要对乘法封闭，故可以用以下不可约多项式来表示域元素对乘法的封闭：

a(2n-1)+1=0,

也就是：

a(2n-1)=1=a0.

(2)

有了这个限制条件，任何幂次等于或超过2n-1的域元素都可以降阶为幂次小于2n-1的元素：

a(2n+m)=a(2n-1)a(1+m)=a(1+m),

(3)

所以可以得到以下等价序列：

{0,1,a,a2,…,a(2n-2),a(2n-1),a2n,…}⟺{0,1,a,a2,…,a(2n-2),a0,a1,…},

(4)

从而就可以得到伽罗瓦域GF(2n)的元素由下面序列所构成：

GF(2n) = {0,1,a,a2,…,a(2n-2)}.

(5)

3 GF(p)的运算

如果有相同的生成元，素数域的加法是很简单的：

(x1a1+x2a2+ …+xrar) + (y1a1+y2a2+ … +yrar) = (x1+y1)a1+ … + (xr+yr)ar,

表2 GF(9)对数表Tab.2 The logarithms of GF(9)

换句话说就是把对应项的系数相加.

如果有相同的底，那么乘法也是简单的，可以看到gi·gj=gi+j，幂的次数都是经过模运算简化的.

为了更好进行这两种运算，需要建立一张对数表.因为gi=x的话，就称i为以g为底x的对数.

假设在GF(9)中，选择一个元素a，可以使a2= 2(超过这个整数对3取模)，从而得到g=1 +a是本原元，这样就可以得到如下对数表2.

这样就可以对照如上对数表简单计算乘法：(a+2)(2a+2)=g5*g7=g12=g4= 2.

4 GF(2n或3n)的运算[6]

在GF(2n)中，2n个元素的任意一个都可以由阶数小于或等于n- 1的不同多项式来表示，最高幂指数就是多项式的阶数.GF(2n)中的每个非零元素都可以用多项式ai(x)来表示，系数至少有一个不为零.对于i= 0,1,2,…,2n- 2，有

ai(x) =ai,0+ai,1x+ai,2x2+ … +ai,m - 1xm - 1,

(6)

这样两个元素的加法就为两个多项式中同幂次项系数进行模运算相加，即

ai+aj= (ai ,0+aj ,0) + (ai ,1+aj ,1)x+ … + (ai ,m-1+aj ,m-1)xm-1.

(7)

乘法就是把两个元素表示成指数形式，可以将指数直接相加取模，即

ai*aj=a(i + j)mod(2n-1).

(8)

5 实验结果

文章使用Matlab实现伽罗瓦域内的算法实现.

GF(2)内加法，仿真结果如表3.

表3 GF(2)内加法 Tab.3 Addition in GF(2)

GF(3)内加法，仿真结果如表4.

表4GF(3)内加法
Tab.4AdditioninGF(3)

a+b1+1=21+2=01+3=11+4=21+5=02+1=02+2=12+3=22+4=02+5=13+1=13+2=23+3=03+4=13+5=24+1=24+2=04+3=14+4=24+5=0

GF(4)内加法，仿真结果如表5.

表5 GF(4)内加法Tab.5 Addition in GF(4)

GF(3)内乘法，仿真结果如表6.

表6 GF(3)内乘法Tab.6 Multiplication in GF(3)

6 结 论

文章在充分分析伽罗瓦域特点的基础上，实现了伽罗瓦域上简单加法与乘法，算法简单明了.仿真结果表明，加法与乘法能够在伽罗瓦域上得到很好的实现.

[1] Fournaris A P,Koufopavlou O.Versatile multiplier architectures in GF(2k) fields using the Montgomery multiplication algorithm[J].Integration,2008,41(3):371-384.

[2] Lopez J,Dahab R.High-speed software multiplication in F2m[C]//Progress in Cryptology—indocrypt 2000.India Calcutta:Lecture Notes in Computer Science,2000:93-102.

[3] Lidl R,Niederreiter H.Introduction to Finite Fields and Their Applications[M].2th ed.Cambridge:Cambridge University Press,1994:1-332.

[4] 郭鑫,陈克非.求解本原多项式的快速算法[J].计算机工程,2008,34(15):146-147.

[5] Lidl R,Niederreiter H.Finite Fields[M].2th ed.Cambridge:Cambridge University Press,1997:1-124.

[6] 叶清贵.RS编译码的FPGA实现研究[D].上海:华东师范大学信息学院电子系,2006.

SoftwareImplementationinGaloisFieldOperation

CHEN Zhi-jiang,DONG Wen,JIA Zhong-yun

(College of Information Science and Engineering,Hangzhou Normal University,Hangzhou 310036,China)

Finite field is the considerable important basic knowledge of algebra in coding theory,so that the operation of finite field is obviously crucial.Through the researches on the characteristics of the finite field,this paper discussed the computer implementation of the addition and multiplication in a typical finite field GF (2nand 3n) (n∈N).The simulation results indicate that the addition and multiplication in typical finite field have been well implemented and have potential practical value.

finite field; addition; multiplication

2010-03-06

浙江省教育厅科研基金项目(Y200908330).

陈志江(1986—)，男，浙江绍兴人,计算机应用技术专业硕士研究生，主要从事无线多煤体传感器网络研究.

*通信作者：董 文(1969—)，男，内蒙古赤峰人，副教授，博士，主要从事无线传感网络研究.E-mail:dongwen69@163.com

10.3969/j.issn.1674-232X.2011.05.015

TP301.6

A

1674-232X(2011)05-0466-04