决定一个Dirac方程特征值集的整函数的讨论

梁银双，文生兰

(1.中州大学 信息工程学院，河南 郑州 450044；2.解放军信息工程大学 理学院，河南 郑州 450001)

微分算子的特征值的迹恒等式深刻揭示了微分算子的谱结构，在特征值的计算及其反问题以及孤子理论和可积系统理论中都有很重要的作用．关于Dirac方程的研究始于1921年， Hurwitz得到了Dirac方程的特征值、特征函数的渐近式[1]，并证明了在有限区间上Dirac系统的特征函数的完备性．Levitan和Sargsjan在文献[2-3]中对Dirac算子进行了系统的论述，包括常型、奇型以及周期情况的研究．虽然关于微分算子迹的研究已积累了大量文献，但是大多结果都是对局部方程局部边界条件而得到的．1981年，李梦如用文献[4]的方法，在文献[5]中得到了带有非局部边界条件的S-L算子的迹公式．关于带有非局部边界条件Dirac算子的迹公式的讨论，文献[6]中已讨论了一种情况．本文主要初步研究下述问题决定特征值的整函数：

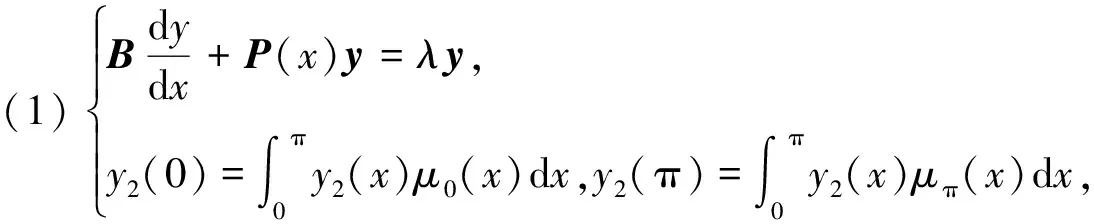
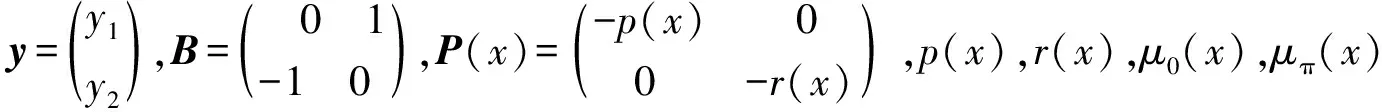
1 问题(1)的两个初值问题解的渐近估计

为了给出问题(1)的通解结构，这里需要利用(1)的两个初值问题解的渐近估计．

先来考虑(1)的第一个初值问题：

问题(2){Bdydx+P(x)y=λy，

引理1 由文献[7]可知，问题(2)的解Φ(x，λ)对λ的渐近式为：

该初值问题解的具体形式在文献[6]中已给出，这里不再赘述．

接着考虑问题(1)的第二个初值问题：

引理2 由文献[7]知，问题(3)的解ψ(x，λ)对λ的渐近式为：

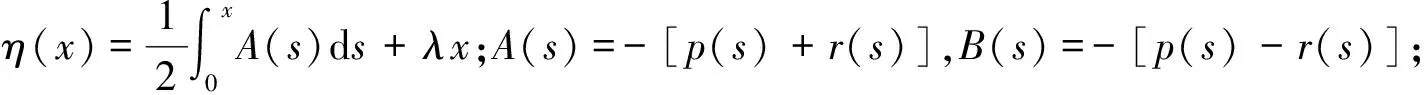
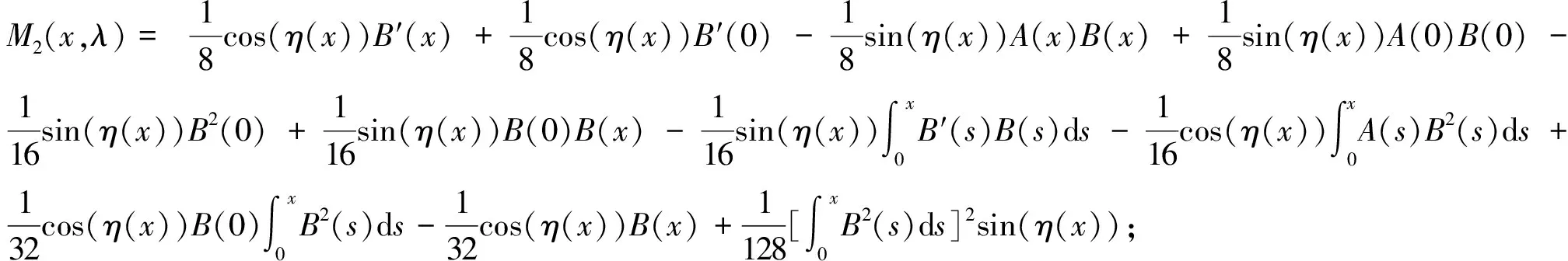
2 决定问题(1)特征值集的整函数

y(x，λ)=c1Φ(x，λ)+c2ψ(x，λ)，c1，c2为常数．

由问题(1)的边界条件知：

(*)

引入关于λ的整函数：

命题1 问题(1)的特征值集合与ω(λ)的零点集合重合．

最后，通过计算对ω(λ)进行渐近估计，这里主要用到定积分计算的分部积分法．

φ2(0，λ)=0，ψ2(0，λ)=1，

所以，整函数ω(λ)关于λ的渐近估计式如下：

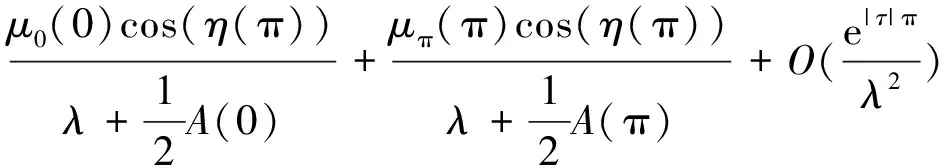
参考文献：

[1] Hurwitz W．An expansion theorem for a system of linear differential equations of the first order[J]．T rans Amer Math Soc，1921(22)：526-543．

[2] Levitan B M，Sargsjan I S. Sturm-Liouville and Dirac Operators[M]．Boston：Kluwer Academic Publishers, 1991．

[3] Levitan B M，Sargsjan I S. Introduction to Spectral Theory, Selfadjoint Differential Operater[M]．Rhode Island：American Mathematical Society Providenee,1975．

[4] 曹策问.非自伴Sturm-Liouville算子的渐近迹[J]．数学学报，1981，24(1)：84-94．

[5] 李梦如.带有非定局边界条件的Sturm-Liouville算子的迹[J]．郑州大学学报：自然科学版，1981(1)：1-7．

[6] 梁银双，夏云青．对带有非局部边界条件的Dirac方程的迹的研究[J]．中州大学学报，2011，28(2)：119-123．

[7] Abdukadyrov E.Calculation of the regularized spur for the Dirac system[J]．Journal of Moscow University， 1967(4)：17-24．