一道微分几何题的一题多解

何 青，邹九生

(江西赣南教育学院，江西 赣州 341000)

一道微分几何题的一题多解

何 青，邹九生

(江西赣南教育学院，江西 赣州 341000)

一题多解对基本概念、基本技巧的把握是有效的甚至是不可替代的途径。分别运用微分解析几何和初等解析几何等方法对一道课本上的微分几何习题从多种角度思考，给出了8种解法。

习题;微分解析几何；初等解析几何；多解

例1 证明曲线x=1+3t+2t2，y=2-2t+5t2，z=1-t2为平面曲线，并求出它所在平面方程。

通过对一个例题从多方位角度思考，能使学生更深理解和区别有关定理和知识，甚至能跨教材联系前后的相关课程。

1 初等解析几何证法

证法1 思路分析如下：任取曲线上2点的切线方向，如果2方向不平行，则可以确定由该2方向所确定的平面的法方向。在曲线上取定已知一点(点确定的向量)，证明该方向垂直于曲线上任意点与已知点确定的向量。由此证明曲线上任一点均落在过已知点且垂直该法向量的平面上。

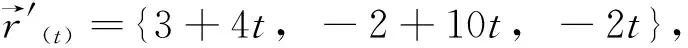
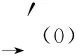
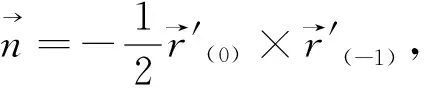
故平面方程为：

(x-1)·2+(y-2)·3+(z-1)·19=0

即：

2x+3y+19z-27=0

证法2 思路分析如下：可以在曲线上任意取出3个特殊点，可以确定这3个点所确定平面的法方向，证明这个法方向与曲线上任意点与该3点中的一点所确定向量垂直。因：

所以：

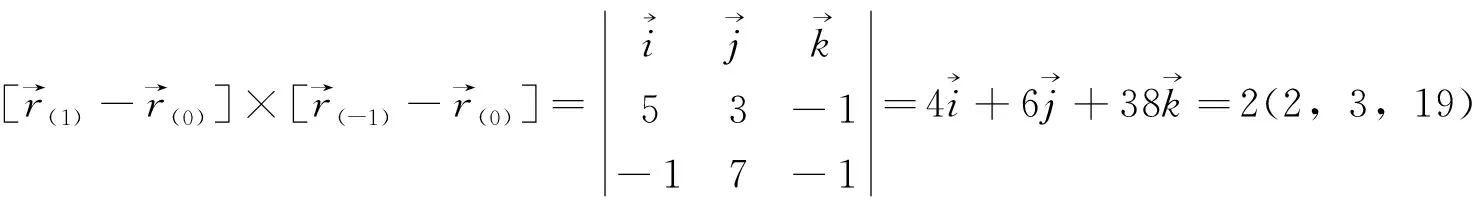
证法3 思路分析如下：消去参数，求出曲线所在平面。由：

消去参数t整理有：

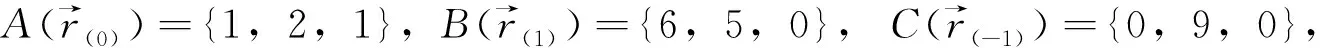
解得：

2x+3y+19z-27=0

2 微分解析几何证法

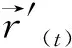
设船舶j相对于船舶i运动的轨迹曲线方程为f(x)，那么船舶i到船舶j的最近距离则可看作是船舶i到曲线f(x)的最近距离见图1。

则：

即这条曲线上任意一点处副法向量是固定向量，从而曲线是平面曲线。

证法6 思路分析如下：根据文献[1]中结论：证明挠率恒等于0的曲线是平面曲线。因为：

由：

即该曲线在任意一点处的挠率恒等于0，曲线是平面曲线，它们所在平面即是曲线在任一点的密切平面。

令t=0，得：

密切平面方程为：

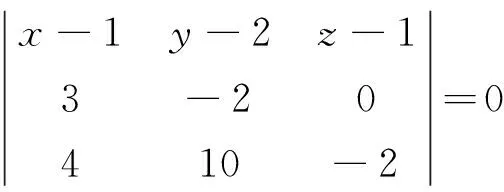
证法7 思路分析如下：直接求曲线上任一点处的密切平面，得到该曲线任一点处的密切平面是固定平面，与参数无关，从而曲线是平面曲线，即密切平面所在平面。令：

则：

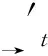
故该曲线在任一点处的密切平面为：

解得方程2x+3y+192-27=0与t无关，该曲线的密切平面不随t的变化而变化，密切平面是固定的，该曲线是平面曲线。

所以可知A、B、C、M共面，即2x+3y+19z-27=0。

3 结 语

上述8种不同解法分别属于微分解析几何和初等解析几何，可以看到具有不同的几何或代数意义，同时在方法上也有不同的一般指导意义。这些方法对提高学生的空间想象能力并加强对几何概念的直观理解有特别作用，同时也让学生集中体会了微分几何和空间解析几何之间的联系。解析几何是微分几何的基础，只有掌握了解析几何的知识和方法，才能更好学习微分几何。一题多解的目的并不在于“多解”,而在于思维的“多层次”,在于学生从多解中分析出解法的优劣,加深对有些概念的透彻理解，同时在于提示教师对有些概念的深层次理解。可以借助于习题的讲解，使学生获得高水平的思维训练,从而提高学生的数学思维能力,培养学生的创新意识。

[1]梅向明，黄敬之.微分几何[M]. 第3版.北京：高等教育出版社，2004.

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.05.044

N4

A

1673-1409(2011)05-0127-03