盘点近年数学高考中的双变量问题

●

(嵊州市教研室 浙江嵊州 312400)

盘点近年数学高考中的双变量问题

●施哲明

(嵊州市教研室 浙江嵊州 312400)

高中数学离不开变量，而变量问题本身就是高中数学的一个难点，涉及到2个变量的数学问题就更难了．相对来说，学生对线性规划中的双变量问题熟悉一些，从近几年高考中的相关题目来看，难度也相对小一些．但也出现了一些新的变化趋势，即需要转化为线性规划问题来解决．而从2010年的数学高考试题来看，对于双变量问题的考查有一种加强的趋势．本文通过近几年数学高考中的双变量问题，谈谈此类问题的解法．

1利用判别式

一元二次方程中的判别式对于高中学生来说并不陌生．利用判别式法求解可以让学生感悟函数与方程的思想，将函数式转变为右边是0的方程．

例1已知平面向量α，β(α≠0,β≠0)满足|β|=1，且α与β-α的夹角为120°，则α的取值范围是________．

(2010年浙江省数学高考理科试题)

分析虽然|β|是确定的，但是2个向量是不确定的，因此也就有|α|的取值范围了．当然利用向量的特殊性，可以用向量的几何意义来解决．这里提供2种利用判别式的解法．

解法1在△ABC中，|OB|=1，且∠A=60°.设|OA|=|α|=x，|AB|=|β-α|=t，由余弦定理可得

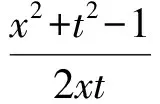
即

t2-xt+x2-1=0(xgt;0,tgt;0).

Δ=x2-4(x2-1)≥0，

解得

解法2利用β=α+(β-α)和α与β-α的夹角为120°，得

1=|α|2+|β-α|2-|α|·|β-α|，

即

|β-α|2-|α|·|β-α|+|α|2-1=0,

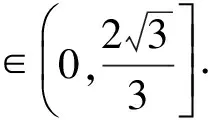
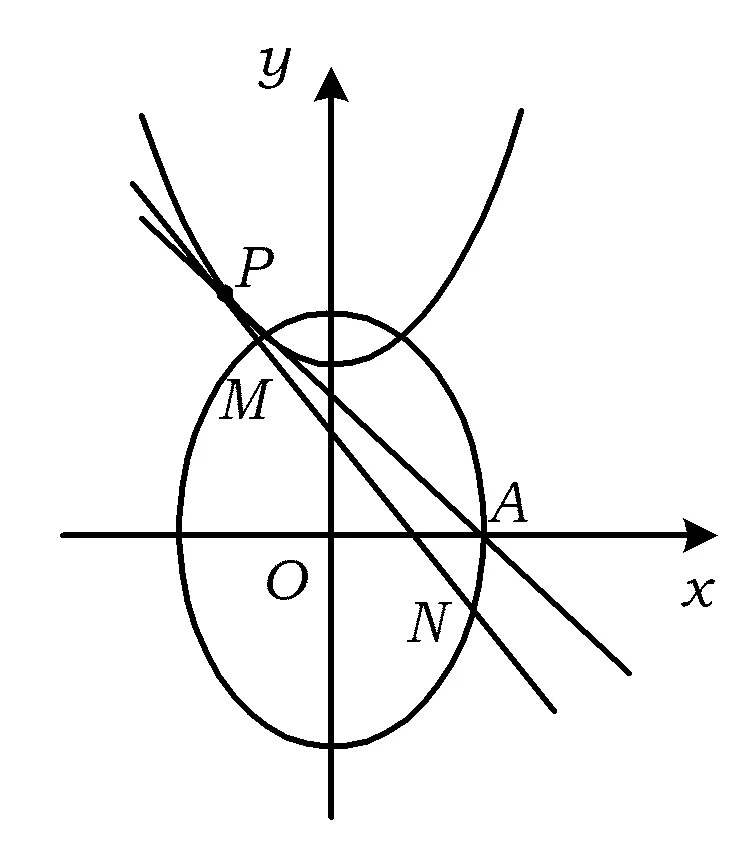
图1

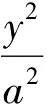
(1)求椭圆C1的方程.

(2)设点P在抛物线C2：y=x2+h(h∈R)上，C2在点P处的切线与C1交于点M,N．当线段AP的中点与MN的中点的横坐标相等时，求h的最小值.

(2009年浙江省数学高考理科试题)

分析(2)根据横坐标相等的条件，可以得到等式t2+(1+h)t+1=0，但从这个等式着手如何求h的最小值呢？由于P是抛物线C2：y=x2+h(h∈R)上的任意一点，因此t∈R，而对于任意的t∈R，方程有解，则应满足判别式大于等于0.

解(1)略.

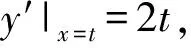
4x2+(2tx-t2+h)2-4=0,

即

4(1+t2)x2-4t(t2-h)x+(t2-h)2-4=0.

因为直线MN与椭圆C1有2个不同的交点，所以

Δ1=16[-t4+2(h+2)t2-h2+4]gt;0.

(1)

设线段MN的中点的横坐标为x3，则

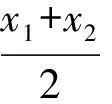
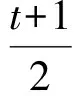
t2+(1+h)t+1=0，

其中

Δ2=(1+h)2-4≥0,

解得

h≥1或h≤-3.

当h≤-3时,

h+2lt;0,4-h2lt;0.

因此不等式(1)不成立，故h≥1.

当h=1时,代入方程t2+(1+h)t+1=0,得t=-1,因此不等式(1)成立，故h的最小值为1．

注：2009年浙江省数学高考文科试题第22题也类似.

例3设a1，d为实数，首项为a1，公差为d的等差数列{an}的前n项和为Sn，满足S5S5+15=0．

(1)若S5=5，求Sn及a1;

(2)求d的取值范围.

(2010年浙江省数学高考文科试题)

分析由S5S6+15=0得

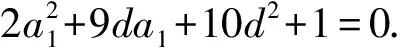
显然，若把上式看成关于d的一元二次方程，也能求出首项a1的取值范围．这也正好反映出它们两者之间的制约关系．

2利用线性规划

高考中的线性规划问题其实也是双变量问题，基于高中学生对这块知识的熟悉程度，仅以2010年江苏省数学高考试题第12题为例予以说明．因为此题很有创意，既可以通过不等式的性质来解决，也可以通过换元转化为线性规划问题来解决，需要通过2边取对数来转化，别有一番新意．

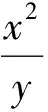
(2010年江苏省数学高考试题)

分析不同于例3，本题出现的是关于变量x,y的不等式，通过不等式相互制约来求目标函数的最值，这容易使我们联想到线性规划的知识．

对已知不等式两边取对数，令lgx=s,lgy=t，则问题可转化为：

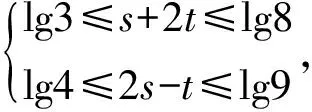
3利用基本不等式

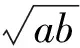
例5若正实数x,y满足2x+y+6=xy，则xy的最小值是________．

(2010年浙江省数学高考文科试题)

分析由已知可以发现，这里的x,y是不确定的，尽管它们相互制约，但是仍然可以看成是一个双变量问题．xy本身在已知中存在，而在已知中还有变量2x,y，如何寻求它们之间的关系就成了解决本题最关键的地方．

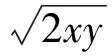
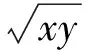
例6已知xgt;0，ygt;0，x+2y+2xy=8，则x+2y的最小值是

( )

(2010年重庆市数学高考理科试题)

分析令x+2y=tgt;0,得

4y2-2ty+8-t=0，

由Δ≥0,得t≥4．

例7已知在半径为2的球面上有A,B,C,D这4个点，若AB=CD=2，则四面体ABCD的体积的最大值为

( )

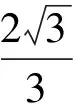
(2010年全国数学高考理科试题Ⅰ)

分析由AB=CD=2，可想到把这个四面体放进一个长方体中.设长方体从一个顶点出发的3条棱的长分别为a,b,c，则

而四面体体积

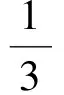
这样就变成了关于a,b的双变量的最值问题，注意到a2+b2为定值，从而就可以用基本不等式求解．

当然，在上述几个例子中都还有双变量之间的一个依赖关系的等式，因此可以把其中的一个变量用另一个变量来表示，那么所求表达式的最值就转换成一个单变量的最值问题了．如例5可以把所求式转换成关y于的一个变量的最值，即求

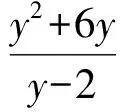
的最值．类似地，在例6中,

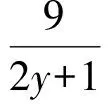
在例7中，

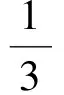
先考虑V2，再结合基本不等式也能求得．

4利用整体思想

整体思想就是从问题的整体性质出发，突出对问题的整体结构的分析和改造，发现问题的整体结构特征，善于用“集成”的眼光，把某些式子看成一个整体，把握它们之间的关联，进行有目的、有意识的整体处理．

( )

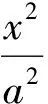
A.3x±4y=0 B.3x±5y=0

C.4x±3y=0 D.5x±4y=0

(2010年浙江数学高考理科试题)

分析过点F2作PF1的垂线，垂足M恰好是线段PF1的中点，因此

|PF1|=4b,|PF2|=2a.

由双曲线定义可知

|PF1|-|PF2|=2a，

于是

2b-c=a.

又由c2=a2+b2，得

4a=3b．

至此,可以发现这里的a,b不是一个确定的具体的数值，而是一个双变量的关系式．而所求的恰好是双曲线的渐进线bx±ay=0，因此可以整体代换而求得．

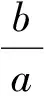
(2010年江苏省数学高考试题)

[1] “2010年高考：数学答题中的优美解及典型失误”征文选登(二)[J]．中学数学教学参考，2010(8):38-59.