基于RLKF的无传感器PMSM控制

高晓波,薛惠锋,谢红普,张 群

(西北工业大学,陕西西安710072)

0 引 言

永磁同步电动机(以下简称PMSM)因其结构简单、效率高、体积小等优点而广泛应用于航空、航天、工业自动化等领域。目前,PMSM高性能控制系统需要在转子上安装传感器(如编码器、测速发电机等)以反馈转子的位置和转速;但是,位置传感器的性能易受潮湿、高温、震动等恶劣环境影响,存在安装和维护的困难,且机械传感器增加了系统成本和复杂性。

近年来,国内外众多学者对电机的无传感器控制进行了广泛的研究,取得了大量成果,提出了几种具有典型意义的方法,主要有扩展卡尔曼滤波算法[1]、滑模变结构观测器法、模型参考自适应法(MARS)以及高频注入法。扩展卡尔曼滤波器法(以下简称EKF)对电机转子位置和转速进行估计,是最小二乘的最优估计,它能有效地削弱随机干扰和量测噪声的影响,其输出能很快跟踪系统实际状态。但该算法需要求逆矩阵,计算量大,协方差阵的初值选择只能试凑,耗时长[2]。针对上述扩展卡尔曼滤波器法的缺点,本文重新构建PMSM的降阶状态方程,采用正交的输出变量,设计了一种降阶线性卡尔曼滤波算法,实现了PMSM的无传感器矢量控制。方法简单易行,易于实现。

1 PMSM数学模型

首先假设:

(1)忽略空间谐波,电机三相定子绕组在空间对称分布,所产生的磁动势沿气隙圆周按正弦规律分布,忽略磁场的高次谐波分量;

(2)磁饱和及铁心损耗忽略不计;

(3)电机定子绕组的反电势是正弦波,转子与定子绕组之间的互感是转子位置角的正弦函数。

在静止的α-β坐标系,表贴式PMSM方程[3]表示:

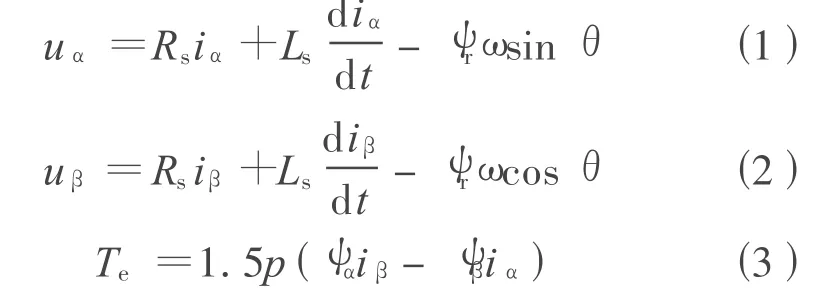
式中:uα、uβ为定子α、β轴的电压;iα、iβ为定子α、β轴电流;Rs为定子电阻;Ls为同步电感;ψr为永磁体磁链;ω为转子机械角速度;θ为转子机械位置;p为电机极对数。

2 经典扩展卡尔曼滤波(EKF)理论

PMSM的数学模型是一个电磁参数强耦合的非线性系统,选取状态变量x=[iαiβωθ]T,u=[uαuβ]T,y=[iαiβ]T,得到系统状态方程:

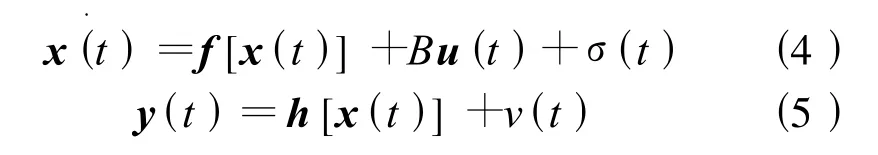
式中:σ(t)为系统过程白噪声;v(t)为量测过程白噪声。根据扩展卡尔曼滤波理论,小采样时间的条件下,求系统矩阵的雅克比矩阵可得到最优估计点附近的近似线性化模型,再对状态方程进行离散化,得到卡尔曼滤波的目标离散系统[4]。代入EKF滤波方程,EKF滤波算法分两个阶段:

(a)预测阶段:

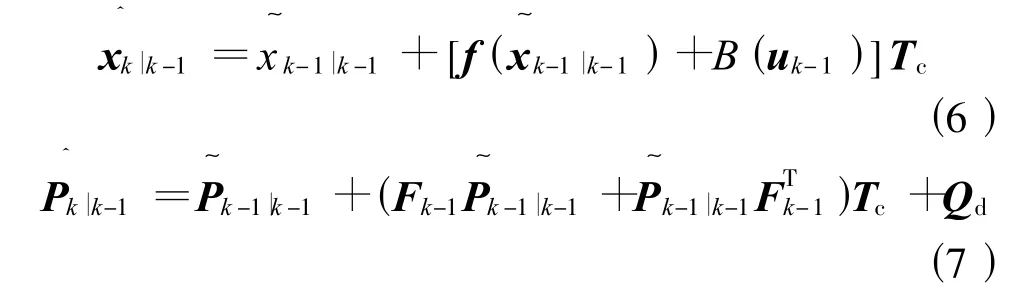
(b)修正阶段:

由于雅克比矩阵Fk是时变矩阵,所以每个采样时刻都需要计算协方差矩阵,计算量大。且Q、R、P0阵的选取对算法收敛及稳态性能影响很大,其选取一般采用试凑方法,需多次反复试验。

3 降阶线性卡尔曼滤波算法(RLKF)

上述EKF算法计算量大的主要原因是系统雅克比矩阵为时变矩阵,若系统矩阵为常数矩阵,则协方差阵可收敛至常阵,可简化卡尔曼滤波算法。重新选取状态变量x=[θ ω ρ′],θ为转子位置,ω为转子转速,ρ′为高斯白噪声ρ的一阶导数,这样的状态变量选取可以使Kal man滤波器跟踪斜坡速度变化[5]。取转子位置信号的正弦和余弦函数为输出信号,建立系统差分方程:

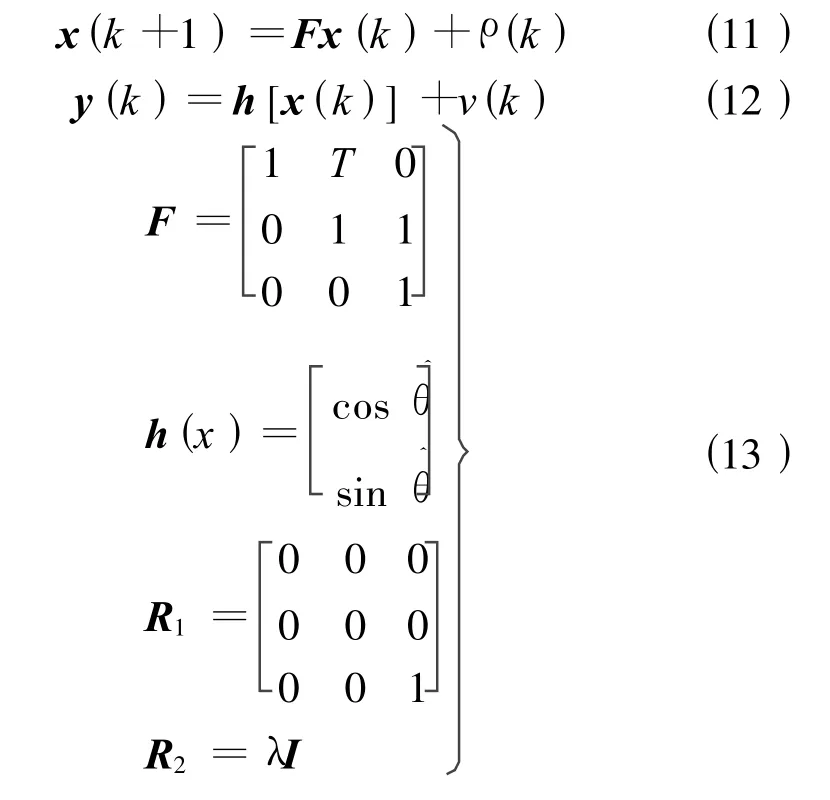
式中:ρ(k)为系统噪声矩阵;v(k)为量测噪声;R1为系统噪声协方差阵;R2为量测噪声协方差阵;T为滤波算法的离散采样时间。通过调节参数λ可以调整系统抗干扰能力。应用扩展Kal man滤波法求系统状态变量x(k)的最优估计[6],先对输出矩阵求导得雅克比矩阵:

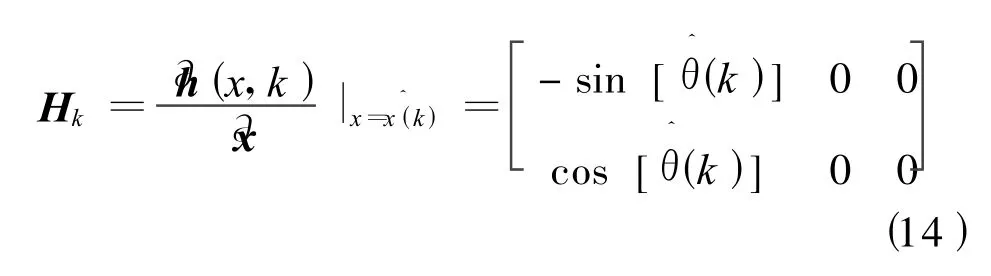
令:

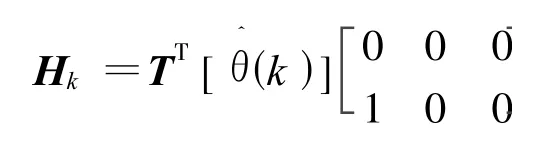
Pk为时不变矩阵,可收敛至常数矩阵Kal man增益Kk简化:

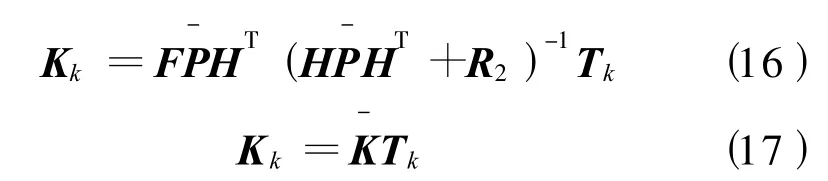
由H矩阵首行为全为零可知:

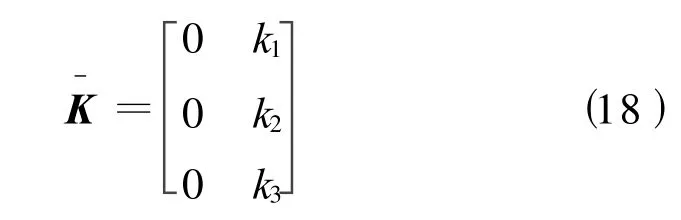
由于定子直、交轴磁链值与位置信号的三角函数值成比例,本文选用静止α-β坐标系定子磁链代替位置信号的三角函数[7]。a为位置信号三角函数值与定子磁链的比例系数。输出方程可表示:

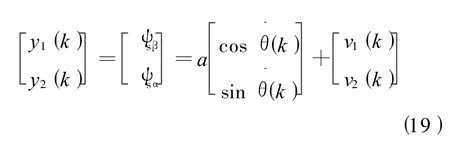
经过以上变换,扩展卡尔曼滤波器(EKF)转化为降阶线性卡尔曼(RLKF)滤波器:

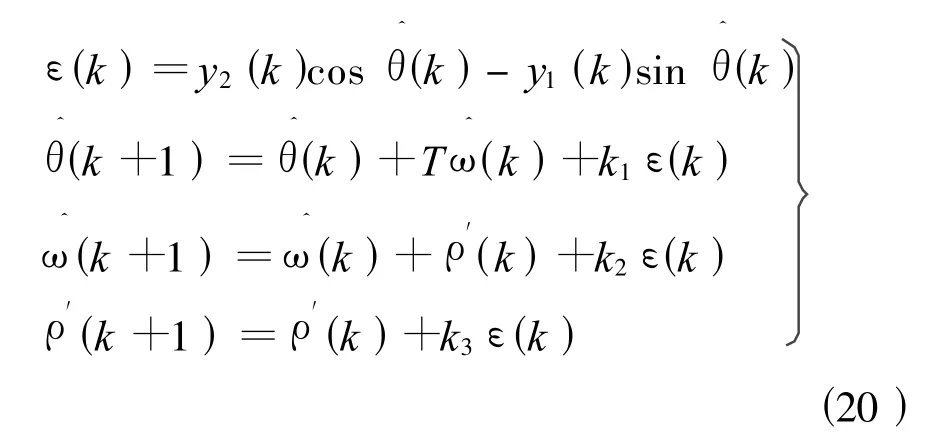
该算法在一个采样时刻内仅需要做6次乘法运算和两次三角函数运算,与EKF算法相比,运算量显著减小。

4 仿真验证

本文的仿真实验是在Matlab 7.0的Simulink环境下完成的。控制策略选用磁链定向电流转速双闭环PI控制,采用空间矢量脉宽调制(SVPWM)方法,控制方式采用。表1为PMSM参数。

表1 PMSM参数

设定RLKF的取样时间为T=0.01 s,通过试凑,λ=5 000时,系统的位置跟踪能力及抗噪声能力较为平衡。协方差矩阵P收敛至常数矩阵:

图1为LKF对转子位置估值与转子实际位置的误差分析,由图1可知,电机在0.3 s时进入稳态,稳态误差几乎为零。图2为RLKF对转速的估计曲线,从图2中可以看出,0.3 s时稳定至给定转速700 r/min,稳态误差同样几乎为零,表明了RLKF有较好的稳态性能。图3、图4分别为直、交轴计算得磁链与实际位置信号的正三角函数值的比对曲线,两者成正比例关系。图5、图6分别为电机定子三相电流及电机旋转坐标系电流Iq,由图6可知,在负载转矩突变的情况下,系统具有快速稳定的调节能力,具有良好的动态性能。

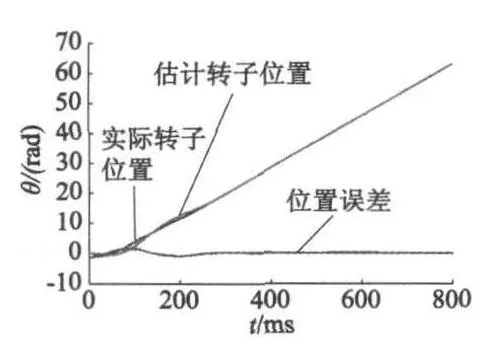
图1 转角跟踪曲线

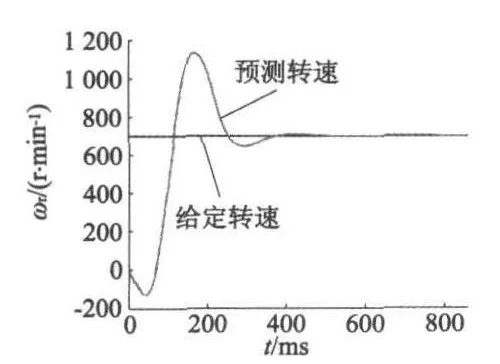
图2 转速跟踪曲线

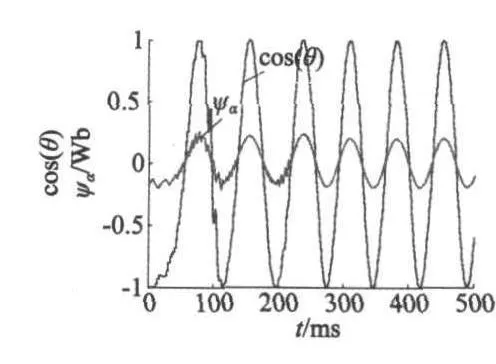
图3 α轴磁链及cos θ

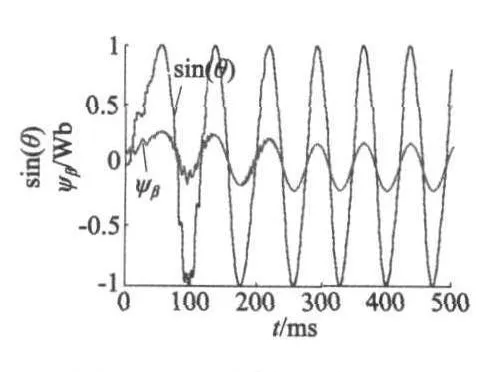
图4 β轴磁链及sin θ

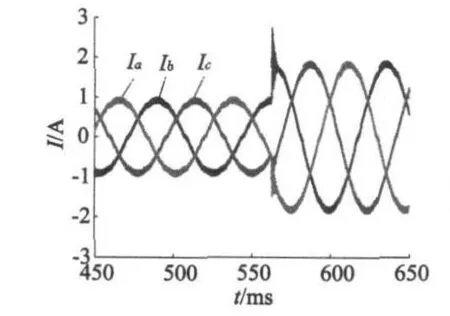
图5 阶跃变负载下的三相电流

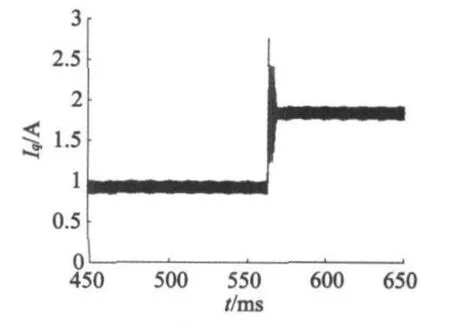
图6 旋转坐标系q轴电流

5 结 语

本文在经典扩展卡尔曼滤波算法的基础上,应用降阶线性卡尔曼滤波算法对PMSM进行无传感器控制。仿真实验验证了该算法的可行性,计算量较经典卡尔曼算法大大减少。对转子的转速和位置估计精度高,位置和速度响应快,是一种性能优良的无传感器控制方法。

[1] Welch G,Bishop G.An Introduction to the Kal man Filter[EB/OL].TR 95-041,2006.http//www.cs.unc.edu/～welch/kal man/kal manIntro.html.

[2] 李玉忍,谢利理,齐蓉,等.永磁同步电机无位置传感器调速系统的研究[J].西北工业大学学报,2003(8):428-431.

[3] 阮毅,陈维均.运动控制系统[M].北京:清华大学出版社,2005.

[4] 吴永前,李玉忍.扩展Kal man滤波在永磁同步电机无速度传感器调速系统中的应用[J].电气传动自动化,2001(12):3-6.

[5] Huang M C,Moses A J.Linear Kal man Filter(LKF)Sensorless Control for Permanent Magnet Synchronous Motor Based on Orthogonal Output Linear Model[C]//International Symposium on Power Electronics,Electrical Drives,Automation and Motion.2006:1381-1386.

[6] Harnefors L.Speed Estimation From Noisy Resolver Signals[C]//Sixth International Conference on Power Electronics and Variable Speed Drives.1996:279-282.

[7] Huang M C,Moses A J.Reduced-Order Linear Kal man Filter(RLKF)Theory in Application of Sensorless Control for Permanent Magnet Synchronous Motor(PMSM)[C]//IEEE Conference on Industrial Electronics and Applications.2006:1-6.