一个组合恒等式的多种证明方法
2011-11-18汪冶华
汪冶华
新疆师范大学数学科学学院,新疆 乌鲁木齐 830054 乌鲁木齐职业大学基础教育部,新疆 乌鲁木齐 830001
一个组合恒等式的多种证明方法
汪冶华
新疆师范大学数学科学学院,新疆 乌鲁木齐 830054 乌鲁木齐职业大学基础教育部,新疆 乌鲁木齐 830001
组合恒等式是组合数学的一个重要部分。用数学归纳法、组合分析法、概率分析法、几何法、母函数法等方法来证明一个常见的组合恒等式,并从母函数法得到Vandermonde恒等式,同时提出了WZ方法来证明组合恒等式。
组合恒等式;数学归纳法;组合分析法;概率分析法;几何法;母函数法
在组合数学中,表示组合数之间关系的恒等式称为组合恒等式。它在数学的各个分支中都有广泛应用,并且其证明方法多种多样,具有很强的灵活性。因此,组合恒等式的证明方法是值得研究的课题。应用组合数的定义和性质去证明组合恒等式是最常见的方法。下面笔者讨论了用数学归纳法、组合分析法、概率分析法、几何法、母函数法等方法来证明一个常见的组合恒等式:
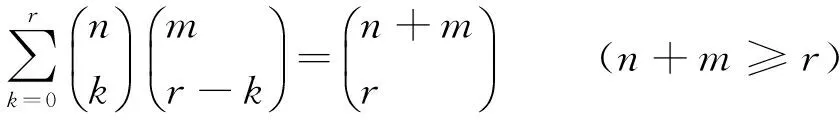
(1)
并从母函数法得到Vandermonde恒等式,同时提出了WZ方法来证明组合恒等式。
1 证明方法
1.1组合分析法
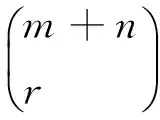
组合分析法主要就是利用组合知识说明等式两边的式子都是对同一组合问题的计数。具体步骤就是先由恒等式中意义比较明显的一边构造一个组合问题的模型,再根据加法原理或乘法原理对另一边进行分析。若是几个数(组合数)相加的形式,可以把构造的组合问题进行适当分类,若是几个数(组合数)相乘的形式,则应进行适当的分步计算,很多情况下是两者结合使用的。
1.2概率分析法
构造一个概率模型:书架上有n本文学类书,m本医学类书,从中任取r本,令随机变量X表示所取到的文学类书,则:
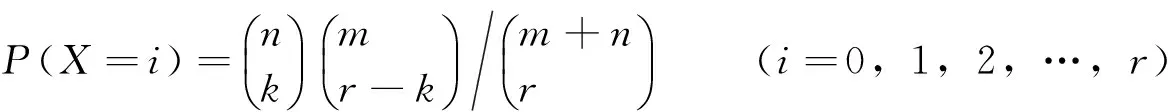
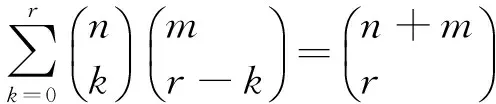
1.3数学归纳法
对n进行归纳。
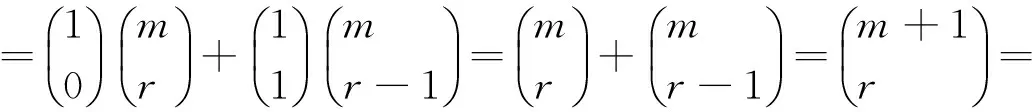
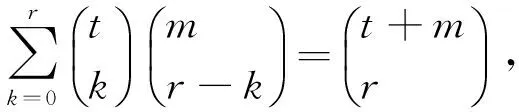
n=t+1时,则有:
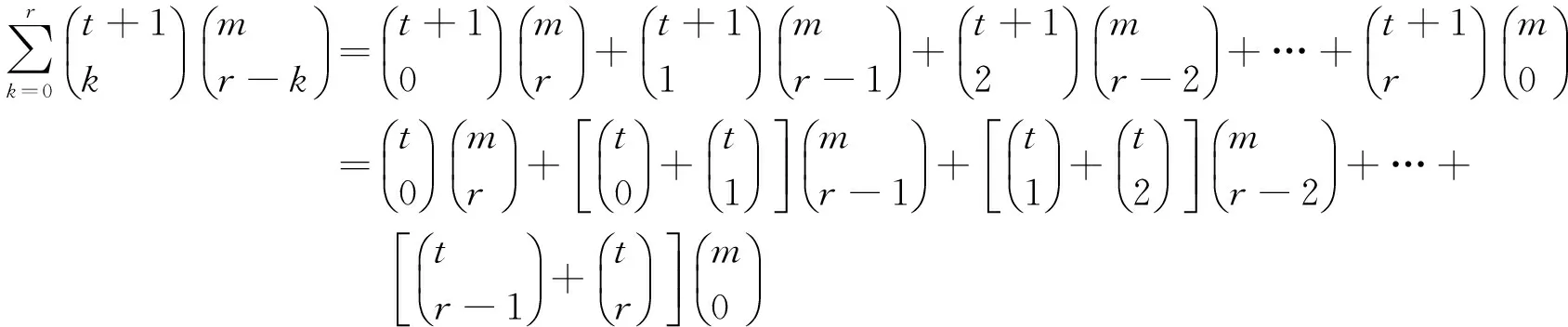
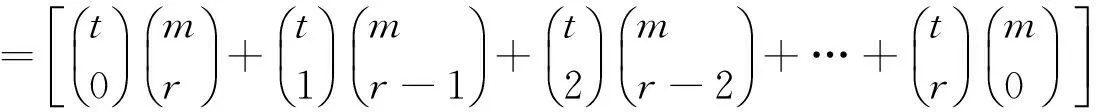
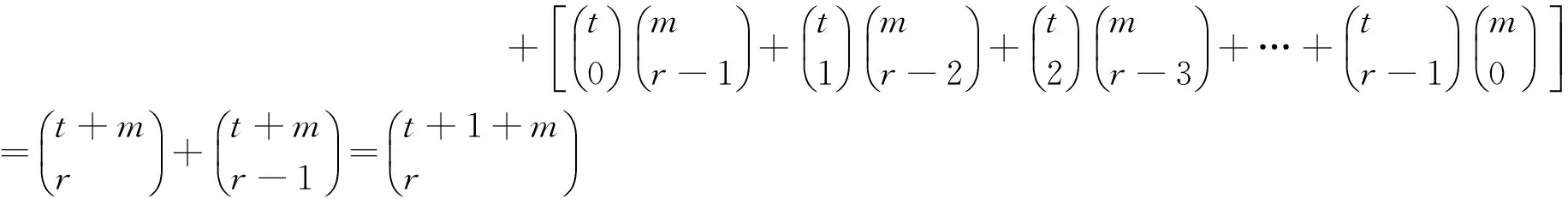
所以n=t+1时,等式成立。
1.4几何法
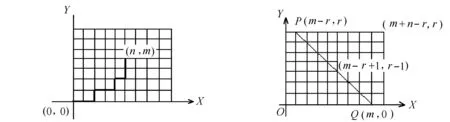
图1 从点(0,0)到(n,m)的路径数 图2 从点(0,0)到(m+n-r,r)的路径数
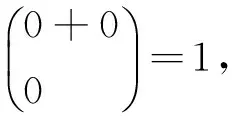

1.5母函数法
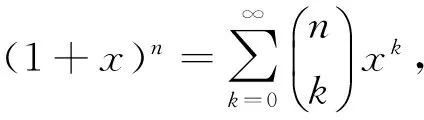
所以:
对比xr的系数得:
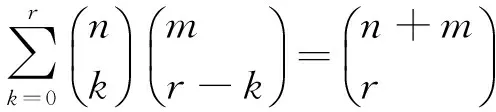
2 Vandermonde恒等式和WZ方法
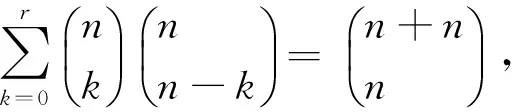
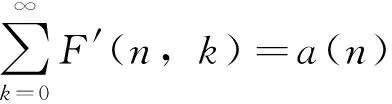
G(n,k)=R(n,k)F(n,k)
(2)
则有下列WZ方程成立:
F(n+l,k)一F(n,k)=G(n,k+1)一G(n,k)
(3)
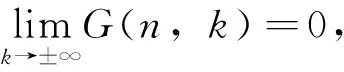
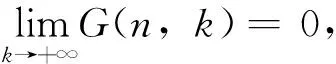
若(由计算机)找不到这样的有理函数,并不能说明要证明的恒等式不成立,此时可以考虑使用其它方法给予证明。由此发现,WZ方法在证明求和恒等式时是很有效的,其最大优势在于高度算法化,Maplel2和Mathematica6.0都有相关的程序包。在证明较复杂的超几何恒等式时,WZ方法显然是比较简便的。
[1]陈福泰,李群.组合恒等式的几何证法[J].数学教育,1989(1):8-10.
[2]曹汝成.组合数学[M].广州:华南理工大学出版社,2000.
[3]黄均振,褚玉明.若干2 F1型超几何级数恒等式的WZ方法证明[J].湖州师范学院学报,2009,31(1):30-33.
[编辑] 洪云飞
10.3969/j.issn.1673-1409.2011.03.003
O157
1673-1409(2011)03-0007-03
