民用爆炸物品运输网络节点选址研究*
2011-11-15刘义新
吴 颖,刘义新
(1.湖南交通职业技术学院, 湖南长沙 410004;2.长沙市公安局, 湖南长沙 410005)
民用爆炸物品运输网络节点选址研究*
吴 颖1,刘义新2
(1.湖南交通职业技术学院, 湖南长沙 410004;2.长沙市公安局, 湖南长沙 410005)
以安全风险分析为重点,同时考虑服务时间和投资成本等因素,建立多目标多层次的民用爆炸物品运输网络节点选址模型,并利用混合遗传算法求解。通过算例证明,该方法规划的爆炸物品运输网络节点,能够降低爆炸物品对环境安全造成的影响,提高运输的效益。
安全风险;爆炸物品;运输网络;选址模型;混合遗传算法
民用爆炸物品运输事故的发生,给社会及生态环境带来严重的影响,也给人民生命财产和企业经济带来了巨大的损失。因此,运用科学的方法来辅助运输管理就变得非常迫切。对于爆炸物品的运输管理,即设计爆炸物品运输网络,其中最重要的就是构建运输网络的节点选址。
1 民用爆炸物品运输网络节点选址风险因素分析
选址风险因素主要包括:选址周围环境、事故影响区域、救援能力。
1.1 选址周围环境
民用爆炸物品配送中心属于高危险设施,按照国家标准,配送中心的建筑必须依山而建,进而降低爆炸冲击波的影响。所以本研究的选址周围环境主要以备选地址周围地形作为考虑的依据。选址周围环境影响系数α为:

式中:α——备选地址周围环境影响系数;
β——备选地址周围山体高度影响系数;
γ——备选地址周围山体坡度影响系数,其中 ,β,γ的选取见表1。
1.2 事故影响范围
本研究对于民用爆炸物品的事故影响范围,主要考虑民用爆炸物品爆炸或燃烧对周围人员生命的影响。设备选地址发生事故的概率为 P,事故影响以λ为直径的圆形区域,λ由民用爆炸物品的类型、数量确定。所以备选地址事故影响范围的人口为:

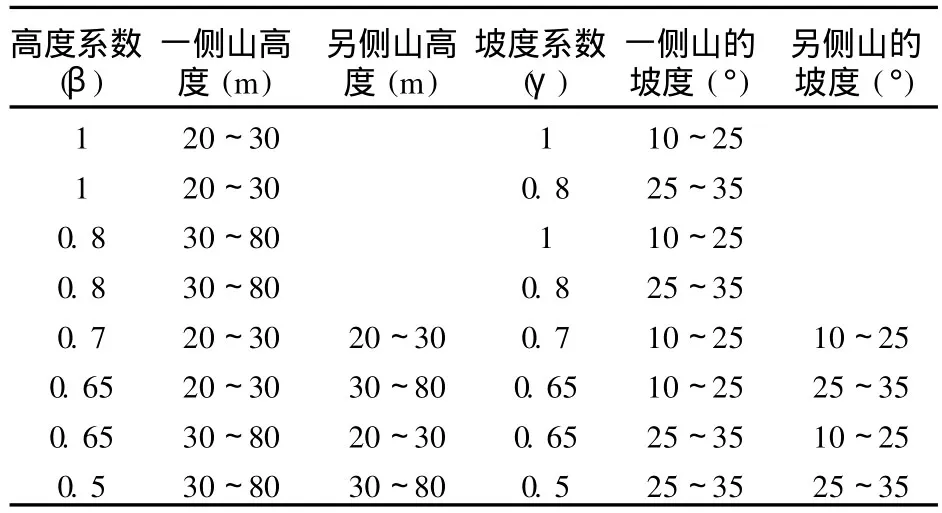
表1 选址周围环境影响因素
式中:C——选址区域发生事故影响的总人数,万人;
ρ——选址区域周围的人口密度,万人 /km2;
λ——事故影响的直径,km。
1.3 救援能力
救援能力主要是指消防设施和医疗设施这 2个因素对减轻爆炸事故后果所产生的积极影响[3]。
(1)消防因素。消防因素主要从距离和容量两个方面考虑。消防设施距离备选地址小于等于 5 km,δ1设置为 0.8;消防设施距离备选地址大于 5 km小于 20 km,δ1设置为 0.95;消防设施距离备选地址大于 20 km,δ1设置为 1.25;设施拥有消防车辆小于 3台,δ2设置为 1;设施拥有消防车辆大于 3台小于 5台,δ2设置为 0.95;设施拥有消防车辆大于 5台 ,δ2设置为 0.85。
则消防因素的参数模型为:

(2)医疗因素。医疗因素主要从距离和容量两个方面考虑。医疗设施距离备选地址小于等于 5 km,ε1设置为 0.8;医疗设施距离备选地址大于 5 km小于 20 km,ε1设置为 0.95;医疗设施距离备选地址大于 20 km,ε1设置为 1.25;设施救护车辆小于 3台,ε2设置为 1;设施拥有救护车辆大于 3台小于 5台,ε2设置为 0.95;设施拥有救护车大于 5台,ε2设置为 0.85。所以医疗因素的参数模型为:

综合以上 2个因素的影响,救援能力的参数模型为:

式中:H——备选地址的救援能力系数。
通过对选址周围环境、事故影响的范围以及救援能力的分析,并建立了相应的参数模型,最终可以得到民用爆炸物品运输网络节点选址风险模型:

式中:R——民用爆炸物品运输网络节点备选地址的风险值;
P——备选地址发生事故的统计概率。
2 民用爆炸物品运输网络节点选址模型的构建
本研究将民用爆炸物品运输网络节点的层次分为地方运输节点、区域运输节点和中央运输节点等级别层次。一般中央运输节点的规模最大,配送批量大,通常只为少数的大用户或者区域运输节点服务,由于其量大,所以比较重视降低成本;区域运输节点和地方运输节点的规模就比较小,配送批量也小,尤其是地方运输节点规模小,要求“小批量、多频次”的配送,对时间的控制更严,但是这 3个层次的运输节点对于安全风险控制的要求都非常高。
2.1 影响建模的其他因素
(1)运输量因素。包括客户的需求量、供应的数量、民用爆炸物品分类等,这些数据会随着时间变化而出现波动。
(2)成本因素。包括各节点之间的运输成本,运输节点所在地的土地成本、建设投资、设备投资及劳动力成本等。
(3)时间因素。包括供应商至运输节点的运输时间、运输节点至客户的配送时间、运输节点之间的配送时间;供应商到运输节点在规定时间内的到达率、运输节点至客户在规定时间内的到达率;运输节点对需求的响应时间、客户要求的响应时间。
(4)其他因素。供应商的位置、客户的位置,以及各个运输节点候选地址的运输距离。本研究采用的是折现距离 (Rectilinear Metric),也叫做城市距离。由于实际路线中,几乎不存在完全的直线形式,所用折现距离等于欧几里德距离乘以一个适当的修正系数φ,在我国φ一般取值为 1.4~1.6。
2.2 建立多级运输网络节点选址模型
(1)地方运输节点选址模型为:
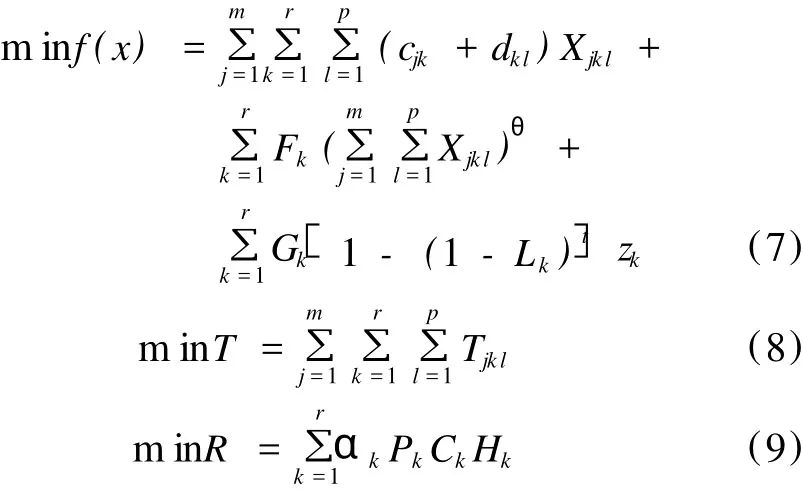
式中,m——供应商数量,即 j=1,2,…,m;
r——运输节点的数量,即 r=1,2,…,r;
p——需求点个数,即 p=1,2,…,p;
t——运输节点的服务年限;
cjk——从供应商 j到运输节点 k的单位运输成本;
dkl——从运输节点 k到需求点 l之间的单位运输成本;
Xjkl——从供应商 j经过运输节点 k到需求点 l的运输量;
θ——运输节点 k的变动费用与运输量的相关系数;
Fk——运输节点 k的单位变动成本;
Gk——运输节点 k的固定资产投资费用;
Lk——运输节点 k的固定资产的年折旧率;
zk——0~1变量,当使用运输节点 k时,取值为 1,否则,取值为 0;zkl是 0~1变量,当运输节点 k为需求点 l服务时,取值为 1,否则,取值为 0;
μikl——运输节点 k到达需求点 l的准时率;
ol——需求点 l要求的准时到达率;
Tjkl——供应商 j经过运输节点 k中转到达需求点 l的响应时间;
Ql——需求点 l的需求量;
Wk——运输节点 k的最大容量;
Aij——供应商 j的最大供应能力。
(2)区域运输节点选址模型。由于该节点要求上级节点补货的批量和频率都较之客户直接对运输节点的要求低很多,而且运输节点内还会有一定的库存量,因此可以不考虑时间影响。模型如下:

式中:k——地方运输节点;
k2——区域运输节点;
r2——区域运输节点的个数,即 k2=1,2,…,r2;
r1——地方运输节点的个数,即 k=1,2,…,r1;
t1——区域运输节点服务年限。
(3)中央运输节点选址模型。这一级运输节点选址在考虑安全风险因素的前提下采用重心法。
3 利用混合遗传算法求解模型
遗传算法作为一种全局搜索优化算法,在遇到包含多个局部最优值的多峰函数问题时,往往能成功地避开局部最优的陷阱,但是求解到一定范围时,会出现大量冗余,导致对求解过程中对于优化信息的反馈不足。蚁群算法主要是通过蚁群之间迅速的信息反馈使问题的解达到最优,但是算法初期信息量缺乏,导致求解速度慢。将遗传算法与蚁群算法结合,能够充分发挥遗传算法的快速全局搜索和蚁群算法信息反馈迅速的能力,运算流程如图1所示。

图1 混合遗传算法运算流程
4 算 例
本文拟定某民用爆炸物品运输网络节点的使用年限为 15 a,假设该爆炸物品运输网络拥有 26个需求区域,目前该运输网络的年运输费用是 500万元,平均配送准时率为 86%,在一些偏远地区的准时率甚至在 70%以下。安全风险影响因素、及时到达率和一次性建设成本根据实际情况确定,安全风险值小于 130为合理范围;各需求点的平均需求量已知;地方运输节点备选点与需求区域之间的单位运输成本,参考国家交通部发布的《汽车运价规则》和行业水平。
通过Matlab计算,最终获得该算例的一组优化结果见表2。所有被选地址的安全风险值均在合理范围。建设多层次的配送中心网络后年运输成本是277.7210万元,平均配送及时率达到 97.5%。年运输成本的结余 44.46%,即使是考虑到配送中心建设一次性投资 3000万元,仍具有很好的经济效益。
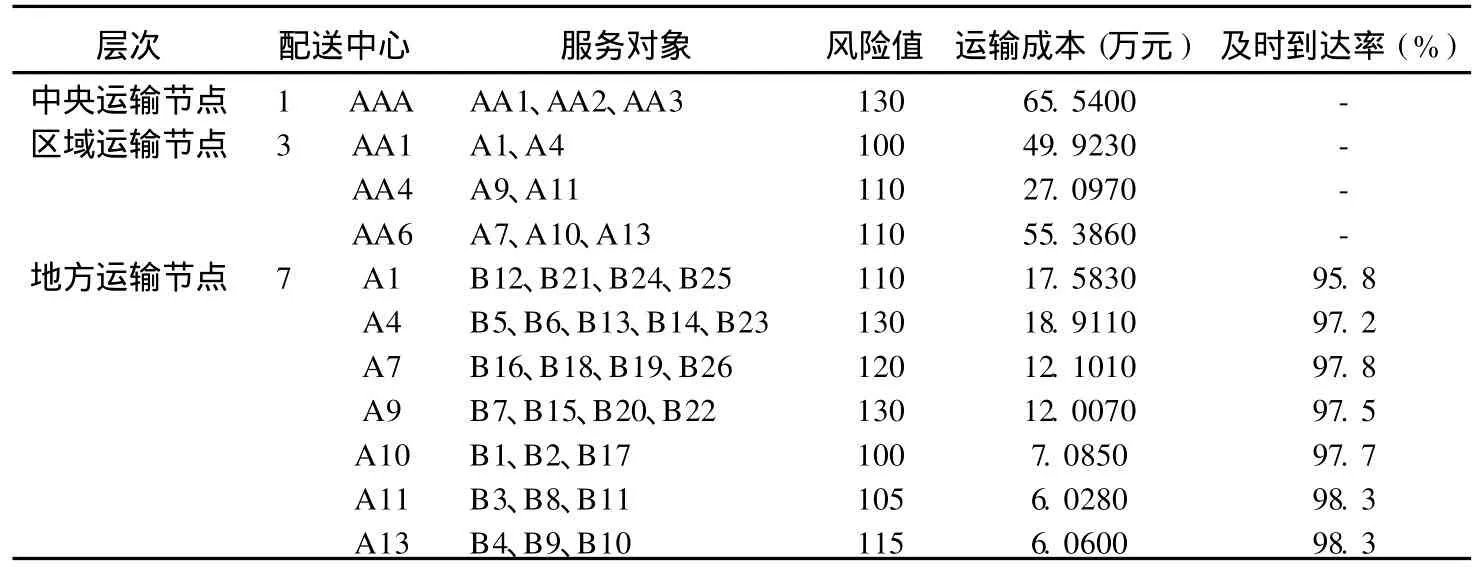
表2 最终选址结果
5 总 结
本文在解决民用爆炸物品运输网络节点选址问题上,具有以下优势:
(1)通过改进运输节点选址模型加入考虑安全风险和及时到达率 2个重要的影响因素,建立更加符合爆炸物品运输网络节点要求的多层次选址模型;
(2)将运输网络节点选址进行层次划分,更有效的提高运输效率降低运输成本;
(3)本文采用遗传算法和蚁群算法相结合的混合遗传算法求解模型,能够更加快速的求出最优解,降低民用爆炸物品的运输网络的风险。
[1] 郜振华.遗传算法在有竞争的物流配送中心选址中的应用[J].公路交通科技,2005,22(8):138-141.
[2] 韩庆兰,梅运先.基于BP人工神经网络的物流配送中心选址决策[J].中国软科学,2004,(6):140-143.
[3] 吴 颖,程赐胜.基于 SOM神经网络的民用爆炸物品配送中心选址决策[J].长沙交通学院学报,2007,23(3):34-38.
[4] 吴 颖,程赐胜.易燃易爆物品道路运输路径选择问题研究[J].交通科学与工程,2009,25(4):97-102.
[5] 程赐胜,苏玲利.DEA法在物流中心选址中的应用[J].长沙理工大学学报,2004,1(3,4):8-12.
[6] 汪旭光.爆破安全规程实施手册[M].北京:人民交通出版社,2004.
湖南省教育厅高等学校科学研究项目(11C0493).
2011-07-06)
吴 颖 (1983-),男,湖南长沙人,讲师,博士生,从事交通运输规划与管理研究,Email:763974151@qq.com。
