海量卫星重力梯度观测数据确定地球重力位模型的数值方法*

朱广彬 常晓涛 邹贤才 徐新禹 王建强

(1)国家测绘局卫星测绘应用中心，北京 100830 2)武汉大学测绘学院，武汉 430079 3)东华理工大学测绘工程学院，抚州344000)

海量卫星重力梯度观测数据确定地球重力位模型的数值方法*

朱广彬1)常晓涛1)邹贤才2)徐新禹2)王建强3)

(1)国家测绘局卫星测绘应用中心，北京 100830 2)武汉大学测绘学院，武汉 430079 3)东华理工大学测绘工程学院，抚州344000)

基于空域最小二乘法，对卫星重力梯度数据确定地球重力场中的Cholesky分解法、预条件共轭梯度法以及OpenMP并行算法3种数值方法进行比较与分析。研究表明，在计算机硬件资源有限的情况下，传统的Cholesky分解法已经无法满足求解要求;预条件共轭梯度法的求解效率较之Cholesky分解法有改进，但其以损失小量精度为代价;OpenMP并行算法在不损失求解精度的条件下，可提高求解的效率。

卫星重力梯度;Cholesky分解;预条件共轭梯度;OpenMP并行算法;数据处理

1 引言

地球重力位模型一般采用球谐系数进行表达。基于空域最小二乘法或时域最小二乘法［1-5］，利用卫星重力梯度数据确定地球重力场时，随着求解阶数的增加，未知数个数呈平方倍增长。因此，如何对海量数据进行快速有效的数值处理是需要重点考虑的内容。一般来讲，有以下3种处理方式：方程组的直接解法，例如Cholesky分解法、矩阵QR分解法等。此种方法经过有限次运算能够获得方程的精确解，但是总的运算量和运算时间并没有得到优减，故而该方法在求解大型方程组时实用性较差。第二种是方程组的迭代解法，即通过构造一个向量的无穷序列，其极限对应了方程组的精确解，从某一初始解开始，通过逐次迭代，逐渐收敛至真解。该类方法在有限迭代次数内，无法得到精确解和精度信息，但运算时间大大缩减。共轭梯度法、最速下降法、预条件共轭梯度法(PCCG)等均属于该类方法的范畴。第三种方法是基于并行计算思想，充分发挥计算机硬件结构特点，对直接解法的计算结构进行优化组合，从而提高程序的执行效率。本文将对Cholesky分解法、预条件共轭梯度法、OpenMP(Open Multi-Processing)并行解法进行数值分析和比较。

2 方法介绍

2.1 Cholesky分解法

基于空域最小二乘法或者时域最小二乘法，利用卫星重力梯度数据恢复地球重力场时，均可以化为［3-6］：

其中，法方程N=ATPA满足正定对称特性，W= ATPl，A为设计矩阵，P为权阵，l为观测向量，因此可以利用Cholesky分解法进行直接求解。

2.2 PCCG方法

共轭梯度法的基本思想是利用迭代求得的增量改正上一次迭代的初始向量，所得结果作为下次迭代的初值。增量方向取逼近其解的最速化方向，且利用上一次的初始向量和增量按此梯度方向更新增量。为了进一步提高迭代的收敛速度，可以选择一个预条件阵Nbd应用到共轭梯度方法中，该矩阵的逆要求便于计算，且与法方程矩阵的乘积的条件数要小于法方程矩阵自身的条件数，即：

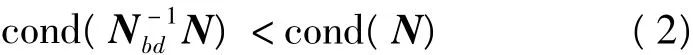
PCCG方法的具体计算步骤如下［7］：

1)选择参数初值x0==0，计算残差向量与方向向量的初值为预条件矩阵逆阵，k=0;

3)计算新的参数向量xk+1=xk+αkpk;

4)计算新的残差向量rk+1=rk-αkak;

8)k=k+1，回到迭代步骤2)。

前后两次迭代解向量的差利用

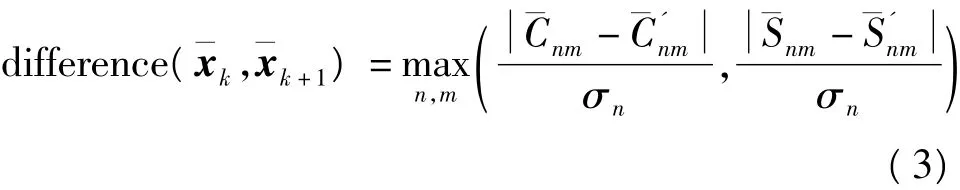
2.3 OpenMP并行编程模型

OpenMP采用Fork-Join并行执行模型［8］。当程序开始执行时只有主线程存在，主线程会一直串行的执行;当遇到需要并行计算的并行域时，主线程会创建一队并行的线程开始并行执行;当派生线程在并行域中执行完毕后，它们退出或者挂起，此时只有主线程在运行(图1)。OpenMP应用编程接口可以根据不同并行域的需要动态地改变线程数，且该并行结构可以嵌入到别的并行结构中去。从本质上讲，OpenMP的并行化是通过使用嵌入到源代码中的编译制导语句来实现的，其是一个外部编程模型，而不是自动的编程模型。

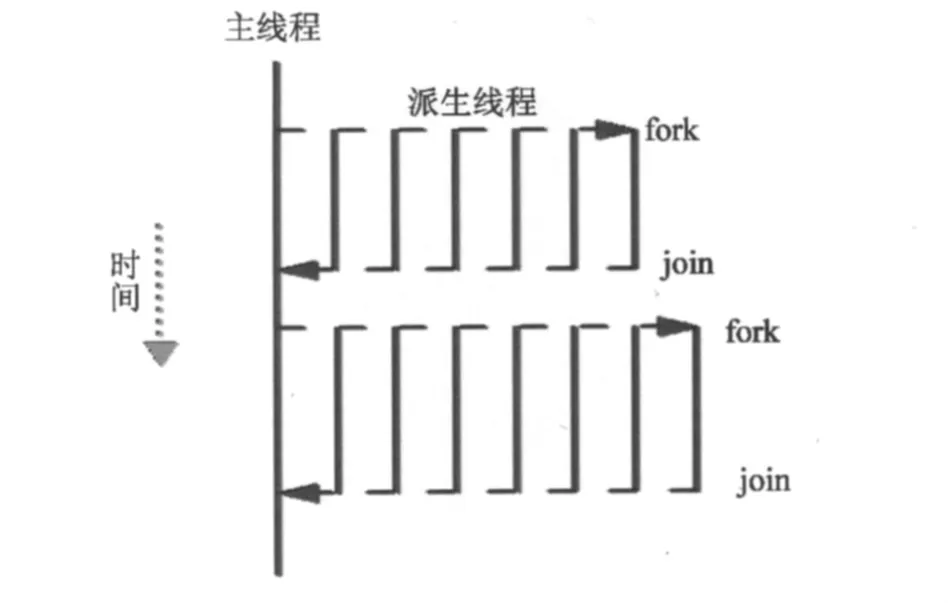
图1 OpenMP并行执行模式Fig.1 OpenMP parallel execution mode

并行算法的加速比与效率是并行算法的两个重要指标，其表征了使用并行算法求解实际问题所能获得的好处［9］。并行算法的绝对加速比定义为：

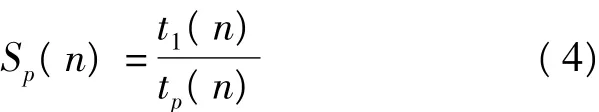
式中，t1(n)为求解一规模为n的问题的最优串行算法在单处理器上的运行时间，tp(n)为求解该问题的并行算法在p个处理器上的运行时间。最优的串行算法很难找到，甚至不存在，一般利用实际所用的串行算法来代替。

并行算法的效率定义为：

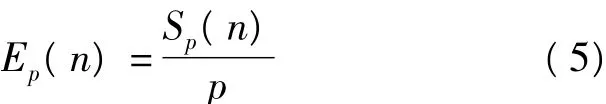
式中，p为并行算法运行所需的处理器数。

如果并行算法的加速比与处理器个数成正比，则称该并行算法具有线性加速比;如果Ep(n)＞1，则称之为超线性加速比。

3 数值分析

3.1 计算效率评测

由于利用重力梯度数据求解地球重力场是一个超大型的最小二乘问题。这对计算机硬件的要求较高。表1列出了30天，5 s采样的重力梯度观测数据在不同阶数下所对应的计算机资源需求。

从表1可以看出，对于普通的小型服务器(本文计算均基于小型服务器P575-2进行，具体参数见表2)而言，设计矩阵的存储基本上是不可能的，只能通过分块策略组成法方程。相对而言，预条件矩阵为一稀疏阵，采用CSR格式存储可以大大节省内存空间。下面对 Cholesky分解法、PCCG方法和OpenMP并行解法的法方程求解时间进行比较(不包括法方程的组成时间)，如表3所示。并行解法所采用的CPU数为8个。对于Cholesky分解法，由于计算时间过于冗长，仅计算至120阶。

表3显示，对于大数据量的计算，3种方法中PCCG方法的计算时间最短，恢复200阶的地球重力场仅需要24次迭代，耗时半个小时左右即可完成。比较两种严密求解方法，并行算法大大提高了求解的效率，这对于求解超大型的线性估计问题是非常好的一个选择。图2给出了并行解法加速比与CPU个数和模型阶数的关系。其中，左图的求解规模为120阶地球重力位模型，右图的CPU数固定为8个。图3则显示了相应的并行算法效率值。

从图3可以发现，设计的OpenMP并行解法具有超线性加速比。随着CPU个数的增加，并行算法的效率值逐渐降低，但这种现象是建立在降低总解算时间的基础之上。此外，随着求解规模的增加，并行算法的效率值逐渐增加，充分说明了OpenMP并行解法对于求解超大型线性问题的高效性。

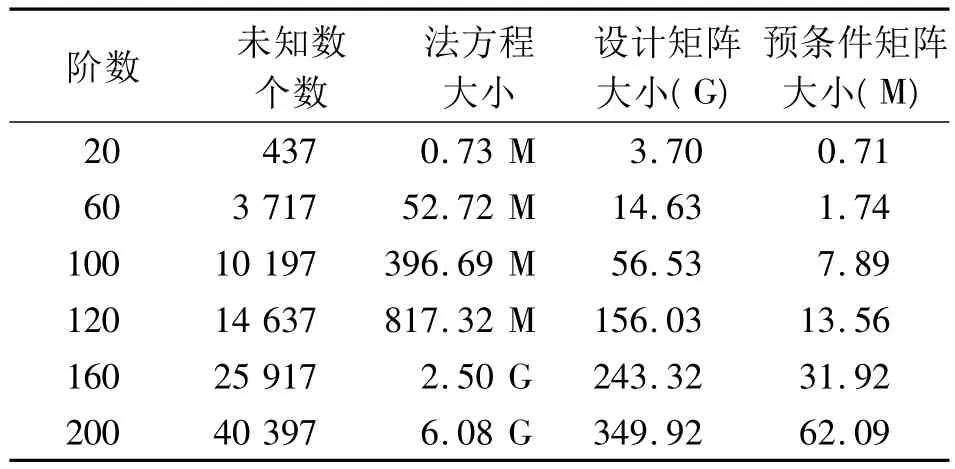
表1 不同阶数对应的计算机硬件资源需求Tab.1 Computer hardware resource dependence of different degree

表2 IBM P575-2服务器主要参数Tab.2 Main parameters of IBM P575-2 server

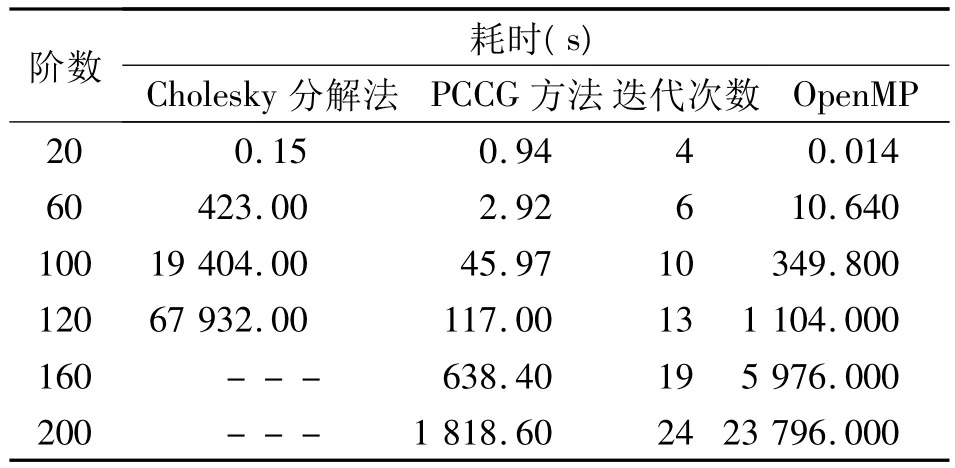
表3 不同数值解法的法方程求解时间比较Tab.3 Comparison among the computation time for normal equation solution with different numerical methods

3.2 PCCG方法与并行解法的精度比较

PCCG方法经过24次迭代计算即可达到收敛，其求解效率较之Cholesky分解法和OpenMP并行解法都要高，对于超大型线性问题尤为显著。梯度模拟数据利用EIGEN-GL04C地球重力位模型计算获得，阶数计算至200阶，然后基于空域最小二乘法［3-5］，分别利用预条件共轭梯度方法和OpenMP并行解法恢复地球重力场，阶数同样取至200阶。结果见图4～7。

从图4可以看出，除低次项以外，PCCG方法能够以10-16以上的精度恢复地球重力场，而并行算法则较之更高。相对而言，低次项的精度较低，这主要是由极空白问题引起的。对比两种方法的模型阶误差(图5)可以看出，并行算法精度较之PCCG方法要高一个数量级左右，达到10-14以上，但PCCG方法收敛较为迅速，且精度能够满足求解的需要。对比两极大地水准面以及大地水准面误差纬向变化图(图6，7)可以发现，PCCG方法获取的大地水准面在极区引入了一定的误差，最大在1 mm左右，随着纬度的升高，其精度愈来愈低，但是其引入的误差对全球重力场的解算可以忽略不计;并行算法则不同，除两极地区外，其他区域的精度分布较为均匀，除了计算机舍入误差外，OpenMP并行解法计算严密，未引入其他误差。

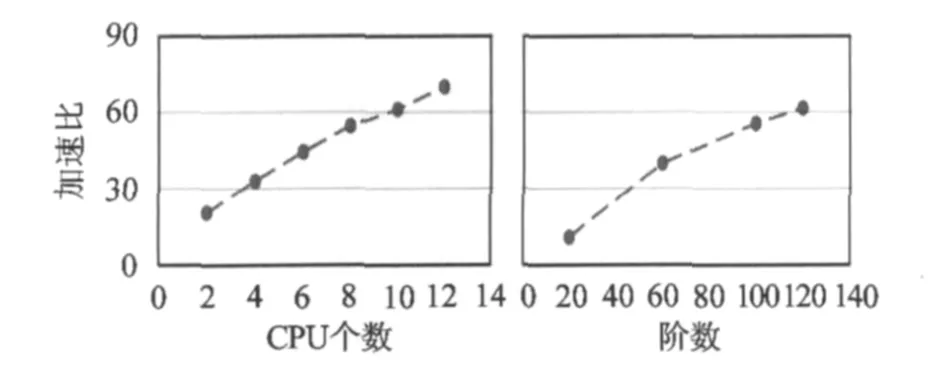
图2 OpenMP并行解法加速比与CPU数和阶数的关系Fig.2 Relation between OpenMP parallel algorithm speedup and CPU number as well as number of degree

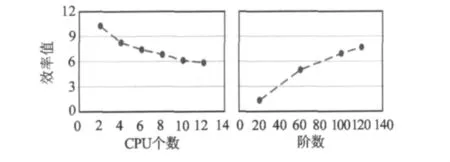
图3 OpenMP并行解法效率值与CPU数和阶数的关系Fig.3 Relation between OpenMP parallel algorithm efficiency and CPU number as well as number of degree

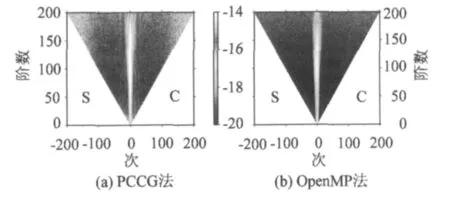
图4 PCCG方法与OpenMP并行解法的球谐系数误差谱Fig.4 Error spectrum of spherical harmonic coefficients of PCCG method and OpenMP parallel algorithm

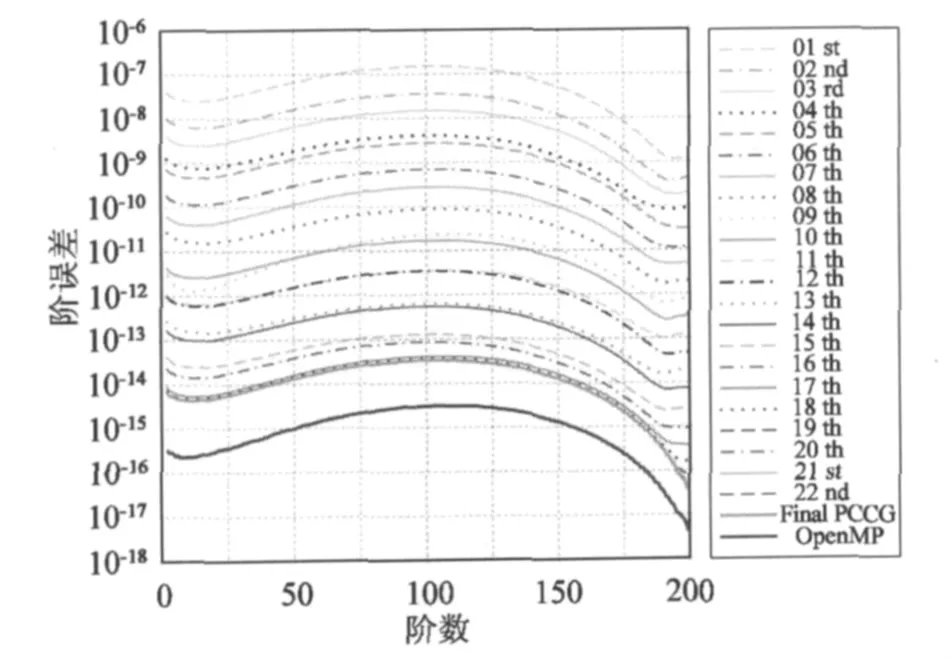
图5 PCCG方法与并行算法的模型阶误差比较Fig.5 Comparison between model’s degree error RMS of PCCG method and OpenMP parallel algorithm

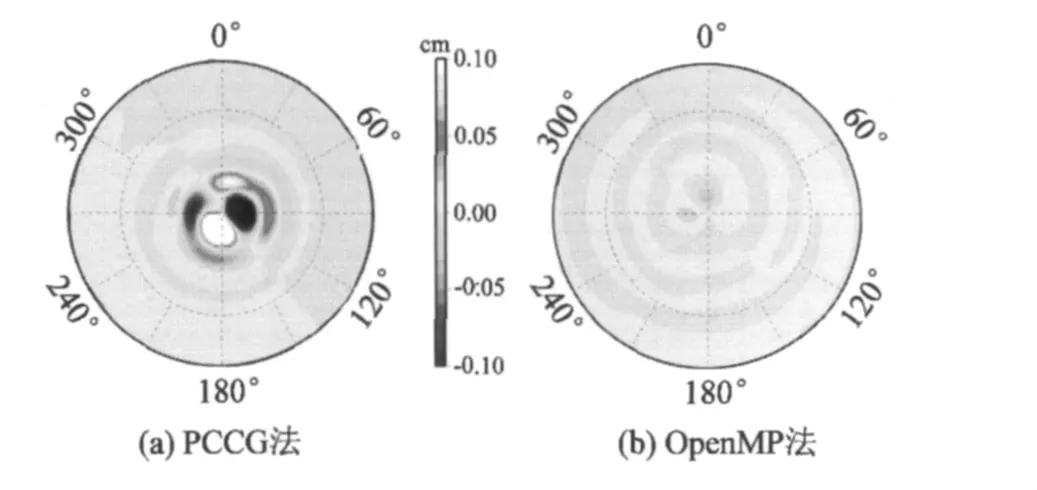
图6 PCCG方法与OpenMP并行解法的大地水准面误差极区分布Fig.6 Distribution of geoid error RMS in the polar area of PCCG method and OpenMP parallel algorithm

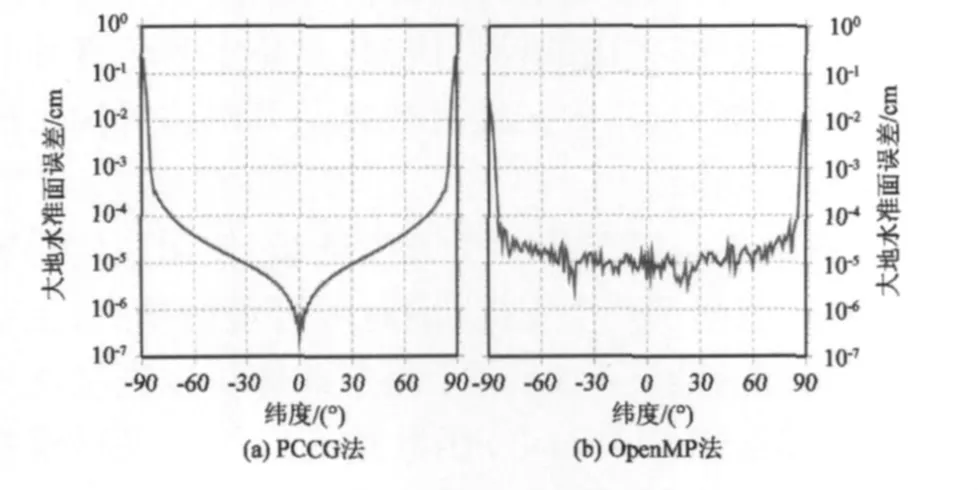
图7 PCCG方法与OpenMP并行解法的大地水准面误差纬向分布Fig.7 Latitudinal dependence of geoid error RMS of PCCG method and OpenMP parallel algorithm

3 结语

卫星重力梯度数据确定地球重力位模型最终可化为一大型最小二乘求解问题。针对GOCE卫星重力梯度观测数据的海量特征，对地球重力位模型的数值解法，包括Cholesky分解法、预条件共轭梯度法以及OpenMP并行解法3种方法，进行了系统研究和详细分析。研究表明，预条件共轭梯度方法能够在满足求解精度的要求下，有效地提高大型矩阵求逆的效率，但这也带来了一定精度的损失;OpenMP并行算法具有简单通用、移植性和可扩展性好、开发快速的特点，能够在不损失求解精度的条件下，有效提高计算效率。特别是在计算机硬件条件有限的情况下，OpenMP并行解法无疑是一个非常好的选择。

1 Rummel R，et al.Spherical harmonic analysis of satellite gradiometry［R］.Delft：Netherland Geodetic Commission， 1993.

2 Koop R.Global gravity field modeling using satellite gravity gradiometry［R］.Delft：Netherland Geodetic Commission，1993.

3 徐新禹.卫星重力梯度及卫星跟踪卫星数据确定地球重力场的研究［D］.武汉大学，2008.(Xu Xinyu.Study of determining the Earth’s gravity field model from satellite gravity gradient and satellite-to-satellite tracking data［D］.Wuhan University，2008)

4 钟波.基于GOCE卫星重力测量技术确定地球重力场的研究［D］.武汉大学，2010.(Zhong Bo.Study on the determination of the Earth’s gravity field from satellite gravimetry mission GOCE［D］.Wuhan University，2010)

5 朱广彬.卫星重力梯度测量技术确定地球重力场的理论方法研究［D］.武汉大学，2010.(Zhu Guangbin.Research on the theory and methodology for the Earth’s gravity field determination using satellite gravity gradiometry measurement［D］.Wuhan University，2010)

6 徐士良.FORTRAN常用算法程序集［M］.北京：清华大学出版社，1992.(Xu Shiliang.Fortran algorithms commonly used procedures set［M］.Beijing：Tsinghua University Press，1992)

7 Ditmar P and Klees K.A method to compute the Earth’s gravity field from SGG/SST data to be acquired by the GOCE satellite［M］.Delft University Press，2002.

8 郑锋，李名世，蔡佳佳.基于OpenMP的并行遗传算法探讨［J］.心智与计算，2007，1(4)：396-402.(Zheng Feng，Li Mingshi and Cai Jiajia.Parallel genetic algorithms based on OpenMP［J］.Mind and Computation，2007，1 (4)：396-402)

9 李晓梅，吴建平.数值并行算法与软件［M］.北京：科学出版社，2007.(Li Xiaomei and Wu Jianping.Numerical parallel algorithms and software［M］.Beijing：Science Press，2007)

ON NUMERICAL METHODS FOR DETERMINATION OF EARTH GRAVITY FIELD MODEL USING MASS SATELLITE GRAVITY GRADIOMETRY DATA

Zhu Guangbin1)，Chang Xiaotao1)，Zou Xiancai2)，Xu Xinyu2)and Wang Jianqiang3)

(1)Satellite Surveying and Mapping Application Center，SBSM，Bejing 100830
2)School of Geodesy and Geomatics，Wuhan University，Wuhan 430079
3)Institute of Surveying and Mapping，East China Institute of Technology，Fuzhou344000)

On the basis of Space-Wise Least Square method，three numerical methods including Cholesky decomposition，Pre-conditioned conjugate gradient and Open Multi-Processing parallel algorithm are applied into the determination of gravity field with satellite gravity gradiometry data.The results show that，Cholesky decomposition method has been unable to meet the requirements of computation efficiency when the computer hardware is limited.Pre-conditioned conjugate gradient method can improve the computation efficiency of huge matrix inversion，but it also brings a certain loss of accuracy.The application of Open Multi-Processing parallel algorithm could achieve a good compromise between accuracy and computation efficiency.

satellite gravity gradiometry;Cholesky decomposition;pre-conditioned conjugate gradient;open multiprocessing parallel algorithm;data processing

1671-5942(2011)06-0140-05

2011-03-19

国家自然科学基金(40874012，40904003，40974016，41004007)

朱广彬，男，1981年生，博士，主要从事卫星大地测量学的研究.E-mail：whu_gbzhu@hotmail.com

P223

A