基于土地利用分类模型和重力模型耦合的人口分布模拟——以武汉市人口数据为例*

丁文秀 赵 伟 左德霖 张亦梅 王维维 杨志强

(1)湖北省地震局，武汉 430071 2)中国地震局地震研究所，武汉430071)

基于土地利用分类模型和重力模型耦合的人口分布模拟
——以武汉市人口数据为例*

丁文秀1，2)赵 伟1，2)左德霖1，2)张亦梅1，2)王维维1，2)杨志强1，2)

(1)湖北省地震局，武汉 430071 2)中国地震局地震研究所，武汉430071)

将土地分类模型和重力模型耦合形成新模型，并以武汉市人口数据为例，用耦合后的新模型模生成武汉市人口网格数据。经数据验证表明，耦合后的新模型在计算精度方面有了较大的提高。

土地分类模型;重力模型;模型耦合;网格;人口分布;

1 引言

人口分布一直是地理学家、社会学家研究的热点，同时也是国家、社会重点关注的问题。特别是当重大突发性自然灾害发生后，政府需要对灾情快速评估并开展有效的应急救援工作，这时如何在第一时间获取受灾人口的数量及分布就显得尤其重要。目前公开的人口数据的最小统计单元是街道办、乡、镇;再加上全国人口普查每十年一次，时间跨度太长，以街道办、乡、镇为单元的人口统计数据已远远满足不了灾情评估的需求。

因此利用多源数据将人口数据从行政区单元细化到千米网格单元(1 km×1 km)，提高人口数据的空间分布精度，已成为国内外研究的热点课题。美国、日本、英国等国家［1，2］都在研究人口数据千米网格化的方法，并将网格化数据用于灾害评估中，取得了很好效果。国内研究人员也对人口千米网格做了大量研究，文献［3-5］通过土地利用分类模型生成了全国公里网格人口数据库，文献［6-9］通过重力模型生成了全国公里网格人口数据库。

然而，通过土地利用分类模式或者重力模型生成得到的网格人口数据，都存在着较大误差。为进一步提高人口网格数据的精度，本文以武汉市人口数据为例，分析了土地利用分类模型、重力模型生成的人口网格数据存在较大误差的原因;并将上述两种模型耦合后模拟出武汉市的人口网格数据，精度得到明显提高。

2 模型对比分析

2.1 土地利用分类模型

通过土地利用分类模型生成人口网格数据，是建立在人口密度与土地利用类型对应关系基础之上的。认为每种土地利用类型对应不同的人口密度，即赋予不同的人口密度权值，并综合考虑了水文、气候、地形地貌等影响因子之后计算得到(表1)，其计算公式为［5］：

其中，Areak为网格内第k种土地面积，Dk为第k种土地对应的平均人口密度。

以武汉市人口数据为例，利用上述方法生成人口千米网格数据，其平均误差是15.7%。经分析认为误差存在的原因主要为：该模型认为同一种土地类型上的人口数据是均匀分布的，不符合城市内人口分布的空间特征;没有考虑社会历史因素、交通网等因素对人口分布的影响。

2.2 重力模型

通过重力模型生成人口网格数据，是建立在人口密度与植被净生产力(NPP)、数字高程(DEM)、城市的规模、交通设施等因素之间的对应关系基础之上的。认为距离城区越近、交通设施越密集、植被净生产力(NPP)越小，人口密度越大。因此在综合考虑各项因子对人口分布的影响之后，得到每个网格的人口分布权重，进行一步计算每个网格的人口数据(表1)，其计算公式为［6-9］：

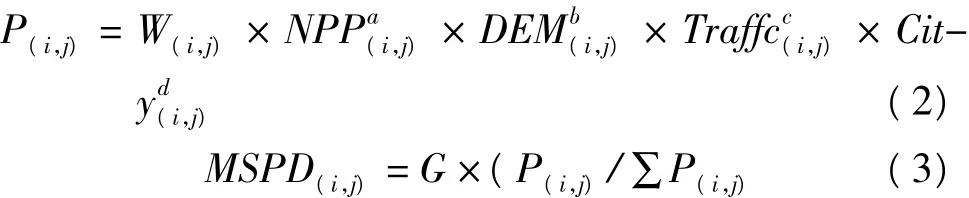
其中，P(i，j)为网格的人口分布权重，W(i，j)为网格内的水域面积，为网格的植被净第一生产力归一化指数，Traffi为交通因子归一化指数，DE为数字高程归一化指数，Ci为中心城区影响归一化指数，MSPD(i，j)为网格的人口，G为行政区域的总人口，∑P(i，j)为行政区域内所有网格的总人口分布权重。

同样以武汉市人口数据为例，利用上述方法生成人口网格数据，其平均误差是18.6%。分析认为误差产生的主要原因有：武汉市高程值变化不大，多为平原地区，高程的影响很小;在城乡结合处有着较大的交通影响因子和城市影响因子，而这些地区人口分布相对较少(或没有人)，误差很大。

表1 土地利用分类模型、重力模型的建模因子Tab.1 The factors of land use classification model and gravity model

2.3 土地利用分类模型和重力模型的耦合

鉴于分别利用上述两种模型生成千米网格人口数据存在较大误差，本文尝试将土地利用分类模型和重力模型耦合，在综合考虑两个模型的建模因子的情况下，生成了精度更高的人口数据网格模型。考虑的建模因子详情见表2，其计算公式如下：

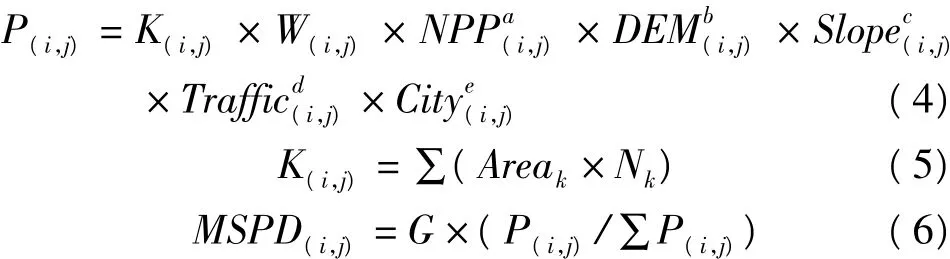
其中，Slope(i，j)为网格的坡度值，K(i，j)为网格内各种土地利用类型的综合权重值，Areak为网格内第k种土地的面积，Nk为第k种土地的权重值。

3 模型实现

根据武汉市人口数据，融合土地利用分类模型和重力模型的优点，生成的人口网格数据如图1所示。建模及计算大致分为以下几个步骤：

1)逐一将建模因子的属性数据进行网格化(1 km×1 km)，并存入数据库;

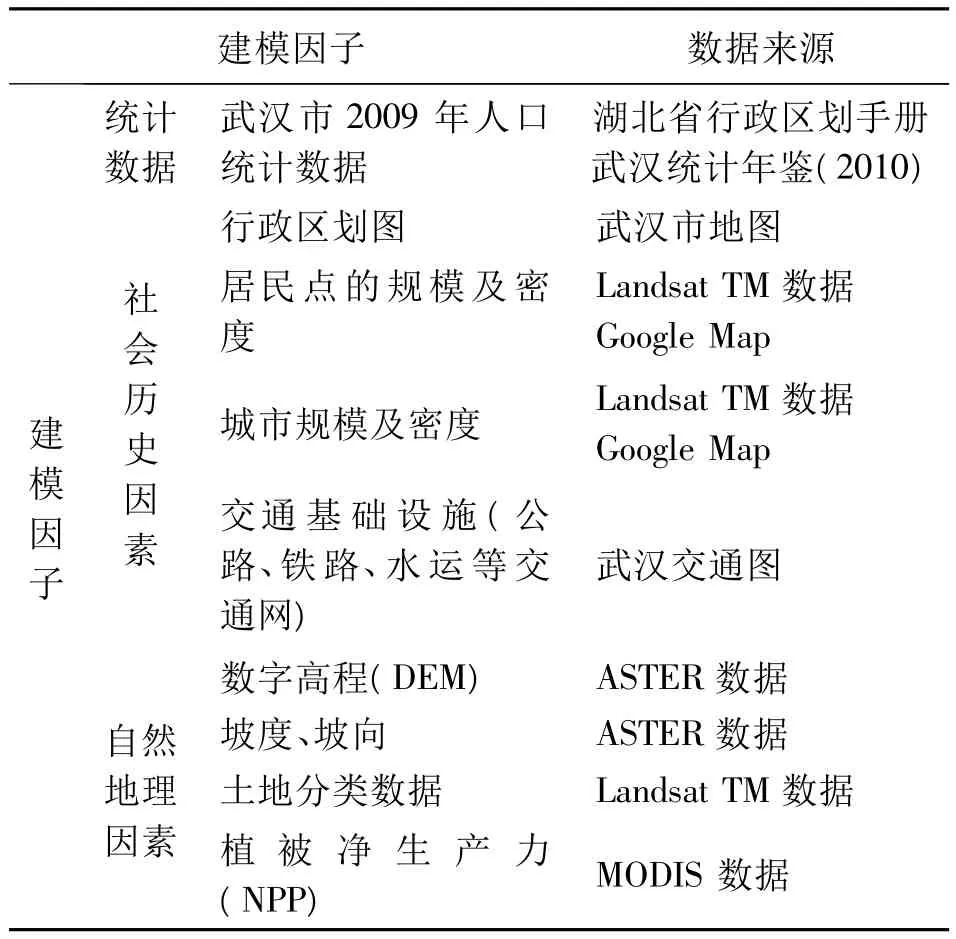
表2 本文模型的建模因子和数据来源Tab.2 The factors and the data sources for this paper

2)实现网格内建模因子属性数据的归一化处理;

3)通过公式(4)计算每个网格的人口分布权重值;

4)通过公式(6)计算每个网格的人口。

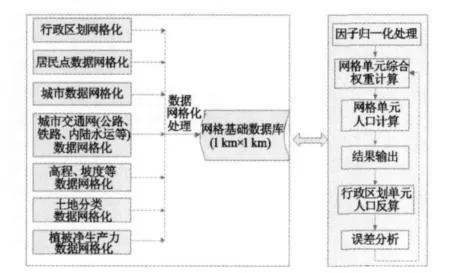
图1 人口数据网格化流程图Fig.1 Flowchart for producing gridded population data

3.1 建模因子归一化计算

1)以行政区划图为基础生成1 km ×1 km的千米网格。

2)土地利用分类数据归一化

首先利用landsat TM数据1～7波段中地物(水系、建设用地、林地、农田等)的光谱特征，反演出武汉市土地利用分类数据，接着将土地分类数据网格化，最后根据公式(5)生成归一化因子K(i，j)。

3)交通网因子归一化计算

对武汉市自然村、居民点和交通图分析，发现绝大部分的自然村、居民点分布在交通网1千米缓冲区范围内。因此先将铁路网、公路网、内陆水运网等交通网数据网格化，接着将3种交通网长度之和保存在每个网格中，最后除以每个网格的最大值，得到0至1之间的交通网因子归一化数据。计算公式为：

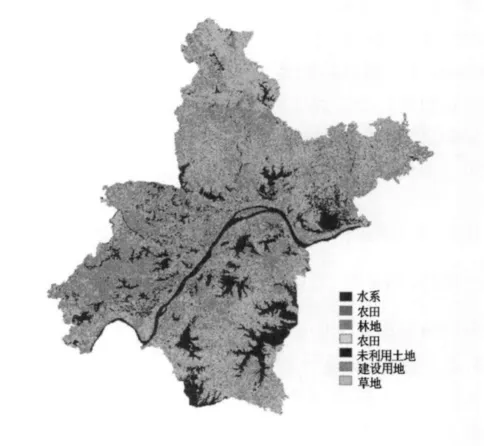
图2 武汉市土地利用分类数据Fig.2 Land use classification data of Wuhan

式中，railway(i，j)、road(i，j)、waterway(i，j)分别是铁路网、公路网、内陆水运网数据网格化后的数值，Traffic(i，j)是归一化后的交通网的综合影响因子。

4)植被净生产力(NPP)归一化计算

先对武汉市陆地植被净第一生产力(NPP)统计分析，计算出人口稠密区的NPP的平均值为276.8 gcm-2a-1，然后利用公式(8)，得到0至1之间NPP归一化数据。

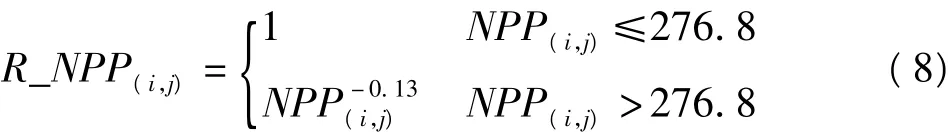
5)数字高程(DEM)、坡度(slope)归一化计算

通过分析发现，市居民点分布主要集中在海拔200 m以内、坡度10°以内的地区。利用公式(9，10)，得到0至1之间的高程和坡度归一化数据。

6)中心城区影响因子归一化

重力模型认为城市和人口聚集区对周边的人口分布有吸引力，对于人口的吸引力大小与该城镇的规模成正比，与到该城镇的距离成反比。先用land-sat TM遥感数据反演出武汉市土地利用类型，识别出城市与城镇的分布范围及规模，接着通过和GoogleMap提供的影像对比，确定城市内部主城区的面积及其中心点坐标，最后利用公式(11)，得到0至1之间的中心城区影响因子归一化数据。

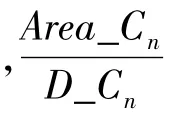
3.2 综合权重计算

将各建模因子代入公式(4)，计算出每个网格的人口分布综合影响权重值，其计算结果如图3所示。

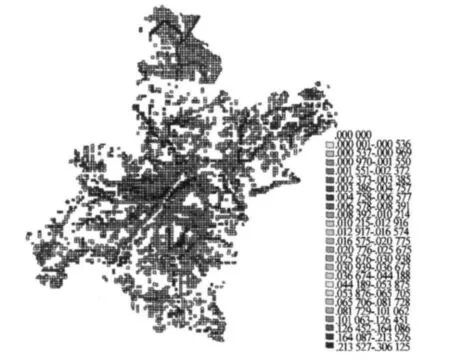
图3 武汉市人口权重分布Fig.3 Gridded weight data of Wuhan

3.3 人口计算

将武汉市总人口和各网格权重值代入式(6)，计算出每个网格的人口数据，其计算结果如图4。

4 误差分析

为验证用本文方法实现的武汉市人口网格数据的准确性，从千米网格数据库中反算出武汉市每个街道办、乡、镇的人口数据，并与统计数据对比分析。结果表明数据的平均误差为10%(表3)。由此可见用土地利用分类模型和重力模型耦合后生成的人口公里网格数据，其精度要高于单用一种模型得到的数据。

5 结论

图4 武汉市人口分布Fig.4 Gridded population data of Wuhan

表3 模拟计算结果Tab.3 Results from the simulation

利用重力模型体现了城市内部中心人口分布衰减性的特点，另一方面用土地利用分类模型控制人口的分布区域，经数据精度验证，结合两种模型优点计算人口网格数据的方法可有效地提高人口网格化模型的计算精度。

1 Marja Tammilehto-Luode and Lars Backer.Grid data and area delimitation by definition towards a better European territorial statistical system［J］.Statistical journal of the United Nations ECE，2000，(17)：109-117.

2 张超，万庆，张继权.基于格网数据的洪水灾害风险评估方法—以日本新川洪灾为例［J］.地球信息科学，2003，(4)：69-72.

3 Yang Xiaohuan and Ma Hanqing.Natural environment suitability of China and its relationship with population distributions［J］.Environmental Research and Public Health.2009，6：3 025-3 039.

4 Yang Xiaohuan，et al.An updating system for the Gridded population database of China based on remote sensing，GIS and spatial database technologies［J］.Sensors，2009，9：1 128-1 140.

5 江东，杨小唤，王乃斌，刘红辉.基于RS、GIS的人口空间分布研究［J］.地球科学进展，2002，17(5)：734-738.

6 Yue Tianxiang，et al.Numeriacl simulation of population distribution in China［J］.Population and Enviroment，2003，25 (2)：141-163.

7 Tian Xiangyue，et al.Suface modeling of human population distribution in China［J］.Ecological Modelling，2005，181，461-478.

8 刘纪远，等.中国人口密度数字模拟［J］.地理学报，2003，58(1)：17-23.

9 王英安.中国人口密度模拟误差分析及其软件系统研究［D］.山东师范大学，2003.

SIMULATION OF POPULATION DISTRIBUTION COUPLED WITH LAND USE CLASSIFICATION MODEL AND GRAVITY MODEL——TAKING WUHAN CITY AS AN EXAMPLE

Ding Wenxiu1，2)，Zhao Wei1，2)，Zuo Delin1，2)，Zhang Yimei1，2)，Wang Weiwei1，2)and Yang Zhiqiang1，2)

(1)Earthquake Administration of Hubei Province，Wuhan 430071 2)Institute of Seismology，CEA，Wuhan430071）

It is a hot spots of the study of population distribution used by grid cells.The advantages and disadvantages of the land use classification model and the gravity model are compared and analysed，then these two models with Wuhan population data are coupled.The results indicate that the new coupled model improves computing accuracy effectively.

land use classiffication model;gravity model;model coupling;grid;distribution of population

1671-5942(2011)Supp.-0127-05

2011-01-16

国家软科学研究计划(2010GXS5B156);中国地震局地震应急青年课题(CEA_EDEM-201010);中国地震局地震研究所所长基金(IS201056070)

丁文秀，男，1981年生，研习员，主要从事地震应急工作.E-mail：dwx_cug@126.com

O212

A