零次差分CHAMP卫星简动力定轨和SLR轨道验证*

柴 强 乔学军 闵 轩

(1)中国地震局地震研究所，武汉 430071 2)武汉大学灾害监测与防治研究中心，武汉430079)

零次差分CHAMP卫星简动力定轨和SLR轨道验证*

柴 强1)乔学军1)闵 轩2)

(1)中国地震局地震研究所，武汉 430071 2)武汉大学灾害监测与防治研究中心，武汉430079)

采用零次差分简化动力法对CHAMP卫星GPS相位观测资料进行精密轨道计算，并将计算结果与CHAMP快速轨道进行比对。结果表明X、Y、Z方向差值均方根为0.061 m、0.060 m与0.066 m，精度达到了厘米级;同时利用全球人卫激光观测数据对所求轨道进行验证，表明其精度优于20 cm。

人卫激光测距;零次差分简化动力法;CHAMP卫星;精密定轨;快速轨道

1 基于零次差分简化动力法CHAMP卫星定轨

人造卫星在绕地球运行时受到的力可大致分为中心力及非中心力，非中心力又称为摄动力，摄动力主要包括：地球非球体引力摄动，多体摄动，固体潮摄动，海潮摄动，大气阻力摄动，太阳辐射压，地球辐射压摄动，及因相对论效应引起的摄动［1］。包含各

种摄动力影响的卫星运动方程式为［2-8］：

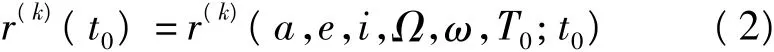
式中，K=0，1，参数a、e、i、Ω、ω、T0代表时刻的6个轨道元素，q1，…，qd代表未知的扰动力参数。

简化动力法求解轨道充分利用卫星的动力学模型和几何观测数据等信息，通过卫星经验加速度的随机过程噪声(一般看作为一阶高斯-马尔科夫过程模型)，在动力学模型和几何观测信息间进行最优加权，并利用过程噪声参数吸收动力学模型误差，获得卫星轨道的最优估计［9］。通过调整动力学模型噪声和相关时间参数，在动力学模型和观测数据信息之间进行平衡。当相关时间τ→∞和动力学模型噪声σ→0时，简化动力法定轨转化为动力法定轨;当τ→0，σ→∞，简化动力法定轨转化为纯几何法定轨［10］。

在实际计算中，采用零次差分，将轨道元素，动力参数与其他相关参数(接收机钟差改正，相位整周模糊度等)同时求解。虚拟随机参数则是在径向，沿轨道方向，横向3个方向上，依经验每6分钟给予一组解，可使得后处理轨道的均方根达到最小化［11，12］。

2 观测数据

在零次差定轨中，高精度的GPS星历与高采样率GPS时钟差起着关键性的作用，目前只有CODE提供2004年4月以后的的高采样率时钟差，同时为了防止由于采用不同机构发布的产品带来的模型误差［13］，计算统一采用CODE发布的精密星历和高采样率时钟差。

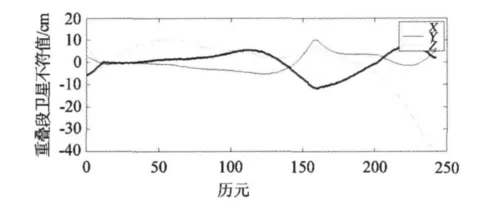
图1 RSO轨道重叠段位置差Fig.1 Location difference at overlap orbits of RSO

本文采用2004年年纪日102—121共20天的CHAMP卫星星载GPS数据，为了评估计算精度，将计算的结果与参考轨道进行对比，其中CHAMP用于对比的轨道为GFZ发布的快速轨道RSO(http：// www-app2.gfz-potsdam.de/pb1/op/champ/)。GFZ数据中心提供的单天RSO轨道包括两个数据文件，每个文件包含14个小时CHAMP卫星轨道数据，采样率为30 s。有两个小时的轨道重叠，由于在轨道解算开始和结束阶段的约束比较弱，由此造成轨道重叠精度较低。图 1给出了 103天的重叠段(22：00—24：00)卫星轨道不符值，由图1可以看出，位置差值大部分在-10 cm至10 cm之间，但Z方向的末端差值达到近40cm，显然这部分数据的精度较差，但同时为了保证数据的连续性，在数据拼接过程中将14个小时的数据首尾各去掉一个小时，这样既可以在一定程度上削弱轨道重叠精度低带来的影响，又可将文件拼接成连续轨道。

3 观测模型动力模型

精密定轨采用无电离层非差线性组合观测值L3。表1给出了具体的观测模型和动力模型。

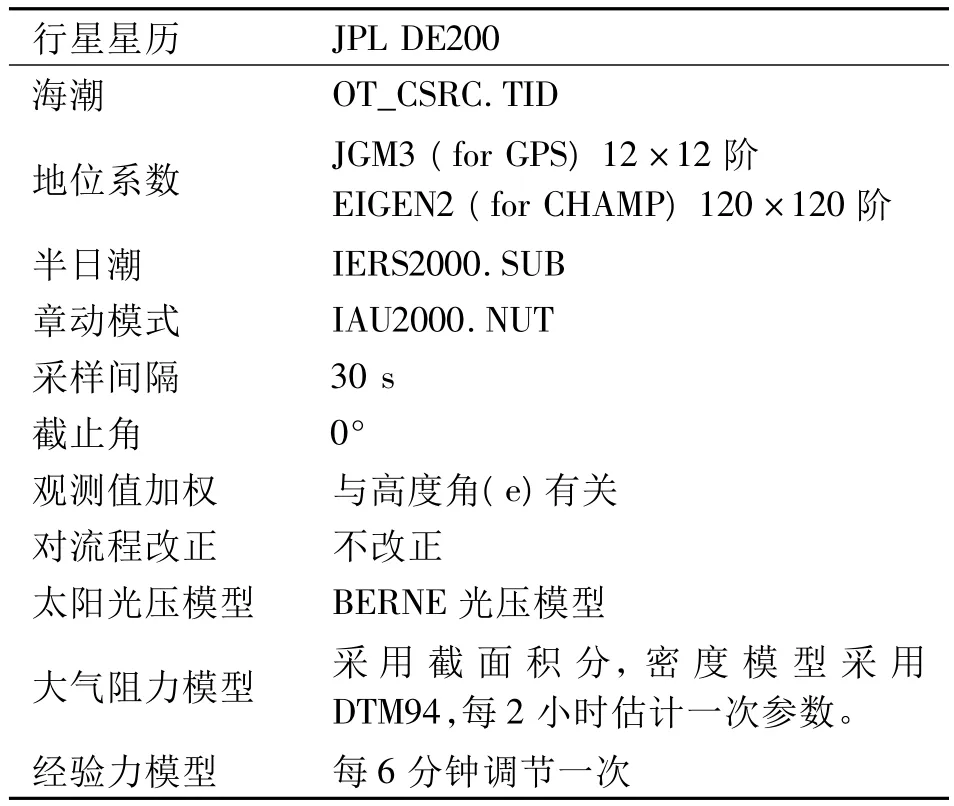
表1 观测模型和动力模型Tab.1 Observation model and force model

4 精密定轨结果及分析

将求解轨道与GFZ发布的快速轨道进行比较，结果以X、Y、Z 3个方向表示。图2给出了计算简动力轨道与RSO在X、Y、Z 3个方向的差异。3方向差异最大值分别为0.318 m、0.488 m和0.642 m。图2显示在每天的起止时刻的差值较大，这主要是由于在轨道的边界处约束较差，产生边界效应，其他时刻则主要由于该时刻观测数量较少，导致平差求解后无法获得较好的成果。

图2 简动力轨道与CHAMP RSO 3方向差值Fig.2 Differences in X，Y，Z directions between the reduced-dynamic orbits and the GFZ rapid science orbits

图3为本文的定轨结果与RSO比较的差值的均方差，3个方向20天平均均方差值分别为0.061 m、0.060m和0.066m。由此结果来看，即使有数据差异值较大，所解算20天轨道的精度仍可达到厘米级。

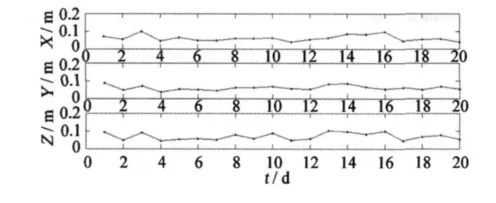
图3 定轨结果与RSO比较的差值均方差Fig.3 RMS difference in X，Y，Z directions between the reduced-dynamic orbits and the GFZ rapid science orbits

5 SLR轨道验证

5.1 观测数据

为了与CHAMP定轨相对应，直接采用2004年年纪日102—121共20天的SLR标准点数据，由于CHAMP卫星轨道高度低，飞行速度快，难以追踪，在计算时间段内共有14个SLR观测站2 302个标准点数据。计算中剔除了残差大于60 cm的标准点数据(假设本文计算的精密轨道精度为20 cm，按照3倍中误差进行剔除)，其中测站 7501(Hartebeesthoek，S.Africa)由于数据残差较大被全部剔除，测站7810(Zimmerwald Switzerland)的激光测距仪测得的激光脉冲的频率(L2)与其他测站频率(L1)不同被剔除，同时取10°截止高度角，最后得到1 869个标准点数据。

5.2 计算与分析

在计算的各种误差中，数值误差较小，可以忽略不计;通过迭代可以削弱线性化带来的误差;观测模型误差中，最不容易精确化的是大气折射改正，本文采用Marini-Murray公式改正。

CHAMP的精密星历是在TT时间系统下以30 s为间隔给出的，而SLR观测资料采用的时间系统是UTC时间系统，因此，在检核计算时，首先要统一两者的时间系统。本文采用10阶拉格朗日内插公式将CHAMP卫星内插到SLR观测时刻，通过比较SLR直接测得的站星距与CHAMP卫星反算的站星距，得到CHAMP卫星的轨道检核结果。图4给出了测得的各个测站的站星距与轨道反算的站星距之间的差值结果。图5显示了SLR残差值的均方根，20天RMS的平均值为14.4 cm。

6 结论与讨论

1)动力学法定轨使随机误差的作用减至最少，但力模型误差的影响较大。几何法定轨虽然消除了力学模型的影响，但随机误差大。简动力法充分吸收了几何定轨法和动力学定轨法的优点，通过对过程噪声的选择，一方面降低了动力学定轨法对力学模型的过度依赖，另一方面又确保了轨道的连续性和轨道外推的精度。简动力法定轨的困难在于如何选择适当的过程噪声［14］。本文使用简动力法对CHAMP卫星进行定轨，解算的轨道和RSO的差值大部分都在0.1 m以内，精度达到厘米级。

图4 SLR残差Fig.4 SLR residuals for orbit solutions

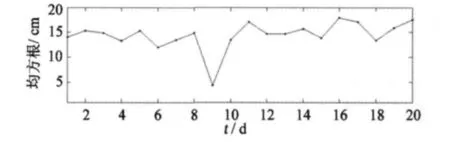
图5 反算的站星距和SLR直接测得的站星距差值的均方根Fig.5 RMS difference between SLR measurement and orbit solutions

2)在利用SLR观测数据检测CHAMP卫星轨道时，每天均方根误差均小于20 cm，其中20天的平均RMS为14.424 cm，而采用零次差分简动力法得到的CHAMP轨道与GFZ发布的快速轨道的3方向的差值均方根分别为0.061 m、0.060 m与0.066 m。SLR精度较差的原因主要有：在对SLR数据进行预处理时，未完全剔除系统误差较大的台站观测数据;GFZ提供的快速科学轨道本身的精度问题。

3)由于GFZ发布的快速轨道精度一般，而SLR观测资料的精度已经达到亚厘米级，在扣除系统偏差的影响后，SLR测得的站星距与轨道反算的站星距之间的误差，主要是由轨道反算的站星距的误差引起的，而在轨道反算的站星距误差中，轨道误差又是主要的误差源。

4)利用SLR资料检核卫星轨道的结果仅能代表卫星轨道在某一分量上的精度，即只能检核CHAMP卫星星历误差所引起的用户等效距离误差，而不能给出精密星历在各个方向的精度。

5)由于GFZ未发布CHAMP卫星2004年年纪日102—121天的最终精密轨道，所以本文采用快速轨道作为参考轨道，同时采用各种方法保证快速轨道的准确性。

1 秦显平，焦文海.利用SLR检核CHAMP卫星轨道［J］.武汉大学学报(信息科学版)，2005，30：38-41.

2 刘红新.CHAMP卫星定轨方法研究［D］.同济大学土木工程学院，2006.

3 吴江飞.星载GPS卫星定轨中若干问题的研究［D］.中国科学院上海天文台，2006.

4 Steigenberger P and Rothacher M.Quality of reprocessed GPS satellite orbits［J］.Journal of Geodesy，2008，83：241 -248.

5 Jaggi A and Hugentober U.Pseudo-stochastic orbit modeling techniques for low-Earth orbiters［J］.Journal of Geodesy，2006，80：47-60.

6 Thaller D and Mareyen M.Preparing the bernese GPS software for the analysis of SLR observations to geodetic satellite［A］.Proceedings of the 16th International Workshop on Laser Ranging［C］.Poland，2007.

7 Carlos Javier Rodriguez Solano.Impact of albedo modelling on GPS orbits［D］.Technische University Munchen，2009.

8 Bock H and Huentobler U.Efficient precise orbit determination of LEO satellites using GPS［R］.Presented at COSPAR 2000，Warsaw，Poland，2000.

9 Koenig R and Reigber C.Satellite dynamics of the CHAMP and GRACE leos as revealed from space-and groundbased tracking［J］.Advances in Space Research，2003，31 (8)：1 869-1 874.

10 Yunck T P.GPS precise tracking of TOPEX/POSEIDON：Result and implication［J］.Journal of Geophysical Research，99(C12)：24 449-24 464.

11 Yunck T P and Wu S C.Precise tracking of remote sensing satellites with the globe positioning system［J］.IEEE Transactions on Geosciense and Remote Sensing，1990，28 (1)：108-116.

12 Lee-Lueng Fu，Edward J and Charles A Y.Topex/Poseidon mission overview［J］.Journal of Geophysical Research，1994，99(C12)：24 369-24 381.

13 Bisnath S B and Langley R B.Precise orbit determination of low earth orbiters with GPS point positioning［A］.Proceedings of Institute of navigation Technical Meeting 2001［C］.Long Beach，California.

14 Amiri-Simkooei A R and Tiberius C C J M.Assessment of noise in GPS coordinate time series：Methodology and results［J］.Journal of Geophysical Research，2006，112：1-19.

REDUCED-DYNAMIC ORBIT DETERMINATION OF CHAMP AND SLR VALIDATION

Chai Qiang1)，Qiao Xuejun1)and Min Xuan2)

(1)Institute of Seismology，CEA，Wuhan 430071 2)Hazard Monitoring and Prevention Research Center，Wuhan University，Wuhan430079)

From the CHAMP GPS phase data，Bernese5.0 is used with the zero-difference reduced-dynamic methods to compute CHAMP satellite orbits.The RMS difference in X，Y，Z directions between the reduced-dynamic orbits and the GFZ rapid science orbits are 0.061 m，0.060 m，0.066 m，respectively.In general，the accuracy of the computed orbits is at the centimeter level.On the basis of the SLR residuals analysis，which are computed as the differences between the SLR measurements minus the corresponding distances between the SLR station and the GPS-derived orbit positions，the accuracy of orbits is better than 20 centimeter level.

SLR;zero-difference reduced-dynamic methods;CHAMP satellite;precise determination;rapid satellite orbit

1671-5942(2011)Supp.-0081-04

2011-02-23

地震科技行业专项(200808080)

柴强，男，1986年生，硕士，研究方向为GNSS区域精密定轨.E-mail：chaiqiang18@163.com

P228.1

A