考虑二次压力梯度非线性渗流三区复合油藏模型分析

2011-11-10贾永禄张福祥杨向同秦世勇

东北石油大学学报 2011年5期

张林，贾永禄，张福祥，杨向同，秦世勇

( 1. 西南石油大学油气藏地质与开发国家重点实验室，四川成都 610500； 2. 中国石油塔里木油田分公司，新疆库尔勒 841000 )

渗流力学是开发地下流体资源的理论基础，近年来渗流理论不断完善，但有关非线性渗流问题的理论与应用研究处于初级阶段，非线性渗流力学的研究越来越受到重视，已成为现代渗流力学发展的新方向[1-3].由于二次压力梯度作用带来的理论误差达到20%以上[4]，在渗流研究中不应该被忽略.在流动方程中保留二次梯度项的非线性方法是由Odeh A S和Babu D K提出的[5].W W-G YEh针对非均质油藏建立考虑二次梯度非线性项的偏微分方程，运用隐式差分格式将控制方程离散化，得到数值解，并讨论各类参数对解的影响[6].Jan Finjord建立考虑二次压力梯度的渗流试井模型，通过分析强调二次梯度随时间变化后对井底流压的影响不可忽略的重要性[7-8].Chakrabarty C等研究含二次梯度影响的径向压力分布解析解，定量分析二次梯度项的影响[9].Streltsova T D进行非均质储层的试井研究，使用相似的技巧，从而避免求双孔隙度系统的联立解[10].Braeuning S等考虑井筒储集和表皮效应的非线性径向流动模型，分析二次压力梯度项在变流量试井分析中的影响[11].同登科等通过拉氏逆变换求得短时间和长时间的渐进解，讨论二次梯度对压力的影响，从而描述线性解和非线性解的差异[12-17].这些文献研究均质地层和双重介质油藏，笔者研究考虑二次梯度三区复合油藏模型，对样版曲线进行敏感性分析，发现二次压力梯度更能真实地反映复杂油藏的渗流规律.

1 非线性渗流方程

当单相流体通过多孔介质时，运用质量守恒原理得到直角坐标系下的流动连续方程：

(1)

式中:u为渗流速度；t为渗流时间；ρ为液体密度；φ为岩石孔隙度.

渗流运动方程符合达西定律，得到运动方程：

(2)

式中：k为油层渗透率；μ为黏度；p为压力.

多孔介质和液体是可压缩的，得到状态方程：

对弹性液体ρ=ρ0exp[Cρ(p-p0)],

(3)

对弹性多孔介质φ=φ0exp[Cr(p-p0)],

(4)

式(3-4)中:Cr为岩石等温压缩系数；Cρ为液体等温压缩系数；ρ0，φ0，p0为某一参考数值，通常取标准状况下的.

联立式(1-4)推出：

(5)

式中:Ct为综合压缩系数，Ct=Cρ+Cr.

将式(5)变换为径向圆柱坐标下：

(6)

式(6)为具有二次压力梯度项的非线性渗流控制偏微分方程，将压力梯度的平方项称为二次压力梯度项(Quadratic Pressure Gradient Term).传统渗流模型研究是通过假设小的压缩系数和压力梯度而将非线性项忽略，因此线性渗流是非线性渗流的近似、简化与处理，非线性渗流更符合原油在多孔介质中渗流的实际.

2 模型求解

2.1 物理模型

图1 三区复合油藏物理模型

假设：(1)圆形均质等厚油藏中心一口井定产量生产；(2)产层厚度全部打开，流体径向流入井内；(3)储层孔隙介质及渗透率呈三区分布特性，每区内均匀分布，各向同性，与压力无关(见图1)；(4)流体和岩石微可压缩，其压缩系数为常数，流体黏度为常数；(5)考虑井筒储集效应和表皮效应的影响；(6)忽略重力和毛管力影响；(7)等温达西渗流；(8) 外边界条件可以是无穷大地层.

2.2 数学模型

其中：下标1代表一区；下标2代表二区；下标3代表三区；r为离井的距离；rw为井半径；pi为原始地层压力；pw为井底压力；h为油层厚度；q为地面产量；Cs为井储系数；B为体积系数；Re为外边界距离；t为生产时间；p1，p2，p3为1区、2区、3区地层压力；r1，r2，r3为1区、2区、3区半径；k1，k2，k3为1区、2区、3区油层渗透率；φ1，φ2，φ3为1区、2区、3区储层孔隙度.

渗流偏微分控制方程为

(7)

(8)

(9)

式中：TD=tD/CD.

(1)初始条件：

p1D|TD=0=p2D|TD=0=p3D|TD=0=0.

(10)

(2)内边界条件：

(11)

(3) 连接条件：

对于压力连续，p1D|r=r1D=p2D|r=r1D,

(12)

p2D|r=r2D=p3D|r=r2D.

(13)

(14)

(15)

(4)外边界条件：

(16)

2)求解.

作变量代换

(17)

对式(7～16)进行变量代换后，模型变化为

(18)

(1)初始条件：

x1|TD=0=x2|TD=0=x3|TD=0=0.

(19)

(2)内边界条件：

(20)

(3)连接条件：

对于压力连续，x1D|rD=r1D=x2D|rD=r1D,

(21)

x2D|rD=r2D=x3D|rD=r2D.

(22)

(23)

(24)

(4)外边界条件：

(25)

引入基于TD的Laplace变换：

(26)

式中：z为拉氏变量.

对式(18～25)进行Laplace变换得其通解：

(27)

式中：I0(·)为第一类零阶变形贝塞尔函数；K0(·)为第二类零阶变形贝塞尔函数；I1(·)为第一类一阶变形贝塞尔函数；K1(·)为第二类一阶变形贝塞尔函数.

在井底处rD=1，当p=pw时，pD=pwD，将通解代入内、外边界条件和连续条件，可以得到在井底处关于xw的一组拉氏空间线性方程组：

(28)

式中：A,B,C,D,E,F为待定系数.

3 渗流规律

3.1 样板曲线

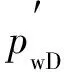
3.2 敏感性分析

受二次压力梯度影响的三区复合油藏井底压力动态响应特征曲线见图2.无穷大边界条件下的三区复合油藏压力和压力导数双对数非线性渗流特征曲线见图2(a).由图2(a)可以看出，三区复合油藏样版曲线的导数曲线出现不同台阶，由于压力波传到外区时间较长，外区物性差，使得二次梯度的影响强烈.当无因次二次压力梯度因数β为0时，则蜕化为线性模型，可以划分6个渗流阶段.

第Ⅰ阶段：为纯井筒储集阶段，油井开井生产，井筒中的积液流动，地层中原油处于静止状态，压力与压力导数双对数曲线呈单位斜率，线性模型与非线性模型相同，即非线性渗流是原油在地下多孔介质中的流动.

图2 三区复合油藏非线性渗流特征曲线

第Ⅱ段：为表皮效应反映阶段，油井近井地带存在污染(钻、完井等施工作业过程中可能造成地层堵塞)，压力导数曲线呈明显的“驼峰”状，线性模型与非线性模型之间开始出现差异，参数团(CDe2S)对渗流特征曲线的影响见图2(b).由图2(b)可以看出，参数团(CDe2S)的值越大，“驼峰”越明显.

第Ⅲ段：为1区渗流阶段，反映1区的地层特性，当1区达平面径向流阶段时，由于受到非线性作用，与线性模型相比，压力导数曲线不再遵循“0.5线”规则，而是位于“0.5线”下方.

第Ⅳ阶段：为2区渗流阶段，反映2区的地层特性，与1区相比，压力导数变换1个台阶，若2区物性(渗透率、孔隙度和岩石压缩系数等)比1区物性差，则压力导数曲线的台阶上升；若2区物性比1区物性好，则压力导数曲线的台阶下降；若2区与1区的物性差异越大，台阶上升(或下降)越明显(图2(c))；若1区半径越大，则压力波传到2区的时间越长，台阶出现的时间越晚(图2(d)).

第Ⅴ阶段：为3区渗流阶段，类似于第Ⅳ阶段，若3区物性比2区物性差，则压力导数曲线的台阶上升；若3区物性比2区物性好，则压力导数曲线的台阶下降；若3区与2区的物性差异越大，台阶上升(或下降)越明显(图2(c))；若2区半径越大，则压力波传到3区的时间越长，台阶出现的时间越晚(图2(d)).

第Ⅵ阶段：为外边界反应阶段，外边界距离越远，上翘或下掉的时间越晚.

3.3 非线性项影响

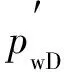
由表1和表2可以看出：储层物性越差，二次梯度的作用越明显；随着生产时间的增加，二次梯度的作用越明显；在同一量纲一时刻下，随着β的增大，线性与非线性量纲一压力之间的误差随之增大.当β较大时，二次梯度项影响不应被忽略.相反，如果β较小时，二次梯度项的影响较小，可以忽略不计.当β趋近于0时，样版曲线与常规模型样版曲线重合，即蜕变为常规模型.因此，非线性渗流规律更能代表原油在油藏中的真实流动规律，应加强非线性渗流理论研究.