燃气管道泄漏模型的研究进展

冯云飞，吴 明，闫明龙，陈 杨

（1. 辽宁石油化工大学 石油天然气学院，辽宁 抚顺 113001； 2. 中国煤炭科工集团重庆设计研究院，重庆 400010）

综合评述

燃气管道泄漏模型的研究进展

冯云飞1，吴 明1，闫明龙1，陈 杨2

（1. 辽宁石油化工大学 石油天然气学院，辽宁 抚顺 113001； 2. 中国煤炭科工集团重庆设计研究院，重庆 400010）

泄漏速率是燃气管道扩散模拟和风险评价的重要因素，同时也是管道泄漏检测不可缺少的一环。通过对国内外泄漏速率计算模型的应用分析，探讨了燃气管线泄漏率计算的主要模型和分类方法，罗列了稳态模型下小孔模型、大孔模型和管道模型的计算式，并指出其适用范围。对于大孔模型，提出了高压和低压分开计算泄漏率的方式。对比一些非稳态泄漏模型指出了较为合适的方程。

燃气管道；泄漏率；稳态模型；非稳态模型；大孔模型

天然气的易燃易爆性，使得其在管道输运过程中的泄漏危险性增加，轻者污染环境，重者带来火灾、爆炸甚至人身的伤亡，因此，有必要对燃气泄漏事故后果进行预测和风险评价。

泄漏速率的计算是天然气扩散数值模拟和风险评价的基础，针对其计算方法，国内外学者做出了不同的研究，大致可以分为稳态和非稳态两种模型[1~4]，前者是基于管线的应用,假设泄露过程管内各参数恒定，后者是根据输运的实际过程，各个参数随着输送时间而变化。严格意义上讲，一切管线的泄漏都是非稳态模型[5]，因为泄漏过程中管线内的压力、流速、温度以及气体密度等都会变化，然而由于泄露率的动态计算十分复杂，在计算过程中为了方便而进行简化，所以稳态和非稳态模型常常结合应用，以发挥两者的优势并弥补其不足。

1 泄漏模型

图1给出了管道泄漏的示意图，在距离管线起点eL处出现泄漏孔，1点为输气起始中心点，2点为泄漏孔处管道内中心点，3点为泄漏点。各参数分别用ip、ir、iT表示， 代表1、2、3点参数角标，eL为当量长度。

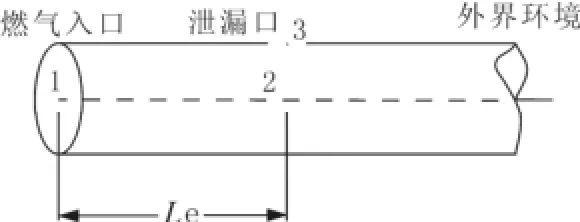
图1 天然气泄漏示意图Fig.1 The sketch of gas leakage

1.1 稳态模型

稳态模型按泄漏孔径(d)与管道直径(D)之比分为三个泄漏阶段，时为小孔模型、为孔口模型、为管道模型[1]。其中，小孔模型与管道模型较为简单，大孔模型的计算研究较为复杂并且相对较少。

1.1.1 小孔模型[1，4]

小孔模型的孔径管径比(Dd/)较小，可以认为管道内部参数不受泄漏过程的影响，气体泄漏为等熵膨胀过程，泄漏速率恒定为起始最大泄漏速率，考虑到输气管道在高压低温下运行，真实气体和理想气体之间的差别，在理想气体状态方程中引入压缩因子，以修复由于天然气可压缩性带来的误差，气体状态方程[6]：

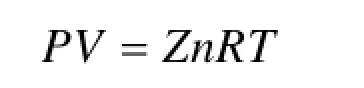
其中：P—管线压力；

V—气体体积；

n—气体的摩尔数；

R—气体常数；

T—气体温度；

Z—压缩因子。

由于管道运行一般压力较高，管道泄漏起始阶段，泄漏孔处环境压力与管内压力之比小于临界压比，其中，临界压比是临界压力和滞止压力的比值，

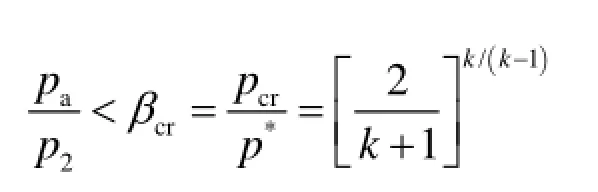
泄漏孔气体为临界流动状态。随着泄漏过程的进行，管道内压力减小，环境压力接近直至大于管内压力后，泄漏孔气体转变为亚临界流动状态。

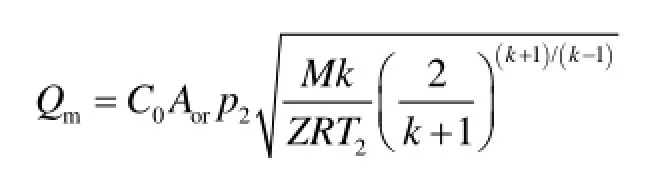
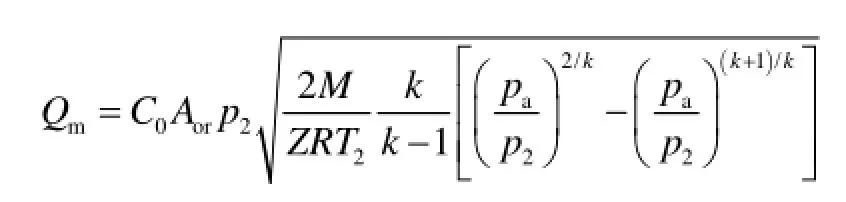
式中：Qm—气体泄露速率， kg/s；

C0—流量系数，当孔口为雷诺数Re＞30 000的非临界流动时，取为0.61，其他情况下取为1；

Aor—孔口截面积，m2；

Pa —大气压力，Pa；

k—比热容；

R—气体常数，取为8.314 J/（mol·K）；

M—气体摩尔质量。

1.1.2 大孔泄漏

当泄漏一定的时间，孔径增大，小孔模型不再适合，大孔泄漏有三种可能的状态：管内亚临界流，孔口临界流；管内亚临界流，孔口亚临界流；管内临界流，孔口临界流。Helena Montiel[7]根据此假设，分别推导出了三种泄漏状态下的计算方程，经过实验研究国内学者对此进行了修正和完善，董玉华等人[8]认为管内临界流动，孔口临界流这种状态不可能存在；而王兆芹等人[9]认为高压下会有管内亚临界孔口临界和管内孔口都是临界流动状态；低压时管道内为亚临界流动，孔口可以分别为临界和亚临界流动。

实际上，管道的低压和高压泄漏状况会有各方面的不同，各参数值也会有差别，在高压条件下管道发生泄漏会有：

(1)管内亚临界，孔口临界流动。满足如下关系：

泄漏过程中1、2、3各点参数之间的关系1、2点之间满足下式：

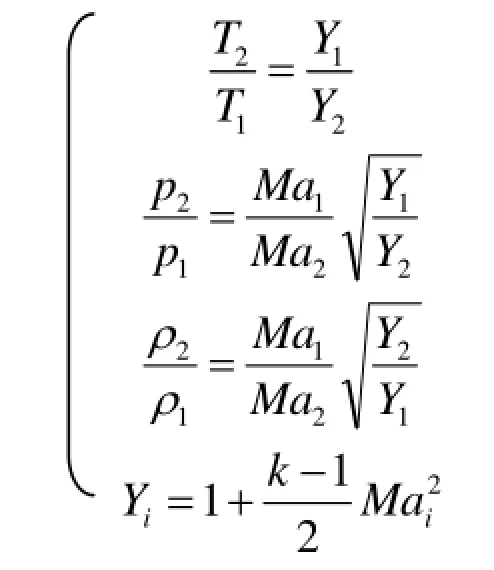
2、3点之间参数关系如下：

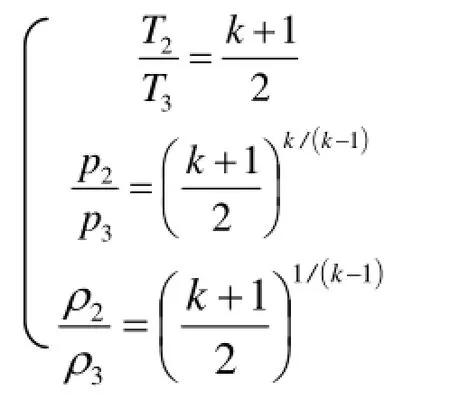
并且有：

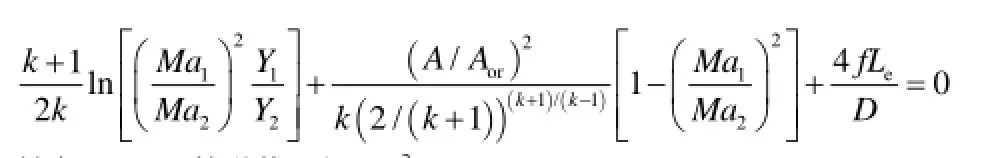
其中：A—管道截面积，m2；

f—范宁系数；

Le —管道当量长度，km。

(2)管内孔口均为临界流时：

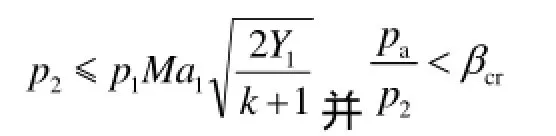
泄漏速率为：

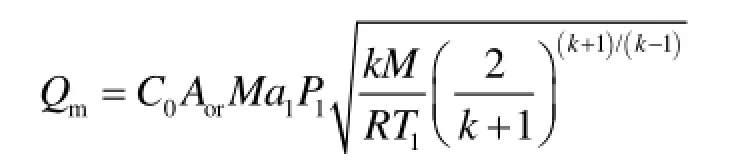
图1所示管道2、3点之间参数关系满足(5)式。并有：

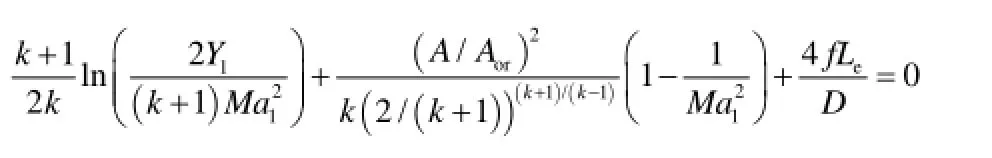
低压下管内为亚临界流动，初始泄漏孔为临界流，随着泄漏的进行，孔口变为临界流，由于低压下管内动量变化较小，管内亚临界流动过渡不到临界流动，仍然保持亚临界流动。当管内亚临界流动孔口临界流动时，此状态下泄漏速率计算式与高压状态计算式相同即式，当孔口流动减小到亚临界流动时有以下关系式：

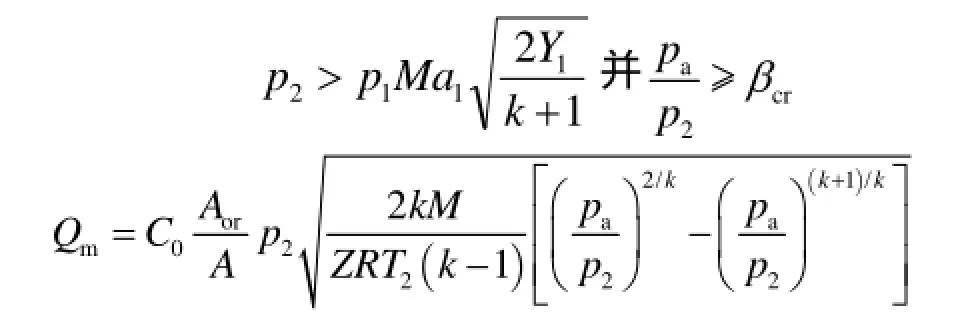
图1所示点1、2之间仍然满足(4)式，2、3点参数之间的关系：

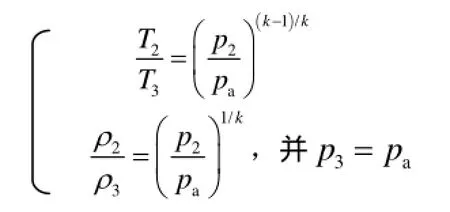
1.1.3 管道模型[6，10]

管道模型是管道的全截面断裂，此时图1中，管道中心点2处于外界环境，和泄漏孔中心点3处各个参数相同，泄漏过程已经不是等熵流动，Octave Levenspiel[11]根据稳态下的机械能和总能量守恒定律，对此模型的计算式进行了推导，如下：

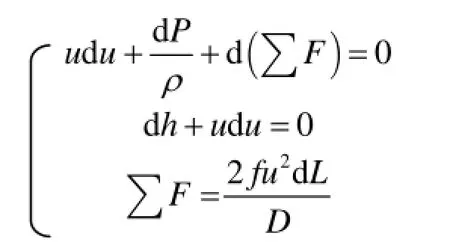
其中：u—气体流动速度，m/s；

ρ—气体的密度，kg/m3；

ΣF—单位质量的合力；

h为比焓，J/kg；

D—管道直径，m。

由上式得到：

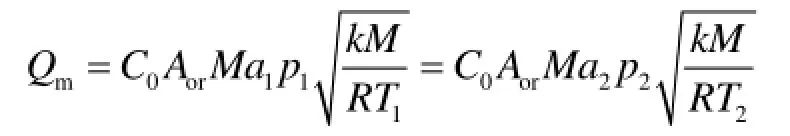
图1中1、2点参数之间的关系满足(4)式。同时有：

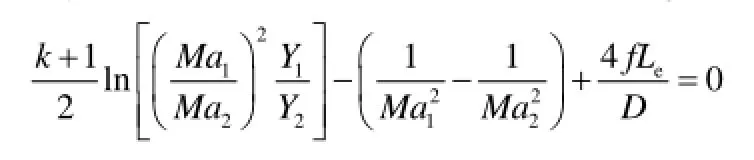
1.2 非稳态泄露模型：

在管道泄漏发生时，我们所遇到的泄漏情况大都非稳态模型，当泄漏孔较小时，气体的泄露过程对管内气体的各参数影响不大，可以认为是稳态泄漏，然而，随着泄漏孔不断增大，稳态模型势必有很大的误差，就不得不考虑非稳态状况了。针对此模型多数学者用微元分析法进行计算[7,8]，

即有：

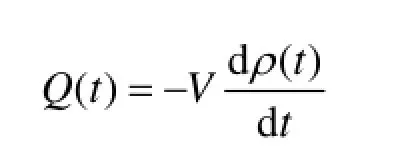
结合其他各方程可已分别得到孔口临界流动和亚临界流动的计算式。刘忠良等人[5]利用开口系统能量平衡方程，结合状态方程、连续性方程等得到了非稳态下孔口泄漏的计算式。实际上，管线一旦发生泄漏情况，相应的阀门会很快关闭，阀门关闭后，由于管内压力下降，孔口泄漏流动会由临界流转向亚临界流，当 时孔口为临界流动，管内压力逐渐降低，当 时，孔口变为亚临界流动。孔口流动由临界状态转变为亚临界状态的时间为临界泄露时间：

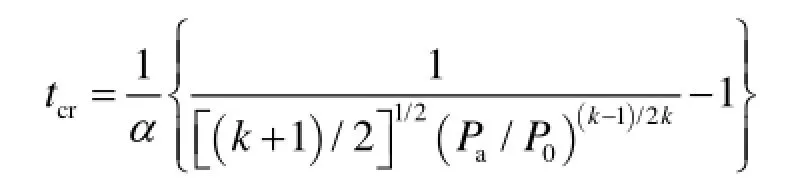
孔口为临界泄漏状态时将(1)式代入(14)式中，并结合绝热方程、状态方程可以得到如下关系式[12]：

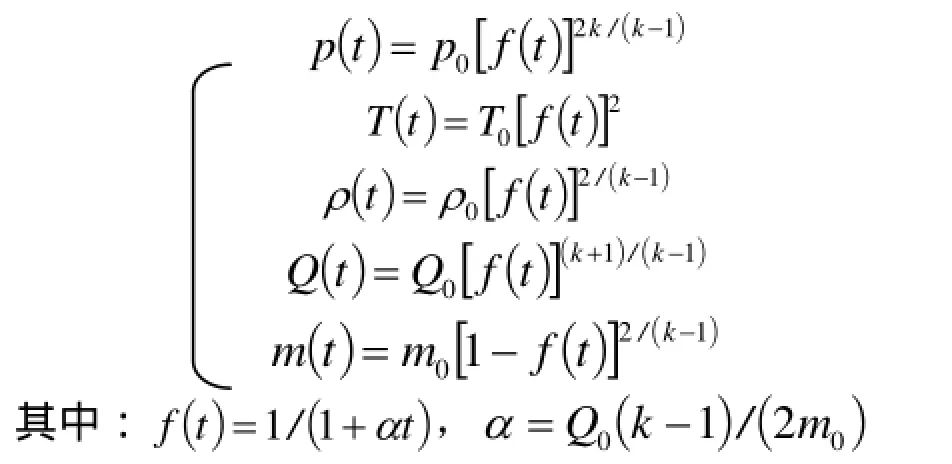
当孔口为亚临界流动时可将(2)式结合气体绝热方程、内能方程和状态方程等代入(14)式，可以得到如下亚临界状态下的计算式[5]：

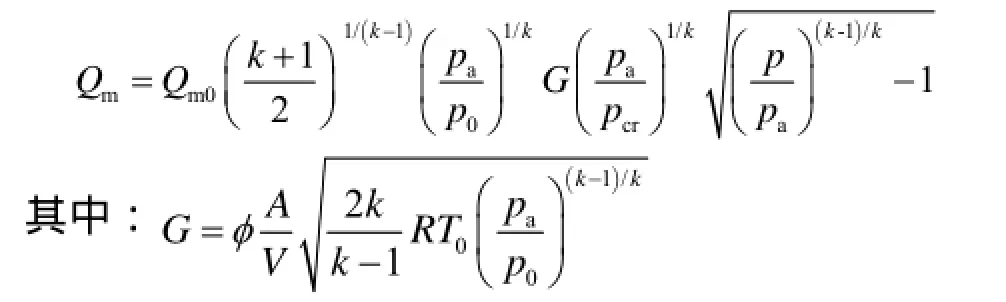
2 结束语

燃气管线泄漏率的计算中，以上模型都有不同的适用范围，可以按不同情况适当选择。对于泄漏孔较小时泄漏速率的计算，小孔模型即可以满足，当气体泄漏继续进行可以按高压低压管线选取特定的大孔泄漏模型。非稳态模型的研究较为鲜见，鉴于其在管线泄露检测和风险评估相应软件开发上的应用价值，以后应该是重点研究对象。同时，在实际计算过程中各种模型结合应用，以得到更精确的结果。

[1] 肖建兰，吕保和，王明贤,等.气体管道泄漏模型的研究进展[J].煤气与热力，2006，26(2):7-9.

[2] 崔斌，韦忠良.燃气管道非等温非稳态泄漏模型[J].油气储运，2010，29(1)：36-37，40.

[3] 于明，狄彦，帅建.输气管道泄漏率计算与扩散模拟方法述评[J].管道技术与设备.2007，15(4):16-18.

[4] 霍春勇，董玉华，余大涛,等.长输管线气体泄漏率的计算方法研究[J].石油学报.2004，25(1):101-105.

[5] 刘忠良，罗志云，王皆腾,等.天然气管道泄漏速率的确定[J].化工学报，2008，59(8):2121-2126.

[6] 沈维道，工程热力学[M]. 第三版.北京.高等教育出版社,2001

[7] Helena Montiel. Mathematical modeling of accidental gas release[J].Journal of Hazardous Materials，1998，59(2/3):211-233.

[8] 董玉华，周敬恩，高慧临,等.长输管道稳态气体泄漏率的计算[J].油气储运，2002，21(08):11-15.

[9] 王兆芹，冯文星，李在蓉,等.高压输气管道泄漏模型[J].油气储运，2009，28(12):28-30.

[10] 袁恩熙，工程流体力学[M].北京.石油工业出版社.2006.

[11] Octave Levenspiel.Engineering flow and heat exchange[M].New York:Plenum press，1986:39-55.

[12] woodward J L,mudan K S.Liquid and gas discharge rates through heles in process vessels[J].Loss Prev. in process.Ind.,1991,4(4):160-166.

Research Progress in Leakage Models for Gas Pipelines

FENG Yun-fei1，WU Ming1，YAN Ming-long1，CHENG Yang2
（1. College of Oil &Gas, Liaoning Shihua University, Liaoning Fushun 113001, China；2. China coal Technology&Engineering Group Chongqing Design&Research Institute ,Chongqing 400010, China）

The leakage rate is a crucial factor of gas pipeline discharging dispersion simulation and risk assessment, in addition, it's an indispensable part of gas pipe leakage detection, too. In this paper, according to application and analysis of domestic and foreign calculation models of leakage rate, main calculation models of gas pipe leakage rate were discussed as well as classification methods. Three steady calculation models including pinhole leakage model, larger hole leakage model and pipe fracture model were listed, and their application scopes were indicated. For the larger hole leakage model, the method of respectively calculating leakage rates based on high and low pressure was put forward. Compared with various kinds of calculations of leakage rate at the unsteady calculation models, more suitable equations were obtained.

Natural gas pipeline; Leakage rate; Steady leakage model; Unsteady leakage model; Larger hole leakage

TQ 018

A

1671-0460（2011）12-1255-04

辽宁省科学技术项目(编号：20022159)

2011-09-16

冯云飞（1983-），男，安徽阜阳人，辽宁石油化工大学在读研究生，研究方向：埋地管道泄漏事故有效性评价方法研究。E-mail：yunff@sohu.com。