Excel在《水力学》教学过程中的应用

2011-11-05杨艳

长江工程职业技术学院学报 2011年3期

杨艳

（长江工程职业技术学院，武汉 430212）

在水力学教学过程当中，常遇到试算和利用同一个公式需要代入不同数值进行反复计算的问题，如梯形断面渠道正常水深、临界水深计算和明渠恒定非均匀流水面曲线分析。若按照传统板书讲解例题，教师大多时间用在板书上，用手工计算不仅计算量大，而且计算精度低，以致学生在课堂上来不及解决疑问，耗时费力，教学较为被动。若是利用计算机语言编制程序来计算，需要具有一定的编程能力，对大多数学生有一定难度，不易掌握。若采用多媒体教学法，运用Excel软件强大的计算功能，可以有效节省课堂讲授时间，提高课堂效率，而且可以使同学们将已学过的计算机基础知识与工程实例结合起来，调动学生积极性和培养学生思考解决工程实例的兴趣。现以梯形断面渠道正常水深计算为例，介绍Excel计算的方法。

1 Excel计算梯形断面渠道正常水深h0

1.1 传统解法

由于正常水深是高次隐函数，不能直接求解，传统的解法有以下几种：

（1）用现成的图表图解法求解，这种方法比较麻烦且精度低，计算者也不可能随时都带着工具书；

（2）采用试算法借助辅助曲线求解，这种方法很麻烦且精度不高；

（3）利用计算机高级语言编写程序进行求解，但这要求计算者掌握至少一种算法语言，而所使用的计算机中又要具有相应的高级语言环境，具体应用起来比较困难。

1.2 Excel的数值计算方法

现在计算机的应用越来越普及，且绝大多数计算机用户都使用微软的Windows操作系统和Office软件，我们可以利用Office组件中Excel的强大计算功能，来实现水力学高次方程试算问题，它不需要计算者必须掌握计算机高级语言，也不需要计算机中具有计算者所使用的高级语言环境，只需要计算者将手工试算过程的计算公式填写在Excel的单元格中，利用Excel的“单变量求解”等强大的计算功能，就可以方便、快捷地解决问题。

“单变量求解”是一组命令的组成部分，这些命令有时也成为假设分析工具。如果已知单个公式的预期结果，而确定此公式结果的输入值未知，则可使用“单变量求解”功能反求输入值。使用“单变量求解”功能，通过单击“工具”菜单上的“单变量求解”即可。当进行单变量求解时，Excel会不断改变特定单元格中的值，知道依赖于此单元格的公式返回所需的结果为止。

1.3 计算实例

已知某梯形断面渠道（见图1），底宽b＝8m，边坡系数m＝2，底坡i＝0.0005，糙率n＝0.025，当渠道过流量 Q＝25m3／s时，试求渠道正常水深h0。

（1）计算公式

如图1所示梯形断面渠道，计算正常水深h0的公式为：

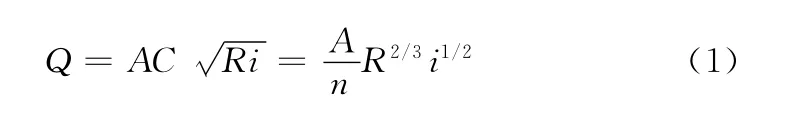
图1 渠道断面图

对于梯形断面明渠，上式可写成

式中：Q——渠道通过的流量（m3／s），为已知值；

A——渠道的过水断面面积（m2），A＝（b＋mh）h；

C——谢才系数（m1／2／s），用曼宁公式计算，C为渠道的糙率；

R——渠道的水力半径（m），为湿周，

m——渠道的边坡系数，m＝tgα；

i——渠道的底坡；

当Q、i、n、m、b已知时，式（2）为关于水深的一元高次方程，难以求解，可以使用Excel“单变量求解”功能解决。

（2）计算步骤。

①输入已知数据。将已知的Q、i、n、m、b填入相应的单元格中，如图2所示。

图2 计算正常水深h0已知数据填充图

②假设水深，计算过水断面上的水力参数A、X、R、C、Q。将过水断面上的水力要素符号h、A、X、R、C、Q按顺序填入同一行不同的单元格中，如图3所示。

图3 断面水力参数A、X、R、C、Q计算填充图

设任意一个初始水深h，例如h＝1m。将h值及表1中提供的计算A、X、R、C、Q的Excel计算公式依次输入A4、B4、C4、D4、E4、F4单元格中。每完成一个输入，按回车键即可完成一项计算。例如，计算过水断面面积A的方法为：单击B4单元格，使其成为活动单元格；在B4单元格中输入“＝（＄D＄1＋＄F＄1＊A4）＊A4”（输入位置在图中的第一行，f（x）＝…），按回车键即可计算出水深h＝1m的过水断面面积，A＝10m2。以此类推，可求出X、R、C、Q的数值，计算结果见图3。应当引起注意的是：在输入Excel计算公式时，前面必须输入“＝”号。

应当注意，在表1中所列的Excel计算公式中，已知的数据应引用绝对单元格，如例题中b、m、i、n；而欲求的正常水深以及随正常水深变化的量A、X、R、C、Q，在计算过程中是可变的，故应引用相对单元格。二者的区别在于，引用绝对单元格应在已知数据所在的单元格所处的列、行的序号前加“＄”，如渠道底宽b＝8m，“8”处在D列第一行，不管计算哪一个水力要素值，但凡遇到底宽b，均写为“＄D＄1”。而引用相对单元格则不需要加“＄”。如计算水利半径R，过水断面面积A、湿周X均随水深h而变化，故应引用相对单元格。A的数据和X的数据分别处在B列第四行和C列第四行，因此水力半径R的Excel计算公式应写在D列第四行，在此单元格输入“＝B4／C4”。

另外，表1中所列的Excel计算公式，是与断面水力参数填充的单元格位置相对应的，断面水力参数填充的位置一旦发生变化，相应的Excel计算公式也会随之变化。如图4所示，本例题变化已知数据n、i的输入位置，表1中所列的Excel计算公式也将改变，例如相应的水力半径R的Excel计算公式变为“＝B3／C3”输入到D3单元格中，流量Q的Excel计算公式变为“＝B3＊E3＊SQRT（D3＊＄J＄1）”输入到F3单元格中，见图4中的Excel公式编辑栏。

表1 正常水深h0的Excel计算公式

图4

③利用Excel“单变量求解”功能求解渠道正常水深h0。

由图3可知，当初始水深h＝1m时，计算得到的流量为7.719m3／s，显然和已知流量 Q＝25m3／s不符。改变水深，流量也会随之变化，当某一水深h刚好使流量Q＝25m3／s时，此水深h就是我们欲求的正常水深h0。利用Excel“单变量求解”功能，可以方便地解决这一问题，方法如下：

在图3中，单击F4单元格，使其成为活动单元格；在“工具”菜单上单击“单变量求解”，弹出如图5（a）所示的“单变量求解”对话框。

在单变量求解对话框的“目标单元格”中输入F4（流量所在单元格），“目标值”中输入25（已知流量），“可变单元格”中输入＄A＄4（欲求的渠道正常水深h0所在的单元格），结果如图5（b）。填写完毕后单击“确定”按钮，弹出如图6所示的“单变量求解状态”对话框。

单击“单变量求解状态”对话框的“确定”按钮后即可完成计算任务，如图7所示。由图7可以知道单变量求解后最终h0＝1.916m。计算成果保留的小数点位数可以人为设置，但是对计算精度没有任何影响。

图5 单变量求解对话框

图6 单变量求解成果图

图7 使用Excel计算正常水深成果图

正常水深初始值设置为多少，对最终计算成果影响极小。如果初始值设置准确，仅仅是提高计算机的计算速度。如果对计算精度要求更高的话，可以设置Excel的“迭代精度”。在“工具”菜单上，单击“选项”，再选择“重新计算”选项卡，可以设置“最多迭代次数”和“最大误差”值，如图8所示。Excel的默认值分别为100和0.001，一般使用Excel的默认值就可以满足计算要求。