长江三角洲地区深基坑降水与地面沉降模拟预测耦合模型研究
2011-11-04戴根宝
戴根宝,杨 民
(江苏省地质工程有限公司,江苏 南京 210018)
长江三角洲地区深基坑降水与地面沉降模拟预测耦合模型研究
戴根宝,杨 民
(江苏省地质工程有限公司,江苏 南京 210018)
长江三角洲地区深基坑降水复杂,且极易引起地面沉降地质灾害问题,传统的基于地下水动力学原理的解析解模型(Theis公式或Dupuit公式)已难以满足降水设计模拟计算的需要,尤其是无法预测降水引起的地面沉降问题,深基坑降水与地面沉降耦合模型将地下水渗流模型和土体应力-应变模型耦合起来,可根据基坑地下水位的控制要求,同时模拟计算出降水井的布局、各井的开采量和地面沉降量。据此确定出的基坑降水方案既能满足地下水位的控制要求,又能对降水引起的地面沉降进行最优化控制。
基坑降水;地面沉降;优化设计;长江三角洲
0 引言
长江三角洲分布有复杂、巨厚的第四纪松散沉积层,其间发育有多层厚度较大的孔隙承压含水层,各含水层之间又以弱透水的粘性土层相分隔,并发生强烈的水力联系,构成了一个复合含水层系统,具有较高的承压水位。深大基坑的开挖必须依靠大降深的减压降水保证基坑稳定与施工安全,但大降深的降水又使原有的水土应力平衡状态受到破坏,从而引发地面沉降等人为地质灾害,不仅给国民经济的发展带来了不可估量的损失,而且给人民的生命财产安全带来了严重威胁。如何正确地模拟、预测重大工程深基坑降水引起的地下水渗流场的变化及由此而引起的地面沉降,优化降水设计方案,有效地控制地下水位下降所引起的地面沉降,已成为一个亟需解决的重要课题。
长江三角洲是我国经济最为发达的地区,也是城市化程度最高的地区。近年来,随着国民经济的飞速发展,人口的不断增加,城市建设规模的不断扩大,地下空间的开发已日益得到重视,且不断向着大和深的方向发展,有的基坑底板已进入第Ⅰ承压含水层,承压含水层对基坑开挖施工的安全威胁越来越大,再加上工程场地施工条件的限制,承压水减压降水的难度也急剧增加。
总之,承压水降水的成功与否已成为地下工程建设中十分关键的一环,直接关系到工程的成败,亟需有一套完整、成熟的可用于长江三角洲基坑降水优化设计的模拟计算模型。该模型研究不仅具有重大的理论意义和实用价值,并且能产生良好的社会效益和经济效益,具有广阔的推广应用前景(张阿根等,2005)。
1 国内外研究现状及发展趋势
国内外基坑工程降水设计,通常根据降水试验及基于地下水动力学原理(薛禹群等,2000),采用解析解模型(Theis公式或Dupuit公式)进行。进入20世纪90年代,随着工程建设的不断发展,大型基坑的不断涌现,场地施工条件复杂化程度的不断提高(如深部含水层厚度大、降水井为非完整井、地下水渗流为三维非稳定流、基坑周围的不同支护结构等),上述方法的使用显得越来越力不从心,尤其是由基坑降水引起的土体变形更是无法预测。因此,到了20世纪90年代后期,人们试图用能够刻画基坑地质体、降水工程结构和施工过程的数值解法来设计基坑降水方案,并将地下水渗流模型和土体应力-应变模型耦合起来,力争在预测基坑降水引起地下水渗流场变化时,对降水引起的地面沉降进行同步预测,以实现对基坑降水引起的地面沉降进行最优化控制的目的。但迄今仍未形成一套完整、成熟、可直接用于指导基坑降水方案设计的模拟计算模型。
基坑降水渗流问题是具有自由面的非稳定渗流问题(毛昶熙,2003),属复杂的非线性问题,常用的数值解法是有限差分法和有限单元法,并采用迭代法来求解代数方程,其解的稳定性一直是模型求解的难点。国内外学者提出了许多求解方法,如Bathe提出的单元渗透矩阵调整法,马淑芝等提出的复合单元法,王贤能等提出的高斯点法,Desai提出的剩余流量法,张有天提出的初流量法,速宝玉提出的节点虚流量法等。此外,还有变分不等式法、截止负压法、丢单元法、子单元法和虚单元法等。付延玲等提出了改进的复合单元渗透矩阵调整法,将自由面单元分为干湿单元以及过渡单元,且采用罚函数法解决了在高斯点附近解易出现振荡、稳定性差的缺点。
基坑降水过程实际是渗流场和应力场相互影响、相互作用的过程。关于土体和流体相互作用的研究最早见于K Terzaghi对地面沉降的研究,提出了著名的有效应力原理,并建立了一维固结模型,之后Biot在此基础上取得了一些开创性的研究成果,建立了较为完善的三维固结理论(钱家欢等,1996),Verrujit进一步发展了多相饱和渗流与孔隙介质耦合作用的理论模型,在连续介质力学的系统框架内建立了Euler型多相流体运移和变形孔隙介质耦合问题的理论模型。基于上述基本理论,目前关于基坑降水过程提出了许多计算模型,主要有水土分算模型、部分耦合模型以及基于比奥固结理论的全耦合模型。全耦合模型由于可一次性同时求出渗流场和应力场,从而自然地考虑了渗流场与应力场之间的耦合效应。但目前大多数模型并未考虑土体的变形参数和渗透性质随土体中应力场改变的动态变化,实际上随着土体应力场的改变,土体的变形参数和孔隙率以及渗透性也必然发生改变,因此在预测由深基坑降水引起的地面沉降时,不仅要考虑土体变形参数随有效应力状态的变化,还要考虑渗透性的相应动态变化,这样可使模型更加贴近实际,进一步提高了计算的精度。
2 地下水渗流与地面沉降耦合模型
2.1 地下水三维渗流与太沙基一维固结地面沉降耦合模型
2.1.1 地下水运动数学模型(骆祖江等,2006)
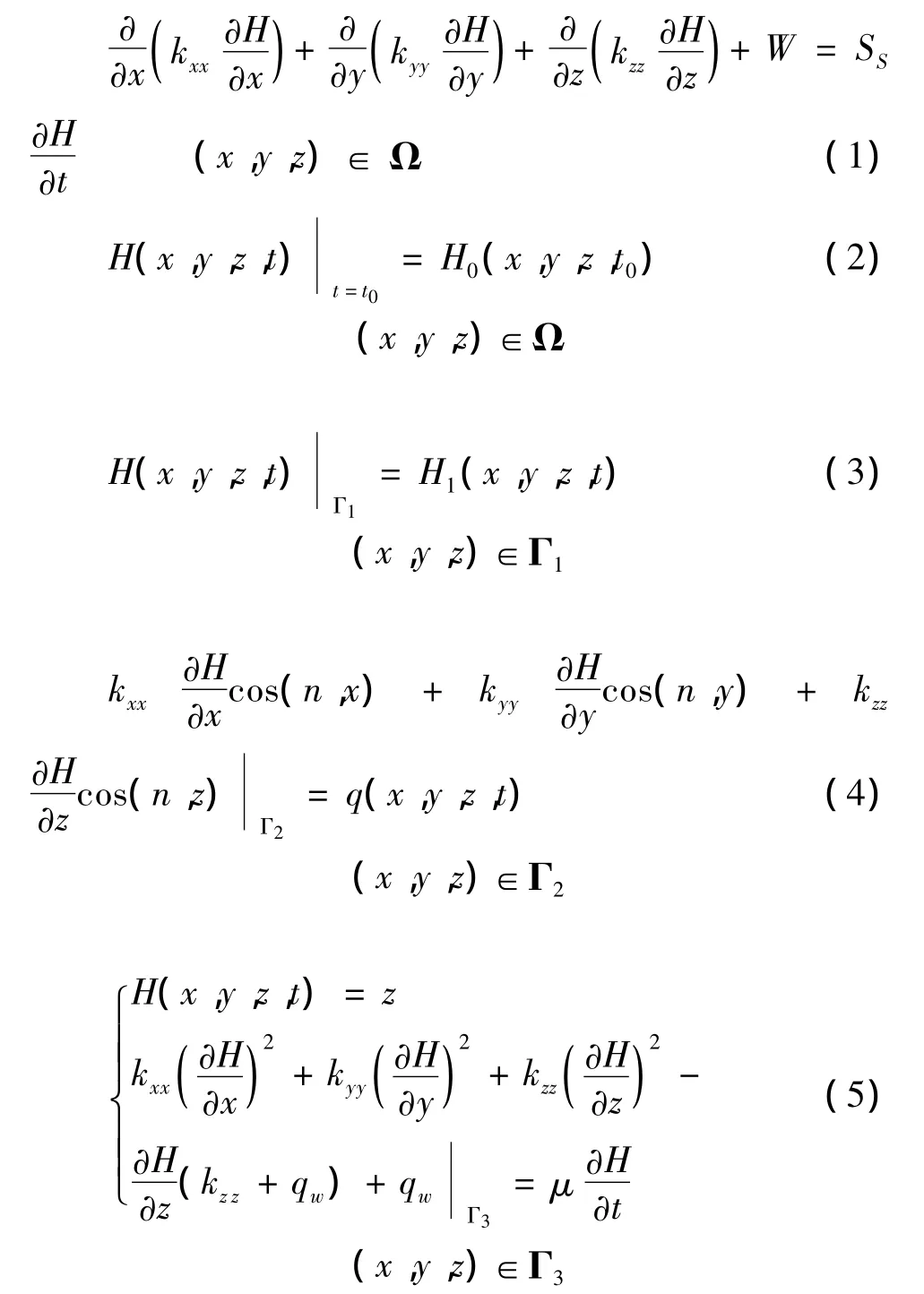
式(1)、(2)、(3)、(4)、(5)中,SS为储水率(1/m);kxx、kyy、kzz为含水层各向异性主方向渗透系数(m/d);h为点(x,y,z)在 t时刻的水头值(m);W 为源汇项(1/d);t为时间(d);Ω 为计算区;h0(x,y,z,t0)为点(x,y,z)处的初始水位(m);q(x,y,z,t)为第Ⅱ类边界上单位面积的补给量(m/d);h1(x,y,z,t)为第Ⅰ类边界上的水头值;cos(n,x)、cos(n,y)、cos(n,z)分别为流量边界外法线方向与坐标轴方向夹角的余弦;μ为饱和差(自由面上升)或给水度(自由面下降),它表示在自由面改变单位高度下,从含水层单位截面积上吸收或排出的水量;qw为自由面单位面积上的大气降雨入渗补给量(m/d);Γ1、Γ2、Γ3分别为第Ⅰ类边界、第Ⅱ类边界和自由面边界。
2.1.2 地面沉降数学模型(T J Burbey) 由地下水位下降引起的含水层压缩量的计算模型如下。
承压含水层的弹性变形量:

承压含水层的非弹性变形量:

潜水含水层的弹性变形量:

潜水含水层的非弹性变形量:

式(6)、(7)、(8)、(9)、(10)、(11)中,Δb 为含水层弹性变形量(m),正为压缩,负为扩张;Δb*为含水层非弹性变形量(m),正为压缩,负为扩张;Δh为水头变化值(m);Sfe为骨架成分的弹性储水因子(无量纲);Sske为骨架成分的弹性储水率(1/m);Sfv为骨架成分的非弹性储水因子(无量纲);Sskv为骨架成分的非弹性储水率(1/m);b0为可压缩含水层的厚度(m);n为孔隙率;nw为水位以上作为多孔介质总体积的一部分的湿气容量;G为剪切模量;ν为泊松比;Cc为压缩指数;p'为初始有效应力;e0为初始孔隙比;ρw为水的密度。
在沉降模型中,含水层及包含在其中的弱透水层被视为一个整体,假设整个含水层的骨架都可发生压缩并产生沉降作用,参数Sfe、Sfv是在整个含水层规模上的等效参数。
当各含水层的压缩量确定后,总地面沉降量也由此而求出。
上述二模型通过水头项耦合起来,即可形成基坑降水与地面沉降模拟预测耦合模型。该模型可用有限差分法和有限元法进行求解,并采用强隐式法(SIP)联立迭代求解代数方程组。模型求解通常分两步进行,先由水流模型求出水位,作为沉降模型的边界条件,再进行计算土层沉降变形,反复迭代循环计算,以实现水流和沉降的耦合。
骆祖江等(2007)应用上述模型研究了上海环球金融中心的深基坑降水问题,该基坑为直径100m的圆形基坑,开挖深度为26m,接近第Ⅰ承压含水层的顶板。通过该模型模拟预测,实现了该基坑降水的优化设计,取得了良好的效果。
笔者2008年应用上述模型研究了南京长江第四大桥北锚碇沉井基坑降水问题,根据基坑地下水位的控制要求,同时模拟计算出了降水井的布局、各井的开采量和地面沉降量,并据此确定出了基坑的降水方案,获得了成功。
2.2 地下水渗流与地面沉降三维全耦合模型
地下水开采引起的地下水渗流场发生变化实际上是一个渗流场和应力场相互影响、相互作用的过程。以比奥固结理论为基础,并考虑土体的非线性特征及土的渗透性随应力状态的动态变化,建立的地下水渗流与地面沉降三维全耦合模型,更加贴近实际,具有更高的计算精度。
2.2.1 比奥固结理论 饱和土体中假定土骨架变形为线弹性、微小变形、渗流符合达西定律、水不可压缩或微压缩的三维比奥固结方程如下(骆祖江等,2005)。

式(12)、(13)中,G 为剪切模量;ν为泊松比;wx、wy、wz分别为x、y、z方向上的位移分量;u为孔隙水压力;kx、ky、kz分别为 x、y、z方向上的渗透系数;γ 为土的重度;γw为水的重度。
上述方程结合一定的定解条件(初始条件和边界条件),即可进行求解。
2.2.2 定解条件 (1)初始条件。
①地应力初始条件
采用土体的自重应力估算土体的初始应力:

式(14)中,z为计算点深度;K0为静止侧压力系数,

式(19)中,μ为土体给水度;θ为自由面外法线方向与垂线的交角。
2.2.3 模型中有关参数与物理量的处理 (1)邓肯-张非线性模型。采用邓肯-张非线性模型,将土体的本构关系推广到非线性,则本构关系{Δσ}=[D]{Δε}中,矩阵[D]中的弹性常数 E、ν不再视为常量,而是随应力状态改变,其切线弹性模量和切线泊松比的表达式如下。

式(20)、(21)中,c、φ 为强度指标,k、n、Rf、G、F、D为试验参数,由土体常规三轴压缩试验确定。
(2)渗透率k的动态模型。流固耦合实际上是孔隙应力消散引起土体骨架应力重分布,宏观上表现为土体的固结变形,土体的孔隙率n改变,影响渗透率,从而影响渗流。目前许多流固耦合的文献建立的模型大都忽略孔隙率和渗透率之间的相互联系和变化。在比奥固结理论假定前提下,可以得到孔隙度φ和渗透率k的的动态表达式。
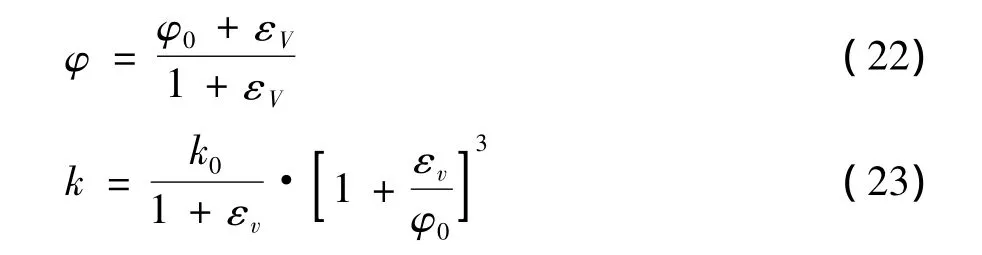
式(22)、(23)中,φ0为初始孔隙度;k0为初始渗透率;εV为体应变。
上述模型从机理上将地下水渗流与土体变形耦合起来,该模型由于涉及的参数较多,求解相对较复杂,目前还极少用于基坑降水与地面沉降模拟预测研究。该模型可用有限单元法进行求解,并采用预处理共轭梯度法迭代求解代数方程组,同时求出地下水位和地面沉降值,具有较高的精度。
骆祖江等(2005)应用上述模型研究了上海地铁四号线董家渡段隧道修复基坑的降水研究,该基坑基宽19m~23m,长236m,总面积2 290.7m2,开挖深度为40m,基坑底板已进入第Ⅰ承压含水层。通过该模型模拟预测,实现了该基坑降水的优化设计,在满足基坑降水的同时,有效控制了周边的地面沉降,获得了巨大成功。
3 结语
基于地下水动力学原理的解析解模型(Theis公式或Dupuit公式),由于模型自身假定条件及其对水文地质条件和降水工程刻画能力的限制,尤其是不能模拟计算由基坑降水引起的土体变形问题,已不适用于目前开挖深度大、水文地质条件及结构和施工复杂的大型基坑降水的模拟计算,尤其不能将此计算作为基坑降水方案设计的依据。
基于地下水三维渗流、太沙基一维固结和比奥固结理论的基坑降水和地面沉降耦合模型方法能够很好地模拟三维地质体及其整个基坑降水工程的结构与过程,可根据基坑地下水位的控制要求,同时模拟计算出降水井的布局、各井的开采量和地面沉降量,并据此确定出基坑的降水方案,具有重要的工程实用价值。
骆祖江,刘金宝,李朗.2005.第四纪松散沉积层地下水疏降与地面沉降三维全耦合数值模拟[J].岩土工程学报,27(1):48-54.
骆祖江,李朗,曹惠宾.2006.复合含水层地区深基坑降水三维渗流场数值模拟——以上海环球金融中心基坑降水为例[J].工程地质学报,14(1):72-77.
骆祖江,张月萍,刘金宝.2007.深基坑降水与地面沉降控制研究[J].沈阳建筑大学学报:自然科学版,23(1):47-51.
毛昶熙.2003.渗流计算分析与控制[M].北京:中国水利水电出版社.
钱家欢,殷宗泽.1996.土工原理与计算[M].北京:水利水电出版社.
薛禹群,朱学愚.2000.地下水动力学[M].北京:地质出版社.
张阿根,魏子新.2005.中国地面沉降[M].上海:上海科学技术出版社.
BURBEY T J.2001.Stress-strain analyses for aquifer-system characterization[J].Ground Water,39(1):128 -136.
Studies on simulative and predictive coupling model for deep foundation pit dewatering and land-subsidence in Yangtze River Delta region
DAI Gen-bao,YANG Min
(Jiangsu Geological Engineering Company Ltd,Nanjing 210018,China)
Deep foundation pit dewatering is complex and geological disasters are easily caused by land subsidence in Yangtze River Delta region.The traditional analytic solutions(Theis formula or Dupuit formula)of groundwater dynamics were difficult to meet the needs of simulation and calculation in the design of simulation,particularly hard to predict the land subsidence caused by dewatering.According to the control requirements of groundwater level,the layout of dewatering wells,discharge and land subsidence could be simulated and calculated by deep foundation pit dewatering and land-subsidence coupling model which coupled together with groundwater flow model and the soil stress-strain model.Accordingly a foundation pit dewatering scheme was achieved,which met the control requirements of groundwater level and optimal control for land subsidence.
Foundation pit dewatering;Land subsidence;Optimization design;Yangtze River Delta
P642.26;TU463
A
1674-3636(2011)01-0045-05
10.3969/j.issn.1674-3636.2011.01.45
2010-11-04;编辑:陆李萍
戴根宝(1964—),男,高级工程师,长期从事水文地质、工程地质专业工作,E-mail:dgb1964@163.com
