噪声混沌神经网络在TSP中的应用研究

刘开健，何碧贵，毛安定，孙幸福

(1.长江大学 电子信息学院，湖北 荆州434023；2.重庆电子工程职业学院，重庆401331；3.中国人民解放军77538部队政治处，西藏拉萨850000)

噪声混沌神经网络在TSP中的应用研究

刘开健1，何碧贵2，毛安定3，孙幸福3

(1.长江大学 电子信息学院，湖北 荆州434023；2.重庆电子工程职业学院，重庆401331；3.中国人民解放军77538部队政治处，西藏拉萨850000)

分析了NCNN(噪声混沌神经网络)模型的几个重要参数对系统性能的影响，并对其进行了优化。仿真结果表明，优化的算法能成功解决旅行商问题，比传统的依靠经验选择参数的方法更有效，在收敛速度同解的质量之间取得了很好的折中。

NCNN；TSP；收敛速度；解的质量

1 引言

TSP是一个典型的NP-hard（非确定性多项式）完全问题，自从1985年 Hopfield和Tank用 Hopfield人工神经网络(HNN)对其进行有效求解以来[1]，人工神经网络被认为是解决复杂组合优化问题的有效方法之一[1-4]。但HNN在稳健性、优化率以及收敛速度等方面仍然存在许多问题，因此，人们提出了许多改进方法。Wang等综合了随机模拟退火（SSA）和混沌模拟退火（CSA）算法的优点，提出了一种新的随机混沌模拟退火（SCSA）算法，即噪声混沌神经网络[2]。该算法具有十分复杂的混沌动力学特点，利用其遍历性和随机性进行搜索，同时引入随机噪声，再由退火策略控制混沌动态和噪声逐渐消失，保证网络能有效收敛和跳出局部最优，从而找到最优解。该算法的参数设置非常灵活，不同的优化问题具有不同的权重因子，因此，本文就NCNN的参数设置问题进行探讨和优化。

1.1 TSP问题描述

旅行商问题 （TSP）是指已知多个城市之间的相互距离，如：现有一位推销员必须遍访每个城市，并且每个城市只访问一次，最后必须返回出发城市。如何安排访问次序，才能使其旅行路线的总长度最短。这是一个典型的组合优化问题，该问题描述如下：

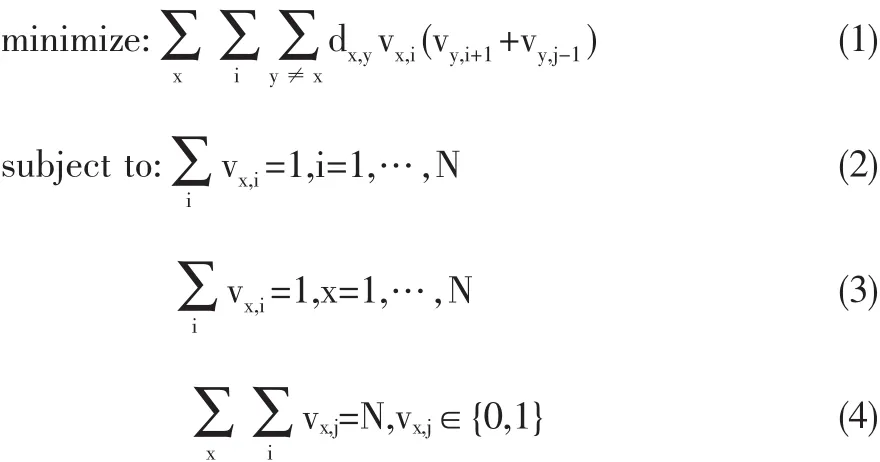
其中，x和y表示城市，i和j表示访问次序，dx,y表示x城市和y城市之间的距离。vx,i表示访问交换矩阵，即vx,i=1表示第i次访问x城市，否则vx,i=0。（1）式表示TSP问题的目标函数，即总闭合路径最短；（2）式表示行约束，即每个城市最多而且只能被访问一次；（3）式表示列约束，即每次只访问一个城市；（4）式表示N个城市一共只能被访问N次。

2 NCNN的TSP实现

2.1 能量函数

由HNN演变而来的NCNN的能量函数表示如下：

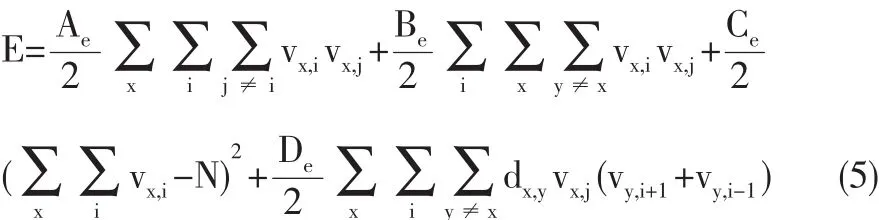
其中正常数Ae、Be、Ce和De为权重因子，E中前三项分别为（2）-（4）式对应的约束项，当系统收敛至平衡点后，这三项为0。表示每行每列恰有一个1，且矩阵V的各元素之和为N，表示N个城市恰被访问N次。最后一项表示目标函数（1）式，当系统收敛至稳定状态后，该项为正的最小值，即使NCNN继续运算，该项也不再减小。

2.2 动能方程

由系统稳定条件推出应用于 TSP问题的噪声混沌神经网络系统的动力学演化方程如下：

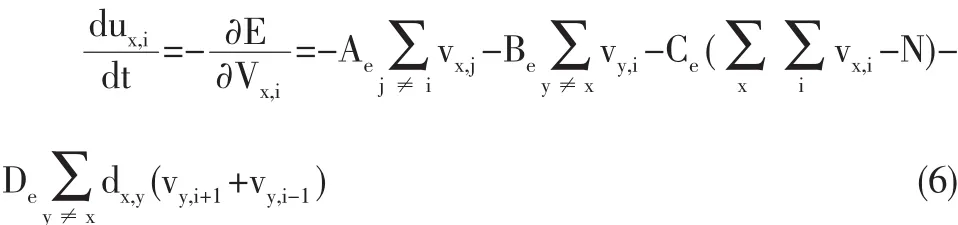
其中，Ux,i(t)和Vx,i(t)分别为t时刻神经元xi的内部状态输入和输出。其关系由S函数表示如下：

u0为神经元激活函数的增益因子。

为了在计算机上运行该系统以求得最优解，我们首先用欧拉方法建立(6)式的离散时间模型，然后加入负反馈产生暂态混沌动力，最后加入白噪声获得NCNN的离散时间模型如下：

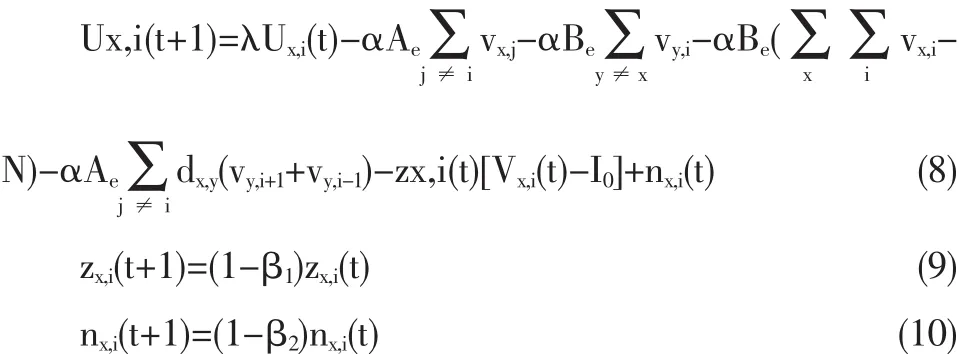
其中，λ为抑制因子，α为缩放因子且＞0，I0是一个正常数，zx,i(t)为负反馈联接权值，nx,i(t)是随机噪声，取值范围是[-Am,Am]，β1和 β2是退火参数。

为了加速系统收敛，本文采用神经元输出矩阵的平均值作为阈值去激活神经元函数，使本来连续的输出离散化，尽快靠近0和1。

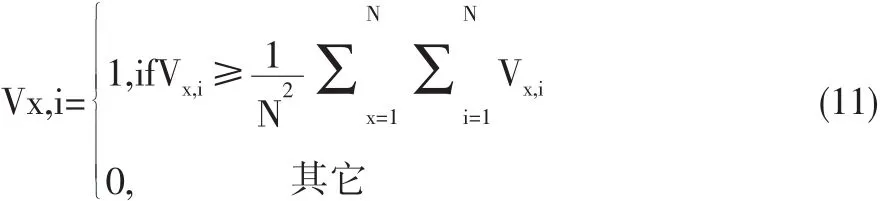
3 仿真结果分析

为了便于比较，本文同样采用Hopfield-tank模型[1]，用MTTLAB7.6进行仿真。为神经元激活函数的增益因子，是将每个神经元的内部输入映射为输出，直接影响到整个系统的各方面性能，所以该参数的选择至关重要。在很多文献中依靠经验选择，若太大，神经元输出快速收敛至0或1，近似离散函数，不利于混沌遍历搜索，易陷入局部最小值；若太小，搜索空间增大，但收敛速度变慢，如图1所示。所以本文基于系统收敛效率和解的质量的折中考虑，采用u0=10，这与前期文献有很大差别。

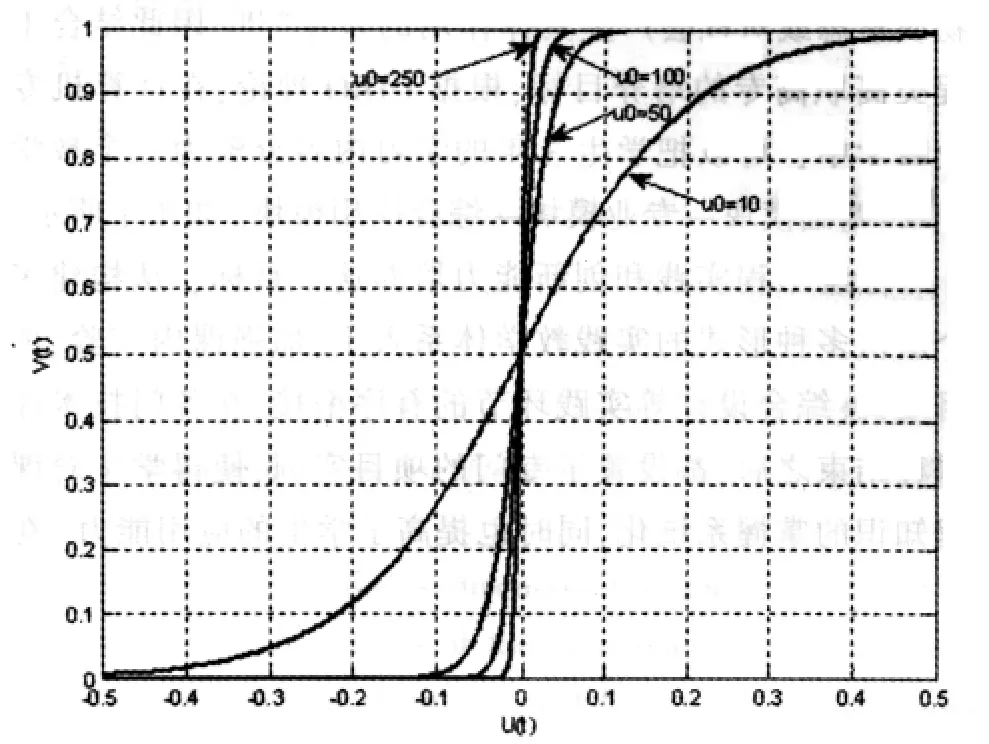
图1 不同激活函数的仿真效果

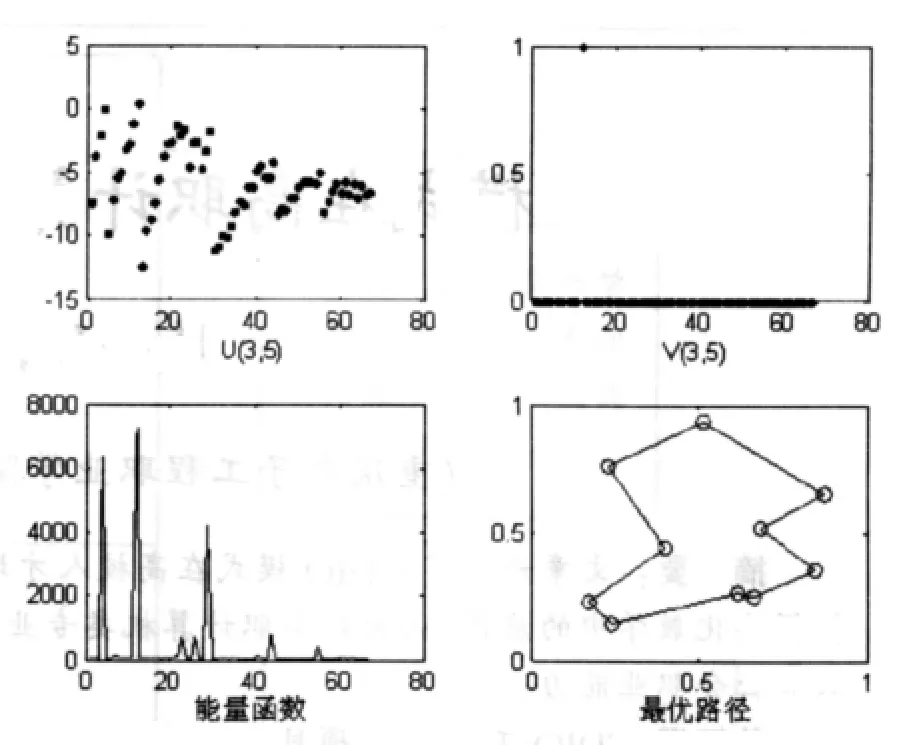
图2 Hopfield-tank模型的最优解

为了使负反馈对下次的神经元输入有足够的影响，同时为了能跳出局部最优，使系统能收敛到全局最优值，随机噪声也应该被加大，这样也有利于快速收敛。所以本文改变其常用值，将其设置为z0=0.85，Am=2。相应地，两个退火因子也同时被增加，但不能设置过大，否则优化率将大大降低，这里将其设置为β1=0.02,β2=0.02。本文NCNN模型的其他参数选择如下：α=0.05,I0=0.65,λ=0.95。四个权重因子分别设置为：Ae=3.5,Be=3.5,Ce=2.4,De=4.3。

将本文优化的参数用于Hopfield-tank模型，仿真1000次，每次最大迭代500次，仿真结果如图2所示。该系统平均迭代67次就能收敛到最优值，明显高于文献[2]中的124次。优化率为96.2%，略低于文献[2]中的99.4%。而且可以看到改进算法在混沌和噪声消失之前，系统已经收敛到稳定状态，大大提高了收敛速度；在系统收敛速度和解的质量之间取得了很好的折中。另外，我们随机选择了No(3,5)神经元，画出了它的内部状态（输入）U(3,5)和神经元输出V(3,5)，可以看出V经过离散处理后，与文献[2]中的V值已大大的不同。同时我们也画出了能量函数E的变化曲线，由于离散化的处理，它已经不再是很规则的梯度下降，但总的趋势还是呈下降趋势，直至系统收敛。

4 结 论

本文分析了NCNN的几个重要参数对求解最优值的影响，通过对其常用数值的调整，将其成功应用于TSP问题。仿真结果表明，优化的算法大大地提高了系统收敛速度，而且也获得了较高的优化率，在收敛效率和解的质量之间取得了较好的折中。

[1]J.J.Hopfield and D.W.Tank, “Neural computation of decisions in optimization problems”,Biol.Cybern.,1985，52（3）：141-152.

[2]L.Wang,S.Li,F.Tian,and X.Fu,“A noisy chaotic neural network forsolvingcombinatorialoptimizationproblems:Stochastic chaotic simulated annealing”,IEEE Trans.Syst.,Man,Cybern.,Part B:Cybern.,2004，34（5）：2119-2125.

[3]阎平凡.神经网络与模拟进化计算[M]．北京：清化大学出版社，2000.

[4]李敏，吴浪，张开碧．求解旅行商问题的几种算法的比较研究[J]．重庆邮电大学学报，2008，20(5)：525-528．

TP183

A

1674－5787（2011）04－0160－02

2011-06-15

刘开健(1981—)，女，重庆人，长江大学，讲师，主要研究方向：人工神经网络技术；何碧贵（1980—），女，重庆电子工程职业学院，讲师。

责任编辑 王荣辉