分数阶超混沌Lü系统的一步耦合同步研究①

隋丽丽王鲜霞刘瑞芹

(1.华北科技学院基础部，北京东燕郊 101601;2.太原理工大学理学院，山西太原 030024)

分数阶超混沌Lü系统的一步耦合同步研究①

隋丽丽1②王鲜霞2刘瑞芹1

(1.华北科技学院基础部，北京东燕郊 101601;2.太原理工大学理学院，山西太原 030024)

主要应用一步耦合法对分数阶超混沌Lü系统的同步进行研究和设计。利用拉格朗日终值定理证明了同步的有效性，并用数值仿真结果验证了同步的可行性。这种同步方法实现了分数阶超混沌系统初值不同的耦合同步。

超混沌，混沌同步，一步耦合

0 引言

1990年美国海军实验室研究员Pecore和Carroll首次证明并实现了混沌同步［1］，且在电路系统中观察到混沌同步现象［1］。次年，Pecore和Carroll再次提出了驱动－响应混沌同步方法，实现了两个混沌系统的同步［2］，从此混沌应用于保密通信中的研究成为可能。1991年4月，在日本联合大学和东京大学共同召开“混沌对科学与社会的影响”的国际会议，1991年10月，在美国召开了首届混沌实验研讨会。这些会议的召开促进了混沌学研究世界性热潮的到来。近十年来，人们先后发现或实现了混沌同步，目前，它更是与许多的学科相互渗透，得到了广泛的应用。同混沌控制同步的研究相比，人们对超混沌同步的研究可谓刚刚起步，超混沌的特点是至少在四维及更高维的非线性系统中具有2个或更多个正的Lyapunov指数，它广泛存在于自然界、流体、生物、经济等一大类高维非线性系统的众多领域中，在保密通讯及信息处理方面具有诱人的应用价值，因此更加吸引了人们的关注。

自然界中广泛存在着耦合振子，但目前已经提出的耦合同步方案大多限于整数维超混沌系统，大量研究表明［3－5］，当混沌系统的结果为分数时仍能出现混沌现象，并且更能反映系统的工程物理现象，从而促进了分数阶混沌系统的研究以及分数阶微积分理论的发展，分数阶超混沌系统的研究是更具有实际意义的行动。

一步耦合法的思想［6］：我们考虑两个分数阶混沌系统，f确定一个向量场，在第二个方程中加一个耦合项σu=(u－u')，构成如下的耦合系统：

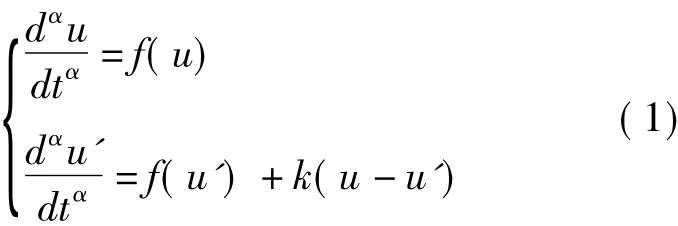
在耦合强度系统满足一定条件下可以实现系统的同步，这个方法中响应系统依赖于驱动系统的变化而变化，而驱动系统并不随响应系统的改变而改变。其中k是控制耦合系统反馈强度的变参数。

1 混沌同步的构造

在Caputo意义下分数阶超混沌Lü系统：

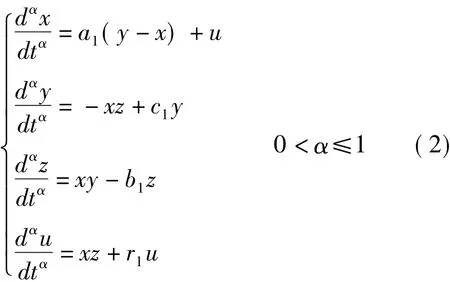
当参数a=36，b=3，c=12，r=－0.4，初值取x0=1，y0=1，z0=0，u0=3时分数阶Lü系统在α =0.94～0.98时系统的吸引子是超混沌的，其中0.98＜α≤1时分数阶Lü系统是周期的。上述参数不变，α=0.96时的Lyapunpv指数谱为：λ1= 0.0023，λ2=－0.002，λ3=0.0104，λ4=0.0115，有三个为正的Lyapunov指数，说明此时该系统的奇异吸引子是超混沌的。如下图分别给出α=0.96，α=0.99时分数阶Lü系统的超混沌吸引子与周期轨道。

我们把驱动系统用下标1表示，响应系统用下标2表示。

分数阶超混沌Lü系统的驱动系统为：

其中k1是耦合强度。

定理1令sα+a－k1≠0，在E2(s)，E4(s)有界的条件下，则驱动系统(3)与响应系统(4)可实现耦合同步。(其中E2(s)，E4(s)表示驱动系统与响应系统误差e2、e4的拉普拉斯变换)。

证明定义驱动系统(4)和响应系统(4)的状态误差为e1=x2－x1，e2=y2－y1，e3=z2－z1，e4=w2－w1，如果ei(i=1，2，3，4)随着时间的推移而趋于零，则表明两系统达到了同步;否则就没有达到同步。用方程(4)减去(3)，得到下面的误差动力系统：

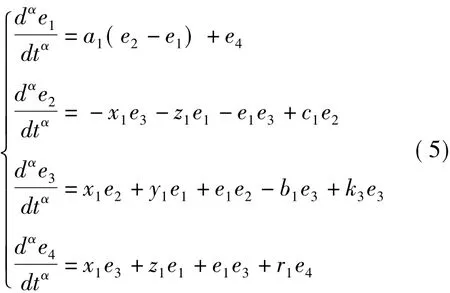
在方程(5)两端同时做拉普拉斯变换，令Ei(s)=L{ei(t)}(i=1，2，3，4)并根据L{dαei/dtα} =sαEi(s)－sα－1ei(0)［7］(i=1，2，3，4)，可以

得到：

2 仿真实例

为了验证上述方法的有效性，本文选取参数a=36，b=3，c=12，r=－0.3，α=0.96，显然分数阶Lü系统是混沌的，我们用预估校正算法求解(3)与(4)，用Matlab编程画出驱动系统与响应系统各分量差的图像，发现当驱动系统的初值取为x10=1，y10=1，z10=0，w10=3，响应系统的初值取为x20=0.5，y20=1，z20=1，w20=4，耦合强度选作k=－3时，可以实现上述驱动系统与响应系统的同步。图1给出k=－3时驱动系统与响应系统的各坐标误差：

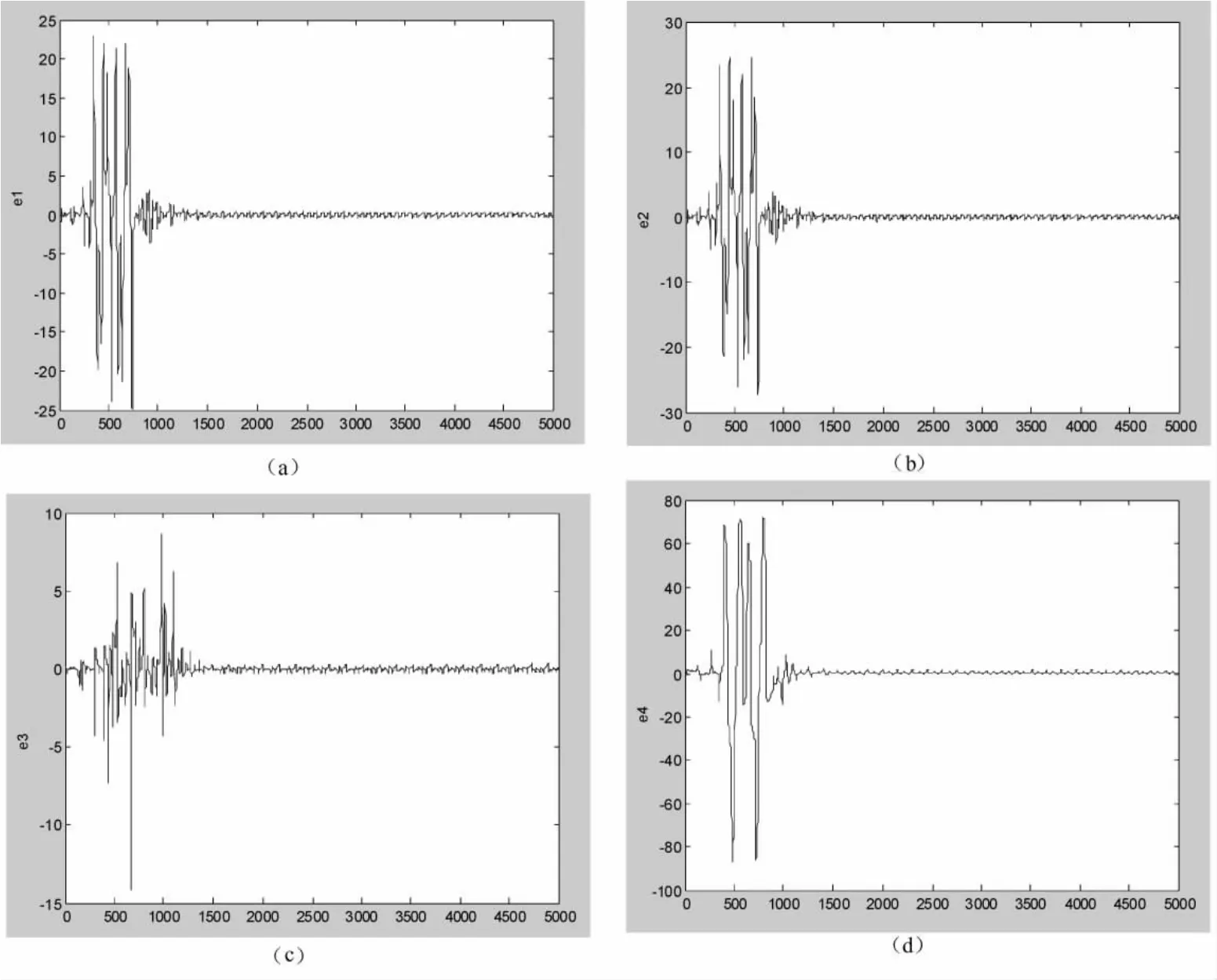
图1 k=－3时的分数阶超混沌Lü系统的ei随时间t的变化

3 结论

本文针对分数阶超混沌Lü系统，把实现低维空间中系统同步的一步耦合法推广到高维分数阶空间中，实现了分数阶超混沌Lü系统的耦合同步，这种同步方法易于实现、约束条件少、没有耦合系数大于零的限制，范围更广等优点。数值仿真进一步证明该方法的有效性。超混沌系统有两个或多于两个正的Lyapunov指数，其不确定性保密性更强，因此，超混沌系统的混沌同步在保密通讯中的应用前景是相当广阔的，耦合法有其特有的有点，渴望在保密通讯中大显身手。

［1］Pecora L M.Carroll T L.Synchronization in chaotic systems［J］.Phys.Rev.Lett.1990，64(8)：821－824

［2］K.B.Odlham，J.Spaniar，The Fractional Calculus［M］，Academic Press New York，1974

［3］Bagley RL，Calico RA.Fractional order state equations for the control of viscoelastically damped structures［J］.Guidance Control Dyn，1991，14 (2)：304－311

［4］Koeller RC.Application of fractional calculus to the theory of viscoelasticity［J］.Appl Mech 1984，51(2)，294－298

［5］Koeller RC.Polynomial operators，Stieltjes convolution，and fractional calculus in hereditary mechanics［J］.Acta Mech，1986，58(3－4)：252－264

［6］Wu Xiangjun.Chaos in the fractional order unified system and its synchronization［J］.Chinese physics，2007，16(7)：392－401

［7］M.T.Yassen.Synchronization hyperchaos of hyperchaotic systems［J］.Chaos，Solitions＆fractals，2008，(37)：456－475

［8］E.J.Muth.Transform methods with applications to engineering and operations research［M］.Englewood Cliffs：Prentice-Hall，1977

STUDY ON ONE-STEP COUPLING OFHAPERCHAOTIC Lü

SUI lili1，WANG Xianxia2，LIU Ruiqin1
(1.Dept.Of Foundation，North China Institute of Science and Technology，Yanjiao Beijing-East101601 2.Dept.of Science，Taiyuan University of Technology，Taiyuan Shanxi030024)

We maily design and research the synchronization of fractional hyperchaotic Lü system，we also prove the effectiveness of the synchronization using the final value theorem of Lagrange and demonstrate the feasibility of synchronization with numerical simulation results.This method of synchronization.This method achieved the coupled synchronization of the fractional order hyperchaotic system with different initial value.

hyperchaos;chaos synchronization;one-step coupling

0177.91

A

1672－7169(2011)01－0068－03

2010－12－21

隋丽丽(1983－)，女，硕士，华北科技学院基础部教师。