边坡稳定性的有限元数值模拟建模①

汪军刘海波

(华北科技学院土木工程系，北京东燕郊 101601)

边坡稳定性的有限元数值模拟建模①

汪军②刘海波

(华北科技学院土木工程系，北京东燕郊 101601)

本文针对国内某矿，考虑边坡材料的弹性和塑性，在不同的强度折减系数下，利用有限元法对该边坡进行稳定性计算分析，以判断其稳定性和计算出安全系数。由此可说明采用弹塑性有限元法进行计算具有独特的优势。

有限元;稳定性;数值模拟;建模

分析边坡稳定问题，基本上有两种方法：极限平衡方法和数值分析方法。极限平衡方法的关键是对滑体的体型和滑面的形态进行分析、正确选取滑面的计算参数，以及正确引用滑体的荷载条件等。因为极限平衡方法完全不考虑土体本身的应力应变关系，不能真实地反映边坡失稳时的应力场和位移场。本文用有限元的数值分析方法考虑土体应力应变关系，克服了极限平衡方法完全不考虑土体本身的应力－应变关系缺点［1－3］。

1 有限元法分析边坡稳定性计算原理

有限元强度折减法：首先选取初始折减系数，将岩土体强度参数进行折减，将折减后的强度作为参数输入，进行有限元计算，若程序收敛，则岩土体仍处于稳定状态，然后再增加折减系数，直到程序恰好不收敛，此时的折减系数即为稳定或安全参数。

强度折减法将强度折减技术与数值模拟方法相结合，在给定的评判指标下，通过调整折减系数对边坡的稳定性进行分析，求得边坡的稳定安全系数。其基本原理是将土体强度指标粘聚力c和内摩擦角φ值同时除以一个折减系数F［2－8］：

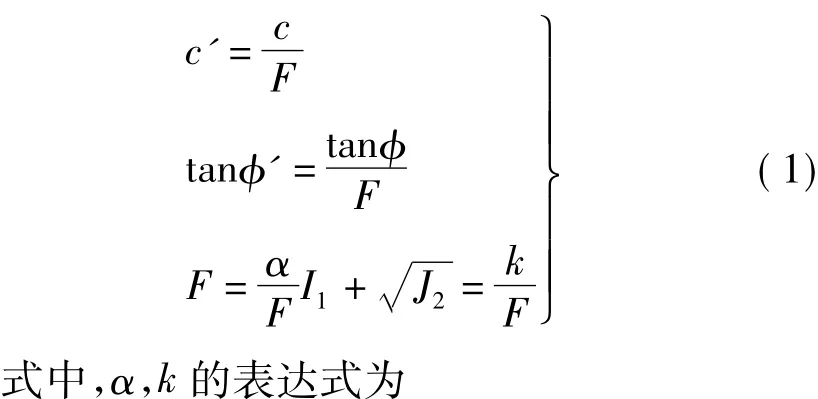
通过式(1)得到一组新的c'，φ'，作为材料新的参数进行数值计算，当边坡土体符合给定的临界破坏状态判定条件时，对应的F称为边坡的最小安全系数［9－12］。其中I1，J2分别为应力张量的第一不变量和应力偏张量第二不变量，不同的α，k是与c和φ相关的常数，不同的α，k在π平面上代表不同的圆。

2 工程算例

边坡实例选取国内某矿，该边坡考虑弹性和塑性两种材料，边坡尺寸如图1所示。分析目的是对该边坡进行稳定性计算分析，以判断其稳定性和计算出安全系数，该边坡围岩材料属性见表1。

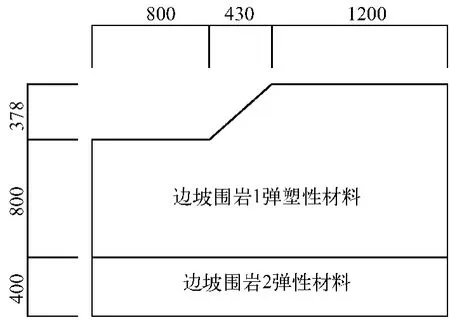
图1 边坡模型(m)

表1 边坡围岩物理力学参数

3 强度折减法分析确定边坡稳定性

3.1 计算模型的建立

计算假定边坡所承受的外力不随Z轴变化，位移和应变都发生在自身平面内。采用双层模型，模型上部为理想弹塑性材料，下部为弹性材料，左右边界水平位移为零，下边界竖向位移为零。网格划分情况：X方向划分为26个网格，Y方向划分为27个网格。根据上述相关资料有限差分网格如图2所示：

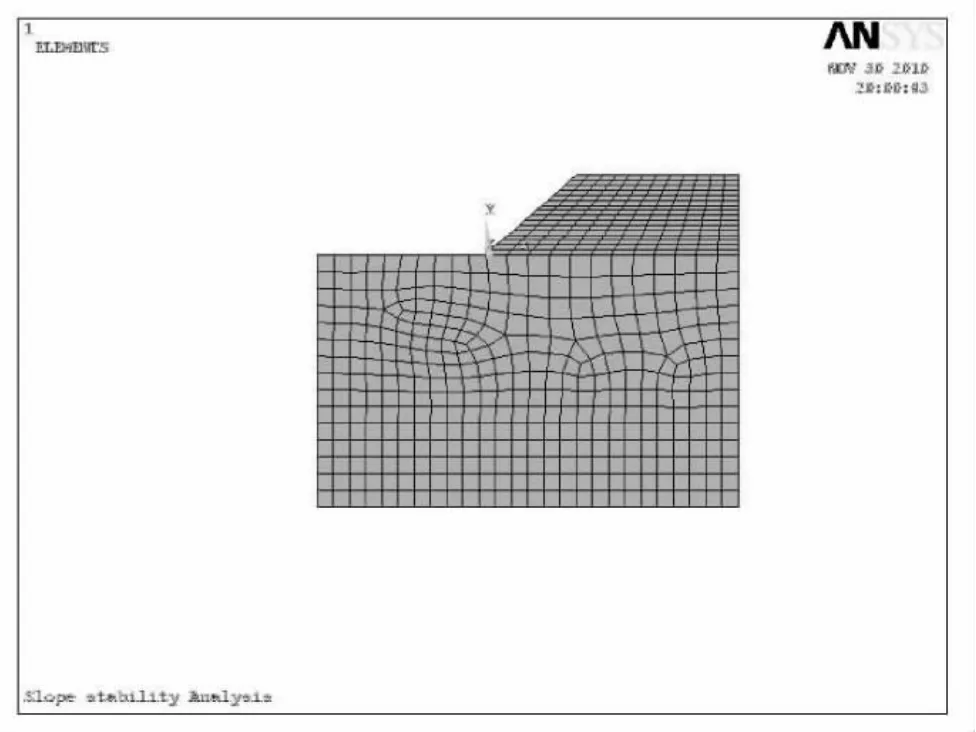
图2 有限元网格划分

3.2 有限元计算结果及分析

分别设置强度折减系数F为1，1.4，1.6，1.8……3.0，并依次求解，直到求解不收敛为止。

图3 F=1.2时边坡X方向位移云图

此时，边坡水平方向最大位移为58.815mm

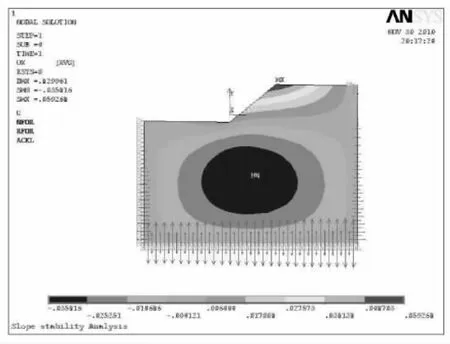
图4 F=1.4时边坡X方向位移云图

此时，边坡水平方向最大位移为58.811mm。

图5 F=1.6时边坡X方向位移云图

边坡水平方向最大水平位移为60.299mm

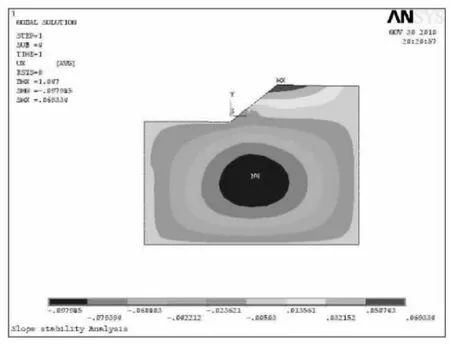
图6 F=2.2时边坡X方向位移云图

此时，边坡水平方向最大位移为61.972mm

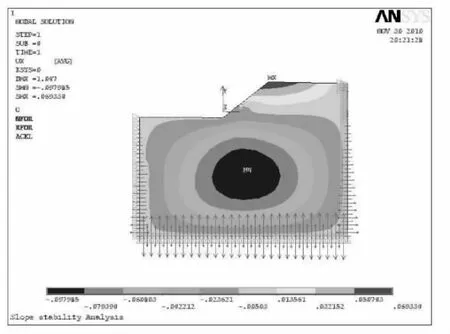
图7 F=2.4时边坡X方向位移云图

此时，边坡水平方向最大位移为55.284mm

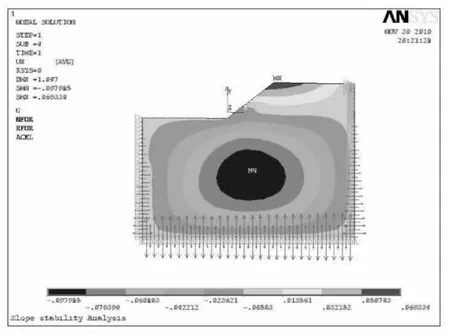
图8 F=2.6时边坡X方向位移云图

此时，边坡水平方向最大位移为48.001mm。由边坡塑性应变云图可看出，此时边坡模型有塑性应变，模型中塑性区逐渐扩大。

当F=2.8时，从边坡塑性应变云图可以看出，此时边坡模型有塑性应变，其值为11.46E－4，模型中塑性区逐渐扩大，很快就要贯通到顶坡。当F=3.0时，水平位移急剧下降，说明边坡已经破坏。模型中塑性区逐渐扩大，并贯通到顶坡。说明此时边坡已经不稳定了，也就是说边坡已经破坏了。

根据数值模拟结果可知，随着折减系数F的增大，边坡的塑性应变由坡体底部向上部扩展，当折减系数达到一定值时，整个边坡内塑性应变区从坡顶到坡脚即将贯通，可以认为在这之前的那个折减系数为边坡的安全系数。通过有限元强度折减法计算，当折减系数为2.80时，边坡处于临界破坏状态，再往下继续折减有限元程序计算不再收敛，由此确定边坡的安全系数为2.80。需要说明的是塑性区贯通并不等于完全破坏，当塑性区贯通后塑性发展到一定程度，再加上其他不利于边坡稳定的因素，土体会发生整体破坏，同时会生成其他贯通的塑性区。

4 结论

1)从边坡模型变形图分析

从边坡变形图看，随着强度折减系数F的增加，边坡变形加大，当F=3.0时，计算不收敛。

2)从边坡水平方向位移云图分析

边坡水平方向位移随着强度折减系数F的增加而发生很大波动，刚开始随

F增加，水平位移慢慢增大;当F=2.2后，边坡模型的水平位移开始减小;当F=2.8后，边坡模型的水平位移开始急剧下降;当F=3.0时，边坡模型水平方向位移下降到19.472mm，表明此时边坡已经破坏。

3)从塑性应变云图分析

从边坡模型的塑性区云图看，也随着强度折减系数F的增加，塑性应变从

无到逐渐增大，塑性区也从无到逐渐增大，当F=3.0时，此时结果不收敛，表明此时边坡已经破坏。因此，该边坡模型的安全系数应该是2.8。

［1］赵尚毅，郑颖人，时卫民.用有限元强度折减法求边坡稳定安全系数［J］.岩土工程学报，2002，24(3)：343－346

［2］赵尚毅，郑颖人，时卫民.用有限元强度折减法求边坡稳定安全系数［J］.岩土工程学报，2002，24(3)：343－346

［3］欧湘萍，白楷，朱云升.基于FLAC23D的强度折减法边坡稳定性分析［J］.武汉理工大学学报，2009，31(9)：59－61

［4］杨丽萍，宋子岭，吴野.拉格朗日元法及其应用软件FLAC在边坡稳定分析中的应用［J］.露天开采技术，2007，(2)：21－23

［5］GASMO J M，RAHARDJO H，LEONG E C.Infiltration effects on stability of a residual soil slope［J］.Computers and Geotechnics，2000，26(2)：145－165

［6］Manzari M T，Nour M A.Significance of soil dilatancy in slope stability analysis［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，2000，126(1)：75－80

［7］DAWAON E M，ROTH W H and DRESCHER A. Slope stability analysis by strength reduction［J］. Geotechnique，1999，(49)：835－840

［8］迟世春，关立军.基于强度折减的拉格朗日差分方法分析土坡稳定性［J］.岩土工程学报，2005，26(1)：42－46

［9］史秀志，陈小康，曾志林.极限平衡法与FLAC3D在边坡稳定分析中的应用对比［J］.现代矿业，2009，(3)：34－36

［10］Ugai K.A method of calculation of total factor of safety slopes by elasto-plastic FEM［J］.Soils and Foundations，1992，(3)

［11］Subhash Chandra.Under-reamed pile foundations in black cotton soils［J］.Indian concrete journal，1962

［12］Sliwinski Z，Fleming W G K.Practical consideration affecting the performance of diaphragm walls［C］//Anon.Proc.of the Conf.on Diaphragm Wall and A nchorages.London：ICE，1974：41－51

Slope stability of the finite element numerical simulation modeling

WANG Jun，LIU Haibo
(Department of Civil Engineering，North China Institute Of Science And Technology，Yanjiao Beijing-East，101601)

Consider elasticity and plasticity of the slope of two kinds of materials，in different strength reduction coefficient，by using the finite element method to the slope stability calculation and analysis，to judge its stability and compute safety coefficient. Which can be used to explain the elesto-plastic finite element method to calculate have an unique advantage

finite element method;slope stability;Numerical simulation;modeling

TU411.3

A

1672－7169(2011)01－0060－04

2010－12－18

汪军(1989－)，江苏进通人，华北科技学院土木工程系土木工程专业071班学生。