AF-PGM模型在大坝变形监测中的应用
2011-11-02吴良才
杨 磊, 吴良才
(东华理工大学测绘工程学院,江西抚州 344000)
AF-PGM模型在大坝变形监测中的应用
杨 磊, 吴良才
(东华理工大学测绘工程学院,江西抚州 344000)
基于目前灰色理论模型在变形监测中的应用,分析了PGM(1,1)模型中的参数及其求解的方法.引入人工鱼群算法求解背景值和初始值的修正项,通过人工鱼群算法求解得到模型的最优组合值。结合大坝变形监测工程实例进行计算分析,结果表明利用人工鱼群算法(AF)求解得到的PGM(1,1)模型的背景值参数与初始值修正项对大坝变形监测的预测具有较好的效果。
PGM(1,1)模型;背景值;初始值;人工鱼群算法
近年来,随着社会经济的发展,人类活动的加强,各种自然灾害频繁发生。为了减少灾害的影响,对大坝的变形监测就变成了一项重要工作,通过定期对大坝的坝体进行观测,分析其变形值和变形规律,并采取合理的方法科学预测大坝的变形大小,以便根据需要及时采取适当的预防或善后措施,确保大坝的安全使用。变形监测的预测模型和方法主要有泊松曲线预测模型、指数曲线法、灰色理论(邓聚龙,1988)预测、人工神经网络、双曲线法等。灰色理论得到了众多专家的深入研究,其灰色预测方法得到一定程度的认可。为此,笔者在前人对PGM(1,1)模型研究的基础上,将人工鱼群算法引入到PGM(1,1)预测模型中,对PGM模型中的背景值和初始值修正项采用人工鱼群算法进行全局寻优。
人工鱼群算法(李晓磊,2003;李晓磊等,2004)是一种基于动物行为的寻求全局最优的新思路,是行为主义人工智能的一个典型应用。它从构造动物简单的底层行为做起,通过各动物个体的局部寻优行为,最终在群体中使全局最优值突现出来。该算法具有良好的克服局部极值、取得全局组合最优值的能力,并且算法的实现无需目标函数的梯度值等特性,故其对搜索空间具有一定的自适应能力。并通过工程实例,说明该算法在参数估计方面的合理性和优越性。
1 改进的PGM(1,1)预测模型
1.1 非等间距数据处理
由于观测数据并不是等间隔的,PGM(1,1)模型输入的数据是等间隔的,这就要求首先对观测数据进行处理(陈鹏宇等,2010;刘金升等,2006)。具体步骤如下:
(1)计算各周期距首次周期的时间间隔:

为灰色微分方程的白化方程,即影子方程。
1.3 背景值重构

根据式(10)需要确定模型的参数a,b和比例因子p。对此非线性模型的参数估计有多种不同的方法,可采用人工鱼群算法(赖志坤等,2003;李大军等,2002)求解上述参数(表1)。
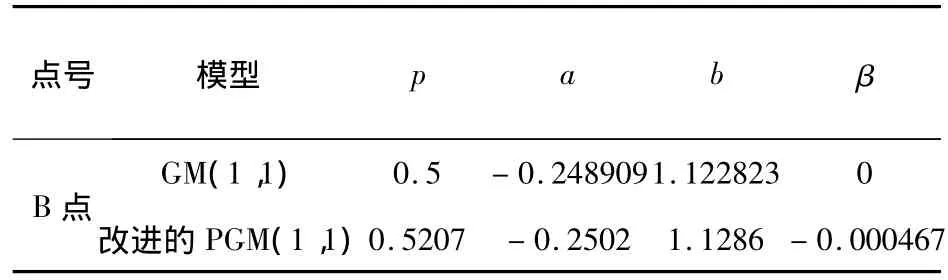
表1 B点的模型参数及初始值修正项Tab.1 The parameter of model and initial value of modification for point B
(2)将所求参数代入(12)式中可求得还原值为:
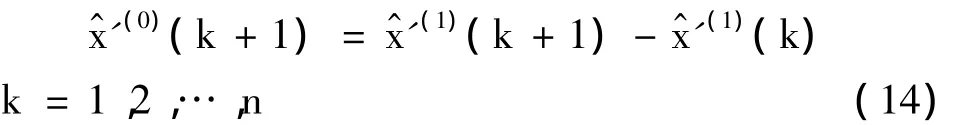
根据式(1)—(5)反算出对应的各周期的观测值。
1.5 精度检验


表2 精度等级评定Tab.2 Assessing the grade of precision
2 应用实例
本实例以某大坝边坡线上的点B在1985—1993年期间9a的变形值数据(史玉峰等,2002)为例建立预测模型来说明。分别取其前7a的观测数据进行建模,对第8年和第9年的进行预测。运用MATLAB进行编程,通过对前7a观测数据,运用GM(1,1)模型和改进的PGM(1,1)模型进行模拟,然后根据模型对第8年和第9年的变形值进行预测,并对它们进行精度评定(表3)。

表3 B的GM(1,1)预测模型和改进的PGM(1,1)预测模型Tab.3 The GM(1,1)model and modified PGM(1,1)model of point B
(1)通过计算,GM(1,1)模型的后验方差比值为0.016 3,而改进的PGM(1,1)模型为0.001 7,两组数据的P值均小于1.888 3,精度等级为一级。
(2)对表1进行分析发现,改进的PGM(1,1)不论是残差还是小误差概率P均远远小于GM(1,1)模型,由此可见改进的PGM(1,1)预测精度更高。
3 结束语
通过对PGM(1,1)预测模型背景值构造和初始值修正,减少了原始序列波动性的影响。通过实例可以得出改进的PGM(1,1)预测模型的精度在原来基础上大大提高。另外,后期可以探讨对数据采取新陈代谢的方法,保持数据量不变的情况下去掉早期数据;同时,通过表3观察预测数据存在正负交替出现的情况,还有待探讨。
陈鹏宇,段新胜.2010.建筑物沉降的非等间隔GM(1,1)模型的建立与改进[J].工程勘察,(3):77-80.
邓聚龙.1988.灰色预测与决策[M].武汉:华中理工大学出版社.
赖志坤,王新洲,朱欣焰.2003.PGM(1,1)预测模型及其参数估计[J].测绘通报,(11):14-16.
李大军,孙旭红,汤拥军.2002.PGM(1,1)灰色预测模型及其应用[J].华东地质学院学报,25(1):40-43.
李晓磊,冯少辉,钱积新,等.2004.基于人工鱼群算法的参数估计方法[J].山东大学学报,34(3):84-87.
李晓磊.2003.一种新型的智能优化算法-人工鱼群算法[D].杭州:浙江大学.
刘金升,左德元.2006.GM(1,1)模型与灰色Verhulst模型在路堤沉降预测中的探讨[J].岩土工程,26(1):69-73.
史玉峰,靳奉祥,马健.2002.参数修正法改进灰色预测模型及其在岩土工程变形信息分析中的应用[J].有色金属:矿山部分,54(3):26-27.
The Application of AF-PGMModel in Deformation Monitoring of Dam
YANG Lei,WU Liang-cai
(Faculty of Geomatics,East China Institute of Technology,Fuzhou,JX 344000,China)
Based on the GM(1,1)model in the deformation monitoring,the parameters of PGM(1,1)is analyzed and find the methods of solution.Bringing the artificial fish swarm algorithm for solving the background value and initial value of modifications,through calculating and analyzing the engineering example of the dam deformation monitoring.It shows that the obtained background value and initial value of modifications of PGM(1,1)model for using the artificial fish swarm algorithm have the batter precision to predict deformation monitoring of dam.
PGM(1,1)model;background value;initial value;artificial fish swarm algorithm
P207
:A
:1674-3504(2011)01-086-03
10.3969/j.issn.1674-3504.2011.01.014
2010-08-26
杨 磊(1985—),男,硕士,主要从事GPS变形监测数据处理。
