金红石相VO2电子结构与光电性质的第一性原理研究*

苏锐何捷陈家胜郭英杰

金红石相VO2电子结构与光电性质的第一性原理研究*

苏锐 何捷陈家胜 郭英杰

(四川大学物理科学与技术学院，成都610064)
(2010年11月13日收到;2011年1月12日收到修改稿)

采用完全势线性缀加平面波方法(FP-LAPW)结合密度泛函+U(DFT+U)模型计算了金红石相VO2的电子结构和光学性质．电子态密度计算结果表明所采用的方法可以较好的描述体系的导带电子结构．计算得到体系为导体，V—O键主要由O原子的2 p轨道与V原子的3 d轨道杂化形成，外加光场垂直和平行于c轴时体系的等离子振荡频率为3.44 eV和2.74 eV，光电导率在0—1 eV之间有一个与带内跃迁有关的德鲁德峰，而大于1 eV的光电导率主要由电子带间跃迁产生，得到并分析了带内跃迁过程和带间跃迁过程各自对反射谱和电子能量损失谱的贡献．

光电性质，电子结构，缀加平面波方法，VO2

PACS:71.15.Ap，71.15.Mb，77.22．－d，78.20．－e，78.20.Ci

1.引言

VO2在340 K附近存在着由低温下的单斜半导体相到高温下的体心四方金属相的转变［1］．由于其相变温度接近室温而在智能窗，红外探测［2］，激光防护，光敏元件等方面具有重要的应用前景．相关的实验制备［3］，光谱实验以及理论研究也得到了广泛的关注．实验上，Ruzmetov等人［4］对相变前后的VO2薄膜进行了X射线吸收谱测量．Muraoka等［5］对TiO2(001)面上生长的VO2薄膜进行了角分辨光电子谱的测量，得到了相变前后VO2的导带态密度．相变原理上，Mott等人［6］认为:VO2由单斜相向金红石相转变时氧八面体畸变减小，V原子所处的配位场对称性升高，导致d电子相互作用减弱而使体系由半导体相转变为金属相．这一理论已有基于声子谱的热力学计算结果支持［7］．

由于d电子间存在的强关联作用，使得基于单电子近似的密度泛函理论(DFT)难于准确描述过渡金属氧化物的电子结构．为了解决这一困难，可以采用DFT+U方法，通过附加一个半经验的电子间相互作用项U来改进DFT对过渡金属氧化物以及锕系金属氧化物［8］的计算结果．动力学平均场论(LDA+DMFT)［9］计算和基于多体微扰理论下的GW［10］计算也已表明考虑电子间的多体相互作用可以更好的描述VO2的电子结构和光电性质．

本文采用FP-LAPW方法［11］在广义梯度近似(GGA)下结合DFT+U方法计算了体系的电子结构和光学性质．比较+U前后电子态密度的变化，可以看到V原子的d电子关联作用对体系导带电子结构的计算结果具有较大的影响．在电子结构计算的基础上，进一步计算和分析了VO2的介电谱，光电导谱，电子能量损失谱等光学性质．

2.计算体系与方法

金属相VO2为体心四方结构，所属晶体群为P42/mnm(136)，X射线衍射实验［12］给出的晶格参数为a=b=4.530，c=2.869．V原子的Wyckoff坐标为(2a):(0，0，0)，(0.5，0.5，0.5)，O原子的Wyckoff坐标为(4 f):±(u，u，0)，±(0.5+ u，0.5－u，0)，u=0.30479．

本文中的计算是采用Dewhurst等人开发的完全势线性缀加平面波(FP-LAPW)计算程序elk［11］来进行．FP-LAPW方法将晶体势场划分为非交叠的原子中心的muffin球以及球间区域，在球内和球间区域分别采用球谐函数和平面波来展开电子波函数．计算中交换关联项采用Perdew，Burke以及Ernzerhof［13］提出的广义梯度泛函．k空间积分采用四面体方法．结构优化采用5×5×5的k点网格，自洽计算以及非自洽的电子结构和光学性质计算采用21×21×21的k点网格．平面波展开取为R× Kmax=7.0．其中R和Kmax分别为muffin球半径和平面波的截断波矢．计算采用的V原子和O原子的muffin轨道半径为1.8197 Bohr(a．u．)和1.5954 Bohr(a．u．)．

DFT+U计算方法采用Norman［14］提出的改进的计算方法，这一方法仅需U参数即可以确定DFT +U计算中所需要的各个Slater系数值［15］．计算中参考相关文献［9］将U值取为5.0 eV．为了验证这一U值的有效性，同时计算了U=2.72 eV和4.08 eV时的电子态密度以及U=5 eV时的单斜相带隙．DFT+U中的重复计算(double counting，DC)项采用Petukhov提出的［16］对AMF(around mean field)以及FLL(full localized limit)两种方法进行插值的方法来加以考虑．

对于金属体系，基于无规相近似(random phase approximation，RPA)的介电函数可以写作［17］

上式第1项为Kronecker符号，第2项为带内吸收项，第3项为带间跃迁项，Pi;n，n，k，Pj;n，n，k，Pi;c，v，k和Pj;c，v，k为动量算符的跃迁矩阵元．Ωc为原胞体积，εc，k和εv，k为单粒子态的能量本征值．为电子的费米分布函数对单粒子能量的导数，这一项表示只对费米能级附近的态求和．(1)式确定的带内吸收项在ω=0处有奇异性，在这一点定义等离子振荡频率［17］为

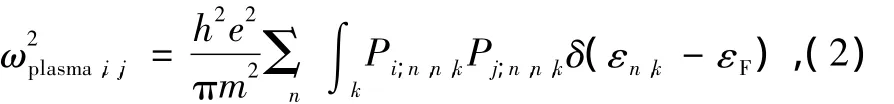
其中εF表示费米能级．实际计算中采用Drude模型计算带内吸收部分［17］式中Г为电子能级寿命导致的加宽效应．

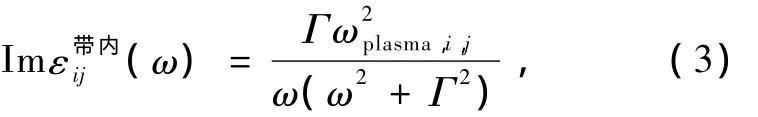
计算得到自洽的基态电子波函数后可得动量跃迁矩阵元．(1)式中的具有类似δ函数的特征，实际计算中通常对费米能级处的电子态密度进行展宽来考虑温度引起的电子态密度展宽．计算中可以使用Gauss型，Lorentz型以及Fermi-Dirac型等展宽函数．本文计算采用Gauss展宽函数，相应的展宽系数为0.272 eV，态密度和光学性质计算使用10个空带来进行．

光电导率实部可以由体系介电函数计算得到

相应的虚部可以通过Kramer-Kronig关系(KK关系)求出．同时电子能量损失谱(electron energy loss spectrum，EELS)以及反射谱与介电函数有以下关系:

3.计算结果

为了得到平衡态的晶体结构，首先在晶格参数实验值附近取5个点来计算体系的能量体积关系(E-V关系)，然后使用Vinet提出的的universal状态方程［18］对E-V关系拟合得到平衡态晶格参数，最后使用平衡态晶格参数保持体积和对称性优化得到各个原子的内坐标．结构优化时力的收敛标准为0.025 eV/．计算得到平衡态晶格的a=4.554，c =2.799，与实验值比较接近．

基于结构优化得到的晶格构型，在DFT和DFT +U下分别计算得到体系的总态密度和分波态密度．计算得到的结果如图1所示．图1(a)中画出了DFT和DFT+U(U=5.0 eV)下得到的总态密度结果以及DFT+U(U=5.0 eV)计算得到的分波态密度结果，同时还给出了实验得到的紫外光电子能谱(UPS)［19］和角分辨光电子谱(ARPES)［5］数据．图1 (b)给出了不同U值下得到的电子导带态密度．

从图1(a)的总态密度计算结果可以看到费米能级位于钒原子的d带内，体系表现为金属性．价带计算结果与通过紫外光电子能谱(UPS)［19］得到的实验结果符合较好，而且是否+U对价带计算结果影响很小．

比较图1(a)中分别采用DFT和DFT+U计算的导带态密度和通过ARPES实验［5］得到的导带态密度可以看到，+U后钒原子的t2 g带和eg带向上移动，同时t2 g带带宽增加了约0.5 eV．与ARPES实验［5］得到的导带态密度相比，DFT+U给出的t2 g带位置和带宽与实验结果符合得比较准确，两者的主要差别在于实验得到的谱峰高度以及费米能级处的态密度要小于计算结果．这一差别的原因有可能是实验测量采用的薄膜试样的表面电子态引起的，此时由于表面V原子的O配位体结构与体相情况有较大的差别而使钒原子的d电子态密度发生变化．

从图1(b)看，不同的U值对计算得到导带态密度有不同的影响．当U=2.72 eV时，由于电子关联作用较弱，DFT+U计算结果与DFT结果基本一致．当U进一步增加到4.0 eV时，费米能级左右两个态密度峰的峰间距由于电子关联作用由0.3 eV增大到1.0 eV．这一变化与U值的变化基本一致．然而此时在2 eV至2.5 eV之间存在带隙，这与光电子谱的结果是矛盾的．从光电子谱来看此时态密度虽然较小但并不为零．可以预见随着U的进一步增加，t2g带将上移，这一带隙将会消失．这正是U =5.0 eV时的情况．此时t2 g带和eg带向上移动，同时带宽增加，态密度减小，使得导带结构更加接近实际情况．总的来看，随着U的增大，d电子间的关联作用增强使得钒原子的d带上移，同时带宽增大，各能量处的态密度减小．为了进一步验证这一U值的合理性，在同一U值下计算了单斜相VO2的带隙宽度．计算得到带隙宽度为0.68 eV，与Cavalleri等人［20］给出的0.67 eV的实验值符合很好．因此所采用的DFT+U方法和U参数可以正确的描述VO2系统的电子关联性质．

根据光学原理，晶体的介电张量为一3阶对角矩阵，共有六个独立分量．对于体心四方结构，由于晶格对称性，沿a和b轴方向上的介电常数值相等．因此计算结果中只含有平行和垂直于c轴的分量．

图2给出了由(4)式计算得到计算得到的平行和垂直于c轴的光电导谱．光电导率在0—1 eV内快速的由6500Ω－1cm－1左右下降到1200Ω－1cm－1左右，这反映了导带自由电子的带内跃迁过程．随着能量升高，c轴方向上光电导在2.5 eV左右出现了一个与带间吸收相联系的光电导峰，而垂直于c轴方向在4 eV处才开始出现由带间吸收引起的光电导峰．超过5 eV后体系的带间吸收迅速增强，这一过程以占据态电子向空的p态和s态跃迁的带间吸收过程为主．计算结果与Qazilbash等［21］和Okazaki等［22］的实验测量结果相比，实验得到的带内吸收峰位于2 eV左右而计算得到的位于1 eV左右，这一差异是由于密度泛函理论描述导带的困难导致的．在带间吸收区域，实验谱［22］的谱峰位置和变化趋势与计算结果基本一致，而谱峰高度则有一定差别，由于这一差别是同一方向上的因此可以看作实验中的系统误差造成的．

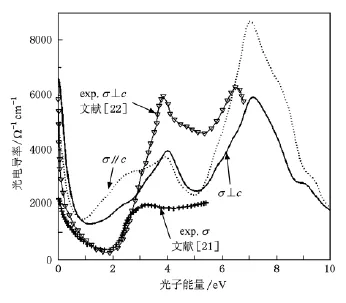
图2 光电导率计算和测量结果与实验结果［21，22］比较

由(2)式得到垂直和平行于c轴方向上的等离子振荡频率为3.44 eV和2.74 eV．Qazilbash等人［21］通过Al2O3衬底上生长的VO2薄膜的光电导谱得到的等离子振荡频率为2.75 eV而Okazaki等人［22］通过TiO2(001)面上生长的VO2薄膜的光电导谱得到垂直于c轴的等离子振荡频率为3.3 eV．由于Qazilbash等人［21］的实验中使用的是溶胶凝胶法生长的多晶薄膜，因此最后的测量结果应为两个方向上的光电导叠加．将实验光电导谱［21］中3 eV附近的带间吸收峰位置以及实验得到的等离子振荡频率［21］与计算结果比较，可以认为实验［21］得到的薄膜具有平行于c轴方向的择优取向．

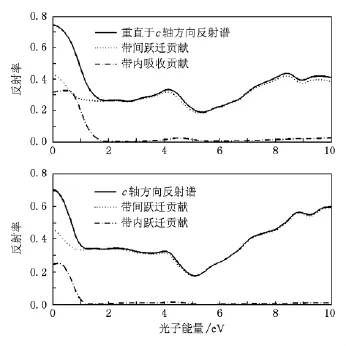
图3 光学反射谱

由(5)和(6)式计算得到光学反射谱(图3)和电子能量损失谱(图4)．图中同时给出了带内吸收和带间吸收的贡献．从图3看，垂直于c轴方向上的光反射率在0—2 eV区间内从大约75%下降到大约28%．然后逐渐上升，在4 eV处达到极大值35%后开始下降，之后在5.2 eV处达到20%的最小值，最后上升至45%左右并保持稳定．该方向上带内吸收与带间吸收的转换发生在1.8 eV左右．这一能量区间内以自由载流子的带内跃迁为主．当光子能量位于2—10 eV区域时，体系光学过程以带间吸收为主，带内吸收十分微弱．沿c方向上的反射谱与垂直于c方向的反射谱的变化趋势基本一致，主要差异在于c方向上带内—带间光学过程转换点位于1.1 eV左右．转换点的能量差为0.7 eV左右．与计算所得到的两个方向上的等离子振荡频率差值(0.7 eV)一致．

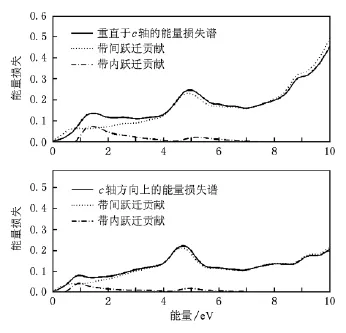
图4 电子能量损失损失谱

电子能量损失谱反映了电子以一定能量穿过物质的能量损耗．理论上的电子能量损失可以通过5式计算得到．计算结果如图4所示，图中同时给出了带内与带间光学过程的贡献．比较图3和图4可以看出两个谱图的谱峰具有相似性:当反射率较高时，光学吸收过程较弱，使得电子的能量损失减小．反之由于吸收过程增强，电子运动过程中需要损失更大的动能．

以上我们分析讨论了晶体的带内和带间光谱．然而基于群论分析［23］金红石相的VO2为极性晶体，具有三支垂直于c轴，一支平行于c轴的红外模式．在红外区域，晶格振动导致的红外光谱对总的光谱有一定贡献．然而密度泛函理论尚不能在光学计算中包括晶格振动引起的红外吸收．不过对于具有金属性的体系，在红外波段的带内吸收比较强烈，所以可以近似忽略这一部分贡献．

4.结论

采用PBE泛函优化得到了体系的稳定结构．在优化得到的晶格结构上，使用21×21×21的k点网格分别使用DFT和DFT+U(U=5.0 eV)进行自洽计算得到电子密度和波函数．在自洽计算基础上得到了DFT和DFT+U下的电子态密度．电子态密度结果表明V的3 d电子与O的2p电子的杂化形成了一个宽的带结构．计算得到的费米能级位于V原子的d带内，体系表现为类金属性质．为确定DFT +U方法以及所使用的U参数的合理性，将不同U值下的计算结果与实验结果进行了比较，并对单斜相VO2的带隙做了验证计算．结果表明采用的方法和参数可以恰当的描述计算体系．

光学性质计算得到体系的等离子振荡频率为3.44 eV(垂直于c轴)和2.74 eV(平行于c轴)．等离子振荡频率以及光电导谱与实验结果［20，21］符合较好．最后计算并分析了带间过程和带内过程各自对反射谱和电子能量损失谱的贡献．结果表明在低能量区域(小于2 eV)的光学反射主要由电子的带内跃迁导致．而更高能量区域的光学反射则由电子的带间跃迁所导致．

［1］Morin F J 1959 Phys．Rev．Lett．3 34

［2］Chen C H，Yi X J，Xiong B F 2001 Acta Phys．Sin．50 450(in Chinese)［陈长虹、易新建、熊笔锋2001物理学报50 450］

［3］Wang L X，Li J P，He X L，Gao X G 2006 Acta Phys．Sin．55 2846(in Chinese)［王利霞、李建平、何秀丽、高晓光2006物理学报55 2846］

［4］Ruzmetov D，Senanayake S D，Ramanathan S 2007 Phys．Rev．B 75 195102

［5］Muraoka Y，Saeki K，Yao Y，Wakita T，Hirai M，Yokoya T，Eguchi R，Shin S 2010 J．Electron．Spectrosc 181 249

［6］Zylbersztejn A，Mott N F 1975 Phys．Rev．B 11 4383

［7］Song T T，He J，Lin L B，Chen J 2010 Acta Phys．Sin．59 6480 (in Chinese)［宋婷婷、何捷、林理斌、陈军2010物理学报59 6480］

［8］Chen Q Y，Lai X C，Wang X Y，Zhang Y B，Tan S Y 2010 Acta Phys．Sin．59 4945(in Chinese)［陈秋云、赖新春、王小英、张永彬、谭世勇2010物理学报59 4945］

［9］Laad M S，Craco L，Mueller-Hartmann E 2006 Phys．Rev．B 73 195120

［10］Tomczak J M，Biermann S 2009 Europhys．Lett．86 37004

［11］http://elk．sourceforge．net/

［12］Morinaga M，Cohen J B 1979 Acta Crystallogr．A 35 975

［13］Perdew J P，Burke K，Ernzerhof M 1996 Phys．Rev．Lett．77 3865

［14］Norman M R 1995 Phys．Rev．B 52 1421

［15］Bultmark F，Cricchio F，Grn s O，Nordstr m L 2009 Phys．Rev．B 80 35121

［16］Petukhov A G，Mazin I I，Chioncel L，Lichtenstein A I 2003 Phys．Rev．B 67 153106

［17］Ambrosch-Draxl C，Sofo J O 2006 Comput．Phys．Commun．175 1

［18］Vinet P，Rose J H，Ferrante J，Smith J R 1989 J．Phys．: Condens．Matter．1 1941

［19］Goering E，Schramme M，Muèller O，Barth R，Paulin H，Klemm M 1997 Phys．Rev．B 55 4225

［20］Cavalleri A，Rini M，Chong H H W，Fourmaux S，Glover T E，Heimann P A，Kieffer J C，Schoenlein R W 2005 Phys．Rev．Lett．95 067405

［21］Qazilbash M M，Burch K S，Whisler D，Shrekenhamer D，Chae B G，Kim H T，Basov D N 2006 Phys．Rev．B 74 205118．

［22］Okazaki K，Sugai S，Muraoka Y，Hiroi Z 2006 Phys．Rev．B 73 165116

［23］Barker A S，Verleur H W，Guggenheim H J 1966 Phys．Rev．Lett．17 1286

First principles study of the electronic structure and photoelectric properties of rutile vanadium dioxcide*

Su Rui He JieChen Jia-Sheng Guo Ying-Jie
(College of Physics Science and Technology，Sichuan University，Chengdu 610064，China)
(Received 13 November 2010;revised manuscript received 12 January 2011)

The electronic structure and the photoelectric properties of rutile based VO2are investigated using the FP-LAPW method which is combined with the DFT+U method．The calculated density of statas(DOS)shows that the DFT+U method can describe the conductive band properly．The V-O bonding in VO2is induced mainly through the strong hybridization of V3 d orbital and O2p orbital．The calculated plasma frequency is 3.44 eV when the applied light field is perpendicular to the c axis and 2.74 eV when the applied light field is along the c axis．The optical conductivity spectrum shows a Drude-like peak is between 0 eV and 1 eV while in upper area the interband contribution is more important．Finally，the reflection spectrum and the election energy loss spectrum(EELS)are calculated and analyzed．

photoelectric properties，electronic structure，LAPW method，VO2

*国家自然科学基金(批准号:10875083)资助的课题．

．E-mail:hejie@scu．edu．cn

PACS:71.15.Ap，71.15.Mb，77.22．－d，78.20．－e，78.20.Ci

*Project supported by the Naional Natural Scfence Foundation of China(Grant No．10875083)． Corresponding author．E-mail:hejie@scu．edu．cn