以纠缠双光子多次穿过提高测量精度

尤林武 夏立新 伍方舟 刘双全

(河南科技大学 物理与工程学院 物理系，河南 洛阳 471003)

以纠缠双光子多次穿过提高测量精度

尤林武 夏立新 伍方舟 刘双全

(河南科技大学 物理与工程学院 物理系，河南 洛阳 471003)

文章研究了基于多次穿过相移器的双光束干涉仪，使用纠缠双光子进行相位测量。结果表明，能大幅度地提高测量精度，可打破标准量子极限。

纠缠光子；相位测量；光学干涉仪；标准量子极限

0 引言

到目前为止，有很多实验表明，测量精度可打破标准量子极限。但是，由于固有损耗的存在，其测量精度达到海森堡极限时，会随光子数的增加而变得更差[3,4]。如何提高物理量的测量精度已经成为物理学家的重要研究课题。

本文安排如下：在第1节中，介绍了Nagata干涉仪，使用纠缠双光子测量相位，对两种干涉仪的方案给出了统一的描述。在第2节中, 对两个方案的结果详细地进行了比较。最后，结论给出在第3节中。

1 两方案的统一描述

在Mach-Zehnder干涉仪的基础上，日本Nagata研究小组设计了一种干涉仪[1]，如图1所示，称其为Nagata干涉仪，简称为单次干涉仪。

图1 Nagata干涉仪示意图

Nagata干涉仪由一个束分器BS和三个单面平面镜1、2、3组成，它是单次 )(q=1穿过相移器PS的干涉仪。具体光路如下：

光由a，b第一次进入半透半反( 50:50 )的束分器BS，经过相移器BS作用后，一部分光向上传播，称其为模d，向上到达平面镜1，向右穿过PS(只单次穿过)到平面镜2，向下到平面镜3，向左到BS。

另一部分光称为模c向右到达平面镜3，向上到平面镜2，向左不穿过PS而到平面镜1，向下到BS。上述第二次到达BS的两束光，经过BS的作用后，向左输出的光为模e，向外输出的光为模 f。Nagata干涉仪具有超稳性，可保证模c和模d的光程差使子波长(纳米)稳定。但是，它只能使光束模d单次穿过相移器。

为了克服上述不足,我们改进Nagata干涉仪，使光束模d可多次穿过相移器，见图2，这样改进后具有多次穿过功能的干涉仪，称为多次干涉仪。

为了讨论的方便，下面，对基于单次和多次干涉仪进行的相位测量进行统一描述。

图2 模d多次穿过的示意图

设穿过相移器的次数为q，这里1≥q，在干涉仪的a，b两个输入端，同时输入单光子，就可产生双光子态,设 2=M 。双光子第一次穿过 BS 之后，由于Hong-Ou-Mandel效应[1,3]，双光子振幅干涉消除了项，

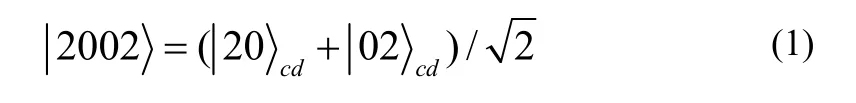
光子态为这就是我们所期望的纠缠双光子态。

如果模d穿过相移器q次(注意这里1≥q)，每个光子穿过一次产生未知的相移 后，光子态2002演化到

在模e和 f上，可探测两个光子的概率为

在实验中，有效粒子数为 qM = 2q，可计算标准量子极限[1]为

在理论上，根据概率方法，利用(3)式，可估算相位 ，其测量精度[1,2]为

在实验上,采用双光束干涉法[1]，其测量精度为

而对应的量子标准极限为

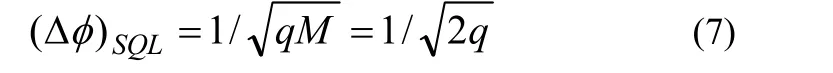
由(6)式和(7)式，可得其阈值可见度[1,4]为

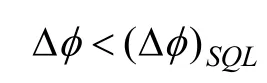
2 两方案结果的比较

下面，我们分别从理论和实验上来比较两种方案的结果。首先，我们从理论上来进行比较：

从上可知，两种方案都可打破标准量子极限。但是，由于'∆>∆，因此，多次穿过的方案所对应的精度要更高些。由(5)式可知，多次穿过的方案测得的精度会随着穿过次数q的增多而适当增大，因为在32≤q 时，光子损失很小[2]，测量精度可大幅度地提高。

接下来，我们再从实验上来进行比较：

① 如果采取Nagata干涉仪，即q =1，由(8)式，可得其阈值可见度为Vth≈70.7%。由文献[1]中的实验数据可知，实际测量的可见度为V=96%±1%。

② 如果采取多次干涉仪，即q≥ 2，由(8)式，可得其阈值可见度为 V 'th=50%。由文献[1]可知，实际测量的可见度可高达V'=90%±1%。

从上可知，两种方案都可打破标准量子极限，由于V 'th

3 结论

本文介绍了多次穿过相移器的干涉仪，其结构简单，光程差稳定性好，可保持在纳米量级稳定。多次穿过的方法可提高相位测量精度，以使用纠缠双光子为例进行了详细说明。结果表明，我们所提出的方案能大幅度地提高测量精度，可更好地打破标准量子极限。特别是，在当前的技术条件下, 本方案是完全可行的。

对于使用单光子、纠缠四光子和可区分的光子是否能打破标准量子极限？测量精度提高的幅度如何？这都是我们进一步研究的课题。

[1] T.Nagata, R.Okamoto, J.L.O’Brian, Beating the standard quantum limit with four-entangled photons [J], Science,2007, 316: 726-729.

[2] B.L.Higgins, D.W.Berry, Entanglement-free Heisenberg limited phase Estimation [J], Nature, 2007, 450: 393-396.

[3] F.W.Sun, B.H.Liu, Y.X.Gong, Experimental demonstra tion of phase measurement precision beating standard quantum limit by projection measurement [J], Euro physics Letters, 2008, 82: 24001 p1-p4.

[4]Z.Y.Ou, J.K.Rhee, L.J.Wang, Observation of Four-Photon Interference with a Beam Splitter by Pulsed Parametric Down-Conversion [J], Physical Review Letter, 1999, 83:959-962.

[5] V.Giovannetti, S.Lloyd, L.Maccone, Quantum Metrology[J], Physical Review Letter, 2006, 96: 010401 p1-4.

0431.2

A

1673-2219（2011）04-0023-02

2010－12－15

国家自然基金(No.10674018),湖南省自然基金(No.06JJ5015),中国博士后基金(No.20070420379)和河南科技大学人才培养基金(No.06025)。

尤林武 (1985－)，男，河南省林州市人，理学硕士，主要从事量子光学、量子计算和量子信息等方向的研究。

(责任编校：刘志壮)