地下通道箱涵墙裂缝原因分析

2011-10-27李凌居西安市第二市政工程公司

中国科技信息 2011年14期

李凌居西安市第二市政工程公司

地下通道箱涵墙裂缝原因分析

李凌居西安市第二市政工程公司

一、工程概述。

西大街地下通道工程位于西安市西大街洒金桥处，该通道施工时要求不影响西大街车辆正常行驶，箱涵长20.755米，宽6.0米，高3.0米。对缓解西大街行人通行有比较大作用。通道位于断面尺寸为净宽×净高＝6.0×3.0米的箱涵。底板厚0.4米，顶板厚0.4米，墙厚0.4米，两液角尺寸为0.4×0.4米。

施工顺序是：先浇筑底板和部分侧墙，因为考虑防渗砼，墙趾顶部设置凹槽，二次浇筑侧墙前进行了凿毛处理。2001年10月27日开始浇筑剩余侧墙和顶板，砼采用外加10.5%的UEA膨胀水泥，强度等级C35，采用泵送混凝土，砼坍落度控制在10～20厘米之间，浇筑完后仅对顶板采用塑料膜覆盖，洒水养护7d，侧墙配筋率0.84%。10月29日拆除外模并作防水层，11月11日拆内模，内外模均采用定型钢模板。11月11日之前未发现墙体砼开裂。2002年1月24日(距浇筑日期90d)，由首先发现侧墙裂缝，随即施工单位对裂缝进行了检查。裂缝情况如下：

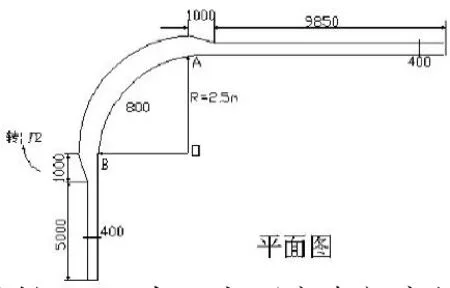
A缝长2.85米，上下窄中部宽约0.4毫米，上部至顶板液角中部尖。经现场监理同意凿开，裂缝深度5～6毫米，距终端水平长9.85米。B缝宽0.2毫米，两端细，距左终端弧线长 6.0米。

二、通道砼体产生裂缝原因分析

（1）定性分析

通道侧墙二次浇筑由于凹槽及二次凿毛处理，使新旧砼之间形成较强的外部约束。温度应力问题将约束分成两种形式，即外约束和内约束，外部约束为地基基础对墙体的约束；内部约束由于截面各点温度和收缩不同，收缩与非收缩之间形成内约束。内外约束在物体发生变形时均可引起结构产生内力。对一般构筑物工程而言，由于厚度尺寸均不很大，结构内部温度分布呈均匀分布。当受到外部气温骤降或均匀降时，均可引起结构形成表面（骤降）或深层（均匀降）性裂缝。集中反映在本工程二次浇筑砼后，由于温降即砼平均温度与大气温度之差，使砼产生收缩，但在基础部分受到老砼的约束，对墙体产生了阻止收缩的反力，墙体便产生了拉力。

可以这样考虑，通道侧墙应力计算采用下式[1]：

E——砼28d的弹性量3.15×104N／m m2。

α——砼线胀系数取1×l0-5

T——温差。T=TY+T0

L——墙体长度。

β——系数。

Cx称地基水平阻力系数，量钢kg／cm3取6 0，H为墙高。应力负号表示受压，正号表示受拉。该式坐标取墙长的中点，应力大小与温差、墙体长度及位置等情况有关，当x=0即位于墙体中点时，双曲函数c h β x=ch0=1有极小值，因此σx便有极大值。其他位置情况的应力，均比跨中小。

本工程L=20.755米，跨中L／2=10.39米，裂缝A发生在距右端9.85米处，与跨中10.39米只差0.54米，相对位置误差只有5.20%，由于中点应力最大，所以首先产生A裂缝，由于A缝产生，应力得到调解，在A缝与左端部之间尚有10.925米间距，其中点5.46米，而B缝位于其中点附近，其误差为6.0-5.46=0.54米，相对位置误差9.9%，此点仍有较大拉应力，因此B缝随后形成。水平应力σx超过砼抗拉强度时，在中部出现第一条裂缝，一侧墙分成两块，每侧墙又有自己的水平应力，但其最大值由于长度的减少而减少，如果该值仍然超过砼抗拉强度时，形成第二批裂缝，B缝就是第二批裂缝，从裂缝长度与宽度分析，均比A缝为小，说明水平应力σx比A点小，这便是长墙由于温度引起垂直开裂的有序性。另外，B点又位于变截面处，此处由于应力集中现象，一般容易产生温度裂缝。

（2）定量分析

在计算温降T时，应考虑砼的收缩当量温差Ty，与砼的温降差T0，即T=TY+T0。

当t=30d时

温差T0为砼平均最高温度与大气平均最低温度差，由于缺少实测温度资料，在无实测资料情况下，由下式决定。

砼蓄热养护至任一时刻t的平均温度T m：[2]

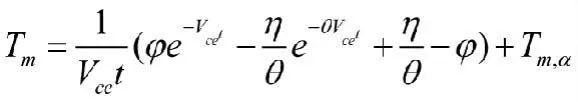
t——砼蓄热养护开始任一时刻的时间（h ）；

Tma——砼蓄热养护开始至任一时刻t的平均气温（℃）；

Vce——水泥水化速度系数(h-1)，在不考虑外加剂情况下取0.013；

φθη——综合系数，其表达式如下:

Cce——水泥累积最终放热量(K J／kg)，白鹿水泥P032.5R取330KJ／kg；

mce——每立方米砼水泥用量(k g／m3)，本工程采用配比380kg／m3及40kg／m3UEA膨胀水泥，因UEA膨长水泥含有30%SO，成份，故两者℃值不同，不考虑UEA的用量，取 =380kg／m3时，计算出的平均温度理论值偏低，对计算更偏于安全，有利于说明问题。

ω——通风系数，施工期取小风，ω=2.0；

ψ——结构表面系数(m-1)，对于墙体，Ac(砼结构表面面积)=115.45m2。V（砼结构总体积）=31.57m3

K——围护层总传热系数(KJ／m2.h.k)，本工程采用钢模板，10月27日浇筑，2010月29月拆外模。11月11日拆内模／m2.h.k；按裸露无保温计。

Pc——砼密度取2400kg／m3；

Cc——砼比热容(KJ／kg.K)，一般取Cc =0.94，参照《水工砼温控与防裂》一书[4]，可采用加权法求解。

水、普通水泥、石英砂、石灰岩、粉煤灰在21oC时的比热分别是4.1868、0.4564、0.6992、0.7494、0.92；五种料的重量比分别为7.1%、17.2%、27.45%、44.87%、3.28%；则Cc =4.1868×0.071+0.4564×0.1762+0.6992×0.2745+0.749×0.4487+0.92×0.0328=0.93与推荐值相近。

②对于那些建成年的建筑区来说，居民人数和居民用电负荷都没有达到饱和，我们将其称为半饱和状态，其负荷有很大的增长空间，进行预测时要根据城市用电的饱和系数进行；

T3——砼成型完成时温度，当天气温17.4℃。

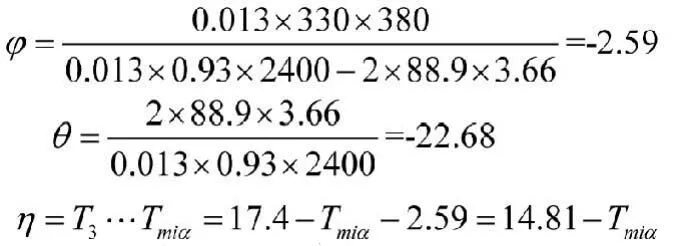
从10月27日砼浇筑至11月25日发生连续气温骤降的平均温度Tma。如表1。

根据公式[2]计算得出：T10,27=19.26℃，同样得出T10,28=17.66℃，……，T11,27=9.27oC,见表2。

计算10月27日人模时砼平均温度。如此计算至11月27日，结果如下：绘画10月27日浇筑砼至11月25日气温开始骤降时间的砼平均温度曲线如下：

以上分析，主要是由于外部约束，即侧墙地基阻力Cx对侧墙产生的拉应力使墙面开裂。

内部约束致使砼开裂的事件也常会发生，当暴露在空气中的侧墙遇到气温骤降袭击时，如11月25日～11月27日发生了三天气温骤降，日平均气温从11月24日的10.6℃，降止11月27日日平均气温1.2℃（见上温度曲线），降温9.4 ℃，而此时砼侧墙的平均温度Tm=9.27 ℃，砼内部温度比气温高8.07 oC，内部较热的砼约束了表面剧冷砼的自由收缩变形，由于时间短，加荷速度快(注：加荷速度与徐变有关，此时不能再用上述的应力松弛系数)，砼徐变性能不能发挥，约束强度接近100%，当拉应力超过其极限强度时，即出现表面裂缝。

以T0表示气温骤降幅度，在约束程度接近100%情况下，墙体实际发生的拉应力为,μ取1/6, T0=10.6o-1.2o=9.4 ℃，则σx=3.55N／mm2＞ft=1.43 N／mm2（其中ft为C30混凝土抗拉强度设计值），很明显引起侧墙表面开裂。砼均匀温降（第一种情况）及大气气温骤降（第二种情况），均可引起侧墙开裂。

三、关于箱涵补偿砼因素考虑

本工程采用了补偿收缩砼，当普通水泥外加8%～12%不等的UEA膨胀水泥后，经过14d的潮湿养护，其限制膨胀率ε=0.03%～0.05%是可以达到的。在定量分析中计算了砼的收缩量εY=0.33×10-4，ε-εY=0.027%，这就是说采用了补偿收缩砼后，其膨胀量是足以抵消其收缩量的，在量上相差了一个数量级，砼不会发生收缩，或收缩量大大减少，但为什么采用此措施后砼仍然开裂?原因是要达到补偿收缩砼的限制膨胀率平均在0.4‰，一个首要条件是14d的潮湿养护，由于侧墙垂直，11月11日拆内模时已历时15d，无法潮湿养护，其限制膨胀率达到否，不可而知。U E A膨胀水泥在不加湿养护条件下是不会发生膨胀的。国家标准要求，空气中养生28d的试件，限制膨胀率不小于-0.02%亦算合格，这就是说膨胀水泥在干燥情况下，不但不膨胀，反而有允许0.02%的收缩量。因此，在未潮湿养护条件下，其补偿收缩的意义没有实现，在计算收缩量εY时，不考虑UEA的膨胀作用是正确的。