超长混凝土结构温度应力分析

2011-10-26中国建筑东北设计研究院栗树文

河南科技 2011年18期

中国建筑东北设计研究院栗树文

超长混凝土结构温度应力分析

中国建筑东北设计研究院栗树文

现代建筑业中出现了越来越多体量巨大的建筑，其长度可达100～200m。规范规定：超过55m的框架结构应在其中部设置若干温度伸缩缝。但常常由于使用功能和构造上的要求，不适宜在建筑结构中设缝断开，因此不设缝的设计思想被越来越多的设计人员所认同。一般来说，结构越长，温度及收缩变形就越大，约束内力也就越大，往往引起结构开裂，影响其正常使用，此时超长混凝土的温度应力分析成为设计中的一个重要环节。温度作用（收缩）应力（内力）的计算与外荷载作用下的主内力计算不同，其值的大小取决于支撑形式及其抗侧移刚度，且两者互为因果关系。

一、温度应力计算原理

实际结构在环境温度作用下的应力分布、开裂形态是一个时变的、非线性的复杂问题，环境温度变化时，结构两侧分别向内收缩或向外膨胀，在结构的平面刚度形心附近存在一个不动点。距离不动点越远的地方，产生的变形越大。以图1所示的框架结构为例，在没有柱子约束的条件下，第i根柱子处的变形计算公式为：

式中，i为不动点为基准的柱子序号，l为框架跨度，Δt1为与混凝土成型时的环境温度相比较的变化量,αT为混凝土的热胀系数，一般为1×10-5m/(m·℃)。

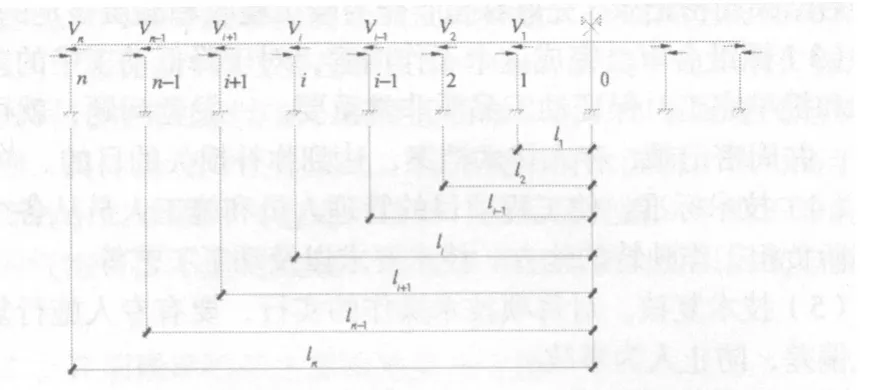
图1 某榀超长框架示意图

当楼盖与柱子整浇在一起时，楼盖的变形会带动柱子产生侧向位移。如果柱的上下端位移一致，柱子中将不产生内力。显然，为了协调这一变形，柱子上会产生剪力、弯矩等内力。这些因素相互作用，使实际各支撑柱处产生的变形比式（1）计算的略小。因此，如果柱顶、柱底处于不同的环境温度时，第i根柱子的剪力Vi可以由下式得出：

式中，Δt为柱子上下端所处的环境温度差；D为柱抗侧移刚度，根据结构力学公式，可得到D=12EcIc/ H3，式中H为柱子高度；Ec、Ic为柱子的弹性模量、惯性矩。而楼盖中的平均拉应力为：

式中，Nj为不动点起第j跨的楼盖轴力，A为楼盖横截面面积。柱子的剪力同时将引起弯矩，其峰值为：

式中，β为反弯点距离柱顶、柱底的距离与柱子高度的比值。

此弯矩由与柱子相连的框架梁（包括翼缘板）承担，对于顶层楼盖，中柱情况下，两侧梁刚度基本一致，弯矩由左右梁平均分配这一弯矩，而对于边柱，这一弯矩仅由一根梁平衡，因此，与中柱、边柱相连梁的最外层纤维所受到的弯矩拉应力分别为：σM,中=βHVj/ 2W，σM,边= βHVi/ 2W。可以预见，这一拉应力同时也会影响作为翼缘的楼板应力。

二、多层框架结构温度应力的特点

温度应力实际上是一种约束应力，约束应力包括内约束应力和外约束应力。引起温度应力的温度荷载一般可分为季节温差、骤然温差和日照温差等，长期缓慢的季节温度变化作用于结构整体，对结构的变形影响较大，依据大量的实践经验，多层钢筋混凝土框架结构的温度应力计算有如下特点。

1. 假定基础上地下室不变形，多层框架按两层计算（只考虑地面以上两层框架，顶层计算时只考虑顶部两层框架）。

2. 多层框架的最不利部位是变形不动点的横梁，此处承受着最大的轴拉力（收缩时）。假定是对称结构，结构中间部位横梁可能开裂，并且在下部1、2层开裂较严重；端部柱子承受着最大的弯矩和剪力，可能出现主根弯曲和剪切破坏，如图2、图3所示。

3. 多层框架中间部位横梁内力最大，变形最小，端部内力最小，变形最大。

图2 降温时典型框架的弯矩

图3 降温时典型框架的轴力（梁）和剪力（柱）

三、温度应力对楼板的影响

温度作用引起的板中应力可分为两部分，其一为轴向拉力引起的拉应力，其沿楼板横向截面基本均匀分布，沿楼板厚度方向也基本均匀分布，危害较大。其二为弯矩引起的拉应力，其引起的拉应力不会形成贯通裂缝，同时，开裂后内力将会发生重分布，由未开裂部分承担内力，影响要小得多。需要注意的是，温度作用下的弯曲应力将会与正常使用下的荷载作用相叠加，在不利组合下，会加剧、加速裂缝的发生和发展，特别是梁的支座截面。