一类分数阶混沌金融系统的复杂性演化研究*
2011-10-25辛宝贵刘艳芹
辛宝贵 陈 通 刘艳芹
1)(天津大学管理与经济学部,天津 300072)2)(山东科技大学经济管理学院,青岛 266510)(2010年6月21日收到;2010年8月2日收到修改稿)
的稳定性.系统
一类分数阶混沌金融系统的复杂性演化研究*
辛宝贵1)2)陈 通1)刘艳芹1)2)
1)(天津大学管理与经济学部,天津 300072)2)(山东科技大学经济管理学院,青岛 266510)(2010年6月21日收到;2010年8月2日收到修改稿)
物理学理论与方法在经济与金融领域中的成功应用催生了一个新的科学分支——经济物理学(econophysics).分数阶微积分系统的复杂动力学现象受到了越来越多学者的关注.本文定性地分析一类分数阶混沌金融系统的均衡解的稳定性及Hopf分岔发生的条件,并运用亚当斯-巴什福斯-莫尔顿预估-校正的有限差分法,通过分岔图、相图和时间序列图对该系统的复杂性演化行为进行仿真研究.
经济物理学,分数阶微分方程,金融模型,混沌
PACS:89.65.Gh,05.45.- a,02.30.Oz
1.引 言
El Farol Bar问题[1]与少数者博弈模型[2]的提出以及一些物理学的重要理论与方法在经济金融研究中的应用[3—7]具有划时代的学术意义,已经形成了一股强大的聚合力,对经济物理学学科的建立与推动产生了积极、有益的作用,其深远影响将随着时日变化、社会进步而愈见显著.
分数阶微积分算子理论在物理学中得到了成功应用,解决了许多物理学领域的问题[8—15].近十几年来,已经在物理学中成功应用的分数阶微积分理论在人文社会科学等领域也有了成功的应用,例如分数阶金融模型[16]、分数阶幸福模型[17]、分数阶爱情模型[18]等.
研究表明,经济和金融是人类参与的包含许多主体因素的极其复杂的非线性系统,存在许多整数阶微积分理论所不能描述的特性,因而,需要尝试运用分数阶非线性动力学的分岔、混沌等方面的理论,研究经济金融系统的内在复杂性,这方面的研究已经取得了一些前期成果[16].
混沌与分岔是存在于非线性经济金融系统中的一种复杂现象,系统由简单的状态,如均衡状态、周期性运动状态和拟周期运动状态,进入混沌状态的方式是非线性经济金融动力学研究的一个重要课题[19,20].经济金融系统中的混沌意味着系统本身具有内在的不稳定性,一般对经济系统是有害的.从目前的研究成果来看,前人通过定性分析和数值模拟等方法已经发现了四条具有代表性的通向混沌的道路:倍周期分岔通向混沌、阵发性通向混沌、拟周期通向混沌、KAM环面破裂通向混沌[21].
黄登仕和李后强[22]在分析宏观经济运行规律的基础上,建立了一个由生产子块、货币、证券子块和劳动力子块所组成的混沌金融系统,通过适当的坐标变换和量纲处理,得到了如下仅含有三个变量的模型:
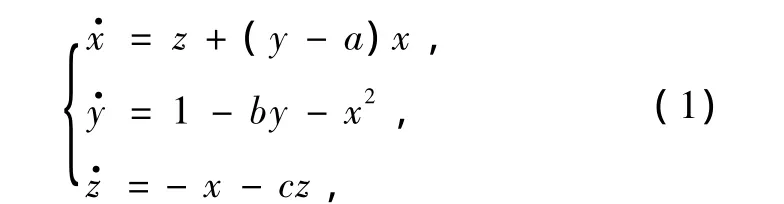
其中,x表示利率,y表示投资需求,z表示价格指数,a≥0为储蓄量,b≥0为投资成本,c≥0为商品需求弹性.
2.分数阶混沌金融系统的描述
国际货币基金组织总裁卡恩在出席2010年亚洲金融论坛时指出:相对于发达国家而言,新兴市场经济体的本土需求较富弹性,经济结构较佳,单位投资成本比较低[23].因而,对于系统(1),我们可以保守地认为c-b-abc>0是部分新兴市场经济体所具有的特点之一.
相对于新兴市场经济体而言,发达国家的经济结构较为成熟,本土的商品需求弹性不够高,而单位投资成本却相对较高.因而,对于系统(1),我们可以保守地认为部分非新兴市场经济体会具有cb-abc≤0的特点.
为了研究系统(1)的分数阶形式,本文采用如下 Caputo 微分形式[24,25]:

其中 n-1<α≤n,Γ(·)是 Gamma函数.
Chen[16]在混沌金融系统(1)中引入了分数阶微分的概念,并将其扩展成为分数阶混沌金融系统,如下面的自治系统所示:
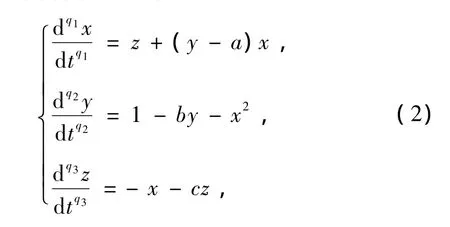
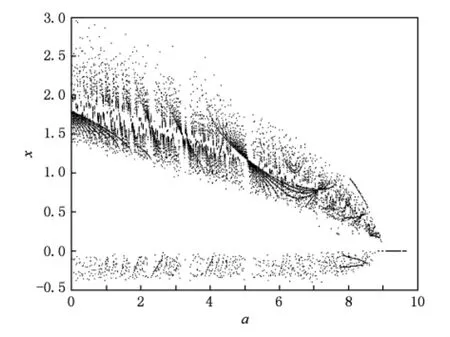
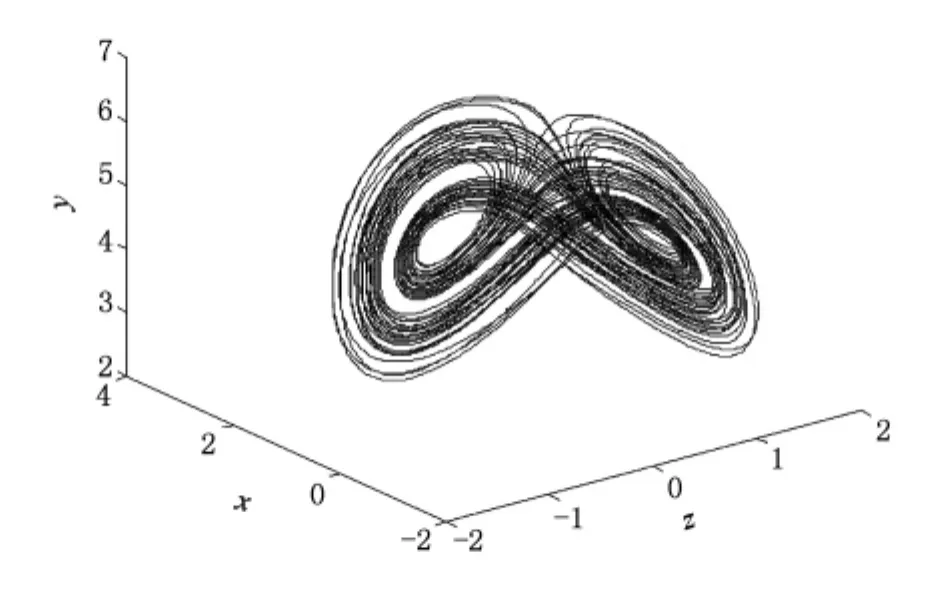
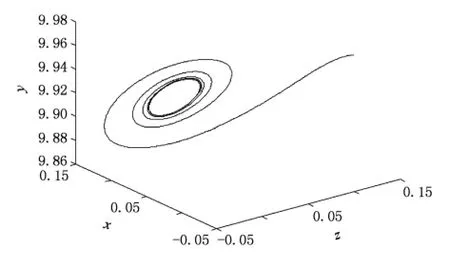
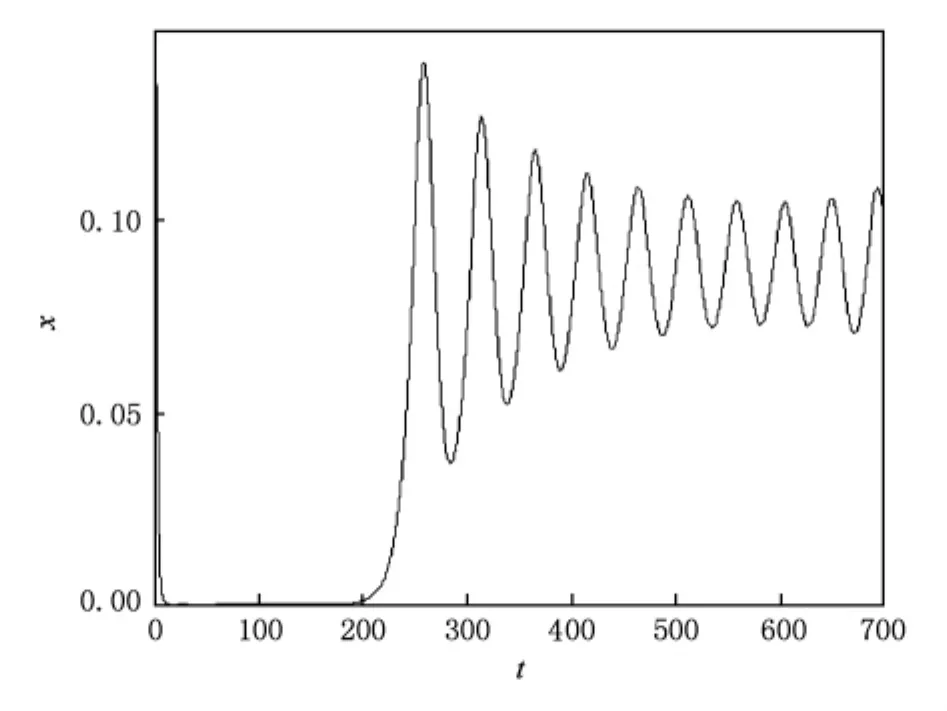
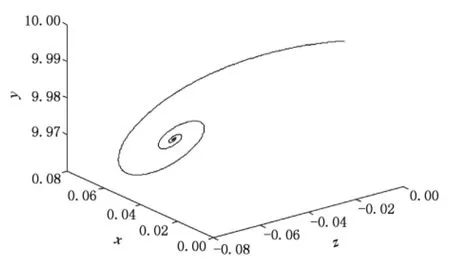
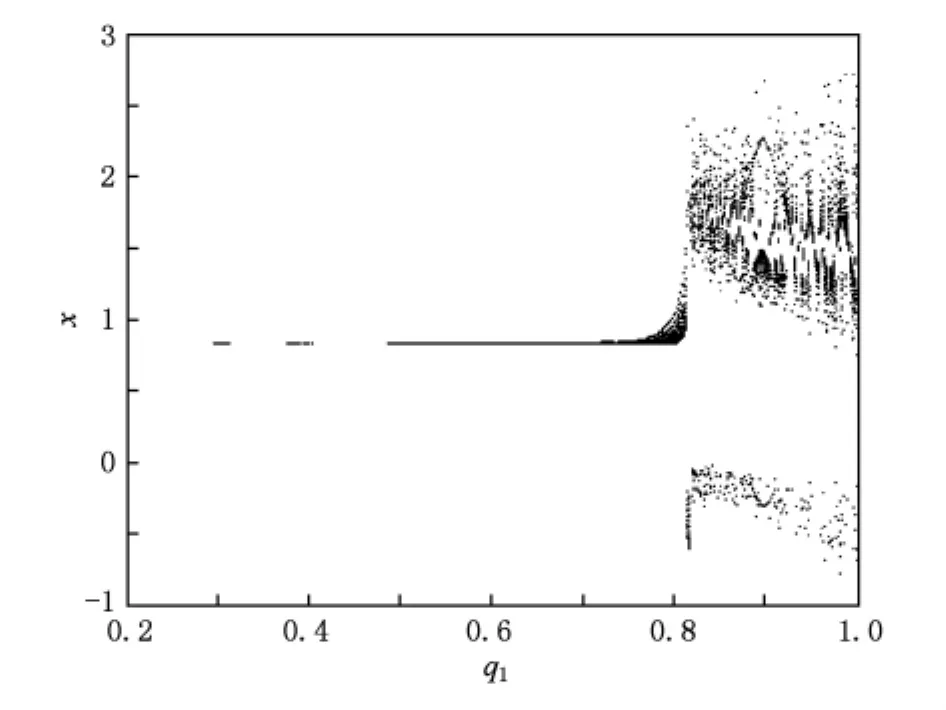
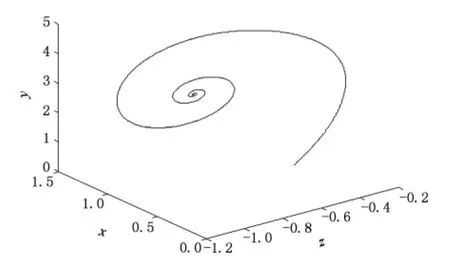
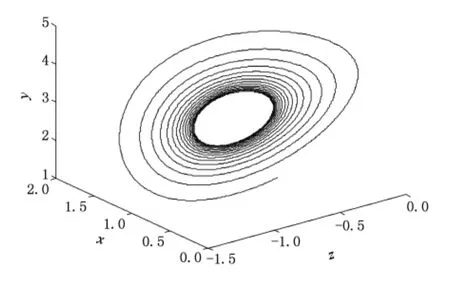
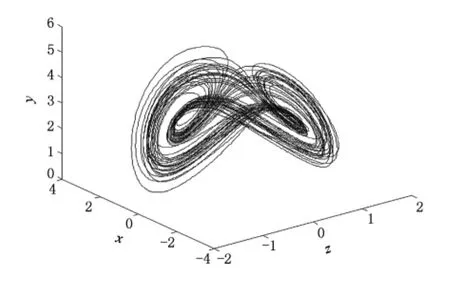
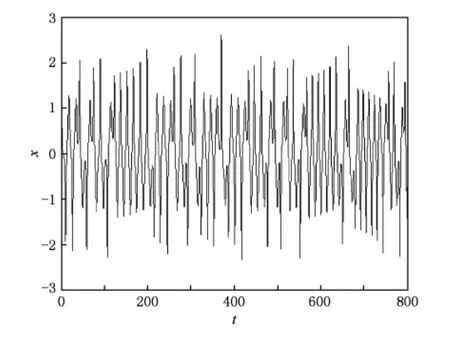
其中 0 Chen[16]通过数值模拟的方式研究了系统(2)的混沌吸引子等复杂动力学现象.本文将在该文献的基础上,定性分析系统(2)的稳定性和Hopf分岔产生的条件,并运用亚当斯-巴什福斯-莫尔顿预估-校正的有限差分法[26,27],通过分岔图、相图和时间序列图对该混沌金融系统的复杂性演化路线进行仿真研究. 令 通过求解方程(3),可以得到如下结论: 1)当 c-b-abc≤0,系统(2)有唯一的平衡点 2)当 c-b-abc>0,系统(2)有三个平衡点 的稳定性.系统 其特征方程为 其中一个特征值为λ1=-b<0,另外两个特征值λ2和λ3是由下式决定的: 则E0点会出现以下三种情形: 例 1 当 q1=0.88,q2=0.98 和 q3=0.92,b=0.1和c=1时, 2)对于第2种情形,若a<9,则系统(2)就是不稳定的; 本部分运用亚当斯-巴什福斯-莫尔顿预估-校正有限差分法[26,27],分别模拟储蓄量 a和微分阶数q1的变化对系统(2)复杂性演化的影响. 同例1一样,设定 q1=0.88,q2=0.98和 q3=0.92,b=0.1 和 c=1,另取初值(x0,y0,z0)=(2,3,2).当我们对储蓄量a∈[0,10]调整时,可以画出系统(2)的利率x的分岔图,如图1所示. 图1 系统(2)的利率x随储蓄量a变化的分岔图 分岔图1表明,系统(2)的复杂性随着我们对储蓄量a∈[0,10]的调整而发生相应的变化. 我们可以取储蓄量a=4,则系统(2)的相图如图2所示,利率x的时间序列图如图3所示. 将图2和3与分岔图1结合在一起分析,可以发现该经济金融系统的变化比较剧烈,正处于混沌状态,无法对该系统的未来状态进行长期预测,整个系统处于一种失控状态,会产生非常大的破坏作用,需要及时给予宏观调控,平抑系统的长期剧烈波动. 图2 储蓄量a=4时系统(2)的相图 图3 储蓄量a=4时系统(2)的利率x的时间序列图 我们可以取储蓄量a=9,则系统(2)的相图如图4所示,利率x的时间序列图如图5所示,结合分岔图1,可以发现该系统在 a=9处发生 Hopf分岔,整个系统处于规律的周期性运动变化状态. 我们可以将储蓄量设定为a=9.01,则系统(2)的相图如图6所示,利率x的时间序列图如图7所示.结合分岔图1,我们可以发现当a>9时该系统趋向于稳定均衡状态. 图4 储蓄量a=9时系统(2)的相图 图5 储蓄量a=9时系统(2)的利率x的时间序列图 图6 储蓄量a=9.01时系统(2)的相图 图7 储蓄量a=9.01时系统(2)利率x的时间序列图 总之,0≤a<9时,系统(2)处于不稳定的混沌状态,波动较为剧烈,会对经济稳定运行产生较大的破坏作用,需要适时给予调控,防止经济金融系统的长期剧烈波动;a=9时,系统(2)会发生 Hopf分岔,整个系统处于周期性运动变化状态,但也是一种不稳定的状态;a>9时,系统(2)处于渐近稳定均衡状态,整个经济金融系统能够稳定有序地运转,可以对该系统的未来状态进行长期预测. 设定 q2=0.98,q3=0.92,a=2,b=0.1 和 c=1,取初值(x0,y0,z0)=(2,3,2).当我们对微分阶数q1∈(0,1)调整时,可以画出系统(2)利率 x的分岔图,如图8所示. 图8 系统(2)的利率x随q1变化的分岔图 分岔图8表明,系统(2)的复杂性随着我们对微分阶数q1∈(0,1)调整而发生相应的变化:从稳定状态经过分岔进入混沌状态. 令q1=0.7时,系统(2)的相图如图9所示,利率x的时间序列图如图10所示.结合分岔图8,我们可以发现,当q1<0.8时该系统趋向于稳定均衡状态. 图9 q1=0.7时系统(2)的相图 令q1=0.8时,则系统(2)的相图如图11所示,利率x的时间序列图如图12所示,结合分岔图8,可以发现该系统在q1=0.8处发生分岔,整个系统处于规律的周期运动变化状态. 图10 q1=0.7时系统(2)利率x的时间序列图 图11 q1=0.8时系统(2)的相图 图12 q1=0.8时系统(2)利率x的时间序列图 设定q1=0.9时,则系统(2)的相图如图13所示,利率x的时间序列图如图14所示,结合分岔图8,可以发现该系统正处于混沌状态,需要择时进行宏观调控,防止系统长期剧烈波动. 图13 q1=0.9时系统(2)的相图 图14 q1=0.9时系统(2)利率x的时间序列图 总之,0≤q1<0.8时,系统(2)处于渐近稳定均衡状态,整个系统稳定有序地运转.q1=0.8时,系统(2)会产生分岔,整个系统处于周期性运动变化状态;0.8 经济混沌是经济金融系统中的一种内在不确定性,是经常出现在该系统中的一种极其复杂的现象,是当前非线性经济动力学研究的一项重要内容.本文定性地研究了一类分数阶混沌金融系统的稳定性和Hopf分岔发生的条件,并运用亚当斯-巴什福斯-莫尔顿预估-校正的有限差分法,通过分岔图、相图和时间序列图,分别数值模拟了储蓄量和微分阶数对分数阶金融系统复杂性演化行为的影响,得出了一些有意义的研究结果,可以为政府调控经济金融系统提供理论依据. [1] Arthur W 1994 Am.Econ.Rev.84 406 [2] Challet D,Zhang Y 1997 Phys.A 246 407 [3] Huang Z,Chen Y,Zhang Y,Wang Y 2007 Chin.Phys.16 975 [4] Guo R,Huang H 2008 Chin.Phys.B 17 1698 [5] Chen W D,Xu H,Guo Q 2010 Acta Phys.Sin.59 4514(in Chinese)[陈卫东、徐 华、郭 琦2010物理学报 59 4514] [6] Gou C,Gao F,Chen F 2010 Chin.Phys.B 19 110514 [7] Wang Z,Xu Z,Huang J,Zhang L 2010 Chin.Phys.B 19 100204 [8] Zhou P,Wei L,Cheng X 2009 Chin.Phys.B 18 2674 [9] Zhang R,Yang S 2009 Chin.Phys.B 18 3295 [10] Liu Y,Xie Y 2010 Acta Phys.Sin.59 2147(in Chinese)[刘 勇、谢 勇2010物理学报59 2147] [11] Wang M,Wang X 2010 Acta Phys.Sin.59 1583(in Chinese)[王明军、王兴元2010物理学报 59 1583] [12] Liu D,Yan X M 2010 Acta Phys.Sin.59 3747(in Chinese)[刘 丁、闫晓妹2010物理学报 59 3747] [13] Huang L L 2011 Acta Phys.Sin.60 010505(in Chinese)[黄丽莲2011物理学报 60 010505] [14] Jiang X,Xu M,Qi H 2010 Nonlinear Anal-Real 11 262 [15] Liu Y,Ma J 2009 Commun.Theor.Phys.52 857 [16] Chen W 2008 Chaos,Soliton.Fract.36 1305 [17] Song L,Xu S,Yang J 2010 Commun.Nonlinear Sci.Numer.Simulat.15 616 [18] Ahmad W,El-Khazali R 2007 Chaos,Soliton.Fract.33 1367 [19] Puu T 1997 Nonlinear economic dynamics(NY:Springer Verlag) [20] Xin BG,Ma J,Gao Q 2009 Chaos,Soliton.Fract.42 2425 [21] Sprott J 2003 Chaos and time-series analysis(NY:Oxford Univ.Press) [22] Huang D,Li H Q 1993 Theory and method of the nonlinear economics(Chengdu:Sichuan Univ.Press)(in Chinese)[黄登仕、李后强1993非线性经济学的理论和方法(成都:四川大学出版社)] [23] Qiu T 2010 IMF head:No asset bubble in Asia.In Wen Wei Po(HK:Wen Wei Po Press) [24] Jiang X,Xu M 2010 Phys.A 389 3368 [25] Podlubny I 1999 Fractional differential equations(NY:Academic press). [26] Diethelm K,Ford N,Freed A 2002 Nonlinear Dynam.29 3 [27] Deng W,Li C 2008 Phys.Lett.A 372 401 [28] Hu J B,Han Y,Zhao L D 2009 Acta Phys.Sin.58 4402(in Chinese)[胡建兵、韩 焱、赵灵冬 2010物理学报 58 4402] [29] Deng W 2010 Nonlinear Anal-Theor.72 1768 PACS:89.65.Gh,05.45.- a,02.30.Oz Complexity evolvement of a chaotic fractional-order financial system* Xin Bao-Gui1)2)Chen Tong1)Liu Yan-Qin1)2) A novel science branch,econophysics,is set up because various physical theories and methods are applied to economic and financial fields.More and more researchers are fascinated by the complex dynamical behavior of the fractional-order dynamical system.The paper analyzes the stability of the fractional-order financial system,and then simulates the generalized model complexity with Adams-Bashforth-Moulton predictor-corrector scheme by using bifurcation diagram,phase portrait and history time-series. econophysics,fractional ODEs,finance model,chaos *中国博士后科学基金(批准号:20100470783),高等学校博士学科点专项科研基金(批准号:20090032110031)和国家自然科学基金(批准号:60904063)资助的课题. E-mail:xin@tju.edu.cn *Project supported by the China Postdoctoral Science Foundation(Grant No.20100470783),Specialized Research Fund for Doctoral Program of Higher Education from Ministry of Education of China(Grant No.20090032110031)and National Natural Science Foundation of China(Grant No.60904063). E-mail:xin@tju.edu.cn3.分数阶混沌金融系统的稳定性
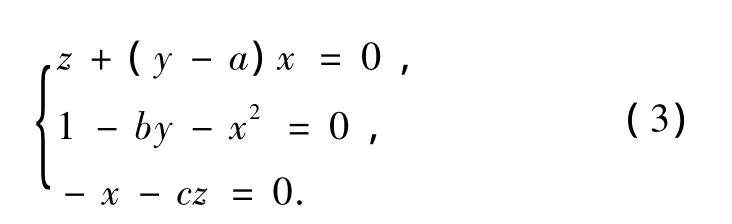




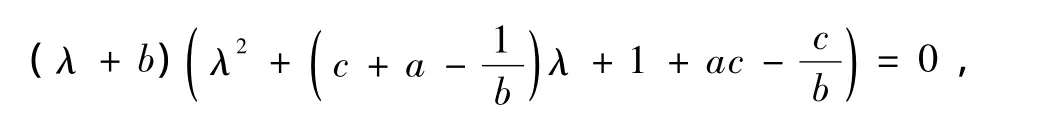
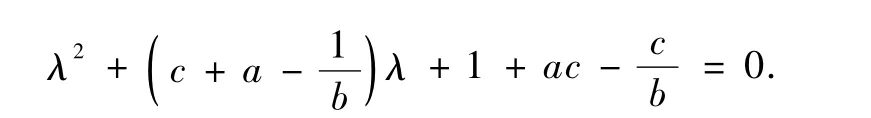
4.分数阶混沌金融系统复杂性演化仿真
4.1.储蓄量a对系统(2)复杂性演化的影响


4.2.微分阶数q1对系统(2)复杂性演化的影响


5.结 论
1)(School of Management,Tianjin University,Tianjin 300072,China)2)(School of Economics and Management,Shandong University of Science and Technology,Qingdao 266510,China)(Received 21 June 2010;revised manuscript received 2 August 2010)
