高强钢轴心受压构件的稳定性研究
2011-10-25张银龙苟明康
张银龙 苟明康 李 宁 梁 川
(1.总装工程兵科研二所,北京 100036;2.总装工程兵科研一所,无锡 214035)
随着钢结构生产、设计研发的不断发展,高强钢结构得到了进一步的发展和应用[1]。但高强钢结构的设计包括稳定性设计有别于普通低碳钢结构。而目前的钢结构设计理论基本都是基于屈服强度相对较低(一般低于450MPa)的结构钢而言的,对屈服应力高于450MPa的结构钢的设计和规定目前还是空白,需要对屈服强度高于450MPa的结构钢进行设计制作时也基本是借用了现行相关设计规范的规定。为此,国内外众多的研究者对高强钢结构及其稳定问题展开了研究。
本文探讨了国内外高强钢结构稳定性计算方法的研究现状和存在的不足,采用大型有限元分析软件ANSYS数值模拟方法和模型试验方法对高强钢箱形截面和工形截面轴心受压构件稳定性进行了探讨,并提出了以材料屈服强度和构件长细比为参数计算高强钢轴心受压构件稳定系数的计算公式。
1 高强钢轴心受压构件稳定性研究现状
几十年来国外高强钢的发展很快。日本、美国、前苏联及欧洲钢结构协会等都对高强钢进行了多方面的研究,但高强钢的柱子曲线研究和高强钢结构的稳定性研究成熟的理论和成果并不是很多。在我国,民用上的应用和研究还很少,主要集中在我军工程装备保障尤其是军用桥梁装备中[2]。
虽然国内外对高强钢进行了不少研究,但专门的高强钢结构的设计理论还不完善,针对高强钢结构的稳定性研究也还很少。因此,在高强钢构件的稳定性设计方面还存在很多不足,主要体现在[3-5]:
1.对于高强钢受压构件中的板件宽厚比限制过严,高强钢的高强性能不能得到真正发挥。
2.有关高强钢构件中整体屈曲和局部屈曲的相关性研究还不充分。
3.研究由板件组成的构件整体屈曲和局部屈曲相关性的问题时,没有考虑各个板件之间的相互嵌固约束作用。
4.考虑构件局部失稳的有效宽度法设计过程复杂,未能充分考虑整体屈曲和局部屈曲的相关性。
5.高强钢构件的稳定性研究的模型试验代价昂贵,数据有限,还不足以提出有关高强钢构件稳定极限承载力的计算公式。
2 高强钢轴心受压构件ANSYS稳定性分析功能
为了弥补高强钢构件稳定性研究模型试验代价昂贵、数据有限的缺陷,可以利用大型有限元分析软件ANSYS的静力分析、特征值屈曲分析和非线性屈曲分析等功能来进行高强钢轴心受压构件整体稳定性研究的有限元数值模拟[6]。其中,静力分析用于求解静力荷载作用下结构的静力行为。特征值屈曲分析用于预测一个理想弹性结构的理论屈曲强度(分叉点),其失稳模态形状可用作非线性屈曲分析的初始几何缺陷。非线性屈曲分析是用一种逐渐增加荷载的非线性静力分析技术来求得使结构开始变得不稳定时的临界荷载的分析方法,模型中可以包括诸如初始缺陷、塑性、间隙及大变形响应等特征。
建立ANSYS有限元分析模型时,材料模型选用多线性等向强化模型。为了考虑板件的局部屈曲和杆件的整体屈曲,分析模型中选用了4节点的壳单元shell181。有限元模型的单元数目根据构件的具体尺寸而略有不同。
有限元模型采用箱形截面和工形截面两种,但没有考虑截面的冷弯效应及倒角。为了模拟刚周边假定,也为了施加约束和荷载的方便,在杆件的两端加上了两块刚性板。考虑采用简支约束,对模型施加约束时,仅需约束两端刚性板中央处的节点即可。基本的ANSYS有限元模型建立完成之后,便可以在此基础上引入初始缺陷和残余应力。
初始缺陷包括局部缺陷和整体缺陷两种。对于局部缺陷是采用一致缺陷模态法,通过进行特征值屈曲分析得到一阶屈曲模态,将此模态乘以一定的系数后引入到原始模型中。而整体缺陷则是在引入局部缺陷之后,将模型的节点位置按照正弦半波形式偏移,根据偏移后的节点重新生成有限元模型。

图1 箱形截面和工形截面的残余应力分布
由于缺乏必要的高强钢焊接构件的残余应力试验数据,对于残余应力选用了如图1所示的模型[7-8],并编制残余应力文件后读入,将残余应力引入到有限元模型中。编制残余应力文件时,将残余应力施加在单元的积分点位置,每个shell181单元选用5个积分点,5个积分点沿板厚均匀分布。假定施加的残余应力在5个积分点上大小相等,即残余应力沿板件厚度方向不发生变化。
基于ANSYS强大的APDL功能,编写了用于计算高强钢箱形截面和工形截面轴心受压构件稳定性计算的ANSYS程序,主要包括基本模型模块、引入缺陷模块、引入残余应力模块、求解模块和后处理模块等5个模块:
1.基本模型模块主要完成构件基本模型的建立,并进行特征值屈曲分析,为以后的分析提供基础。
2.引入缺陷模块主要是引入模型的局部初始缺陷和整体初始缺陷。
3.引入残余应力模块是根据构件残余应力的分布模式、构件的截面及网格划分的具体情况,编制残余应力文件,将其读入到有限元模型中,并逐一施加到相应的单元积分点上。
4.求解模块主要是通过弧长法求解以获得轴心受压构件的荷载系数(即构件的稳定系数)。
5.后处理模块主要是通过提取所关心的节点荷载和位移数据,得到构件或结构的荷载-位移曲线,通过荷载-位移曲线得到结构的极限承载能力,并输出相应的图形或数据。
3 高强钢轴心受压构件ANSYS稳定性分析结果
利用ANSYS的稳定分析功能,对材料屈服强度或名义屈服强度为235MPa、345MPa、590MPa、686MPa、700MPa、745MPa 和 960MPa、长细比在 10~250之间的轴心受压构件的稳定性进行了数值模拟研究,结果发现:
(1)轴心受压构件的稳定系数与材料的弹性模量之间基本成线性关系。不过,如果在一定置信度范围内认为同一批材料的力学性能完全相同,可以采用钢材常用的弹性模量206GPa。
(2)轴心受压构件的稳定系数随着材料屈服强度的增大而减小,同时,稳定系数与按钢结构设计规范GB50017-2003采用等效长细比方法得到的稳定系数之间的误差也随着材料屈服强度的增大而增大,在屈服强度590MPa时两者之间的误差达到最大,随后随着屈服强度的增加这种增大趋势逐渐减缓。由此可以看到,高强钢材料的应用并不意味着对结构稳定性能的绝对提高。所以,对于高强钢材料轴心受压构件的稳定系数仍然采用等效长细比的方法由规范查表插值求得显然不尽合理,也就是钢结构设计规范(GB50017-2003)中给出的轴心受压构件的稳定系数对高强钢构件的适用性存在一定的局限性,需要对高强钢轴心受压构件的稳定系数进行修正。
(3)初始缺陷对轴心受压构件的稳定性存在着一定的影响,在构件长细比50左右时影响最大。对小长细比构件而言,容易发生整体性的全截面屈服,出现局部屈曲的可能性较小;而大长细比构件出现失稳的主要决定因素是长细比,受初始缺陷的影响相对较小;但中等长细比构件可能首先出现局部屈曲,此时初始缺陷的不同会对构件的稳定性产生很大的影响。但在相同构件长细比条件下,轴心受压构件的稳定系数随着初始缺陷的增大而减小。
大长细比构件和小长细比构件对整体初始缺陷的敏感性(在同一构件长细比条件下,轴心受压构件稳定系数随整体初始缺陷变化而变化的范围,变化范围越大说明此类构件长细比对整体初始缺陷敏感性越强,反之表示敏感性越弱)较弱,中等长细比构件对整体初始缺陷的敏感性较强,尤其是长细比在50左右的构件对整体初始缺陷的敏感性最强,在设计中应引起注意。这也是因为是长细比是中等长细比轴心受压构件失稳的主要决定因素。
(4)根据ANSYS稳定性分析数值模拟所得到的计算结果,取正则化长细比 λn=(λ/π)为构件的长细比,fy和E分别为钢材的屈服强度和弹性模量),经过拟合可以得到正则化长细比λn和稳定系数φ的关系函数为
φ =0.913 6+1.327 9λn- 10.712 5λ2n+35.816 5λ3n- 64.960 7λ4n+70.217 2λ5n- 48.695 1λ6n+22.610 3λ7n-7.145 4λ8n+1.522 6λ9n-0.208 7λ10n+2.619 ×
其回归系数和均方差分别为0.994 7和0.024 38[9]。在对原始数据进行回归分析时考虑了95%的置信度。
显然,以材料屈服强度和构件长细比为参数得到的拟合曲线具有较高的回归系数和较小的均方差,拟合曲线的回归模型是可信的,拟合曲线和原始数据点的对比如图2所示。从图中可以看出采用高次曲线拟合得到的曲线与原始数据点吻合较好,并且大部分数据点都略在拟合曲线的上方,说明拟合公式得到的结果略偏于保守,有利于提高构件稳定的安全可靠性。

图2 正则化长细比和稳定系数的关系拟合曲线
4 高强钢轴心受压构件稳定性试验
为了验证关于高强钢轴心受压构件稳定性分析的ANSYS数值模拟计算结果,获得较为可靠的理论计算方法,在总装某研究所结构实验室进行了高强钢轴心受压构件的整体稳定性试验。试件材料BS700,屈服强度700MPa。试件采用16根箱形截面,4根工形截面,截面尺寸(翼缘宽×厚-腹板高×厚)分别为箱形45×3-69×3、36×4-52×4、40×4-52×4、40×4-57×4、工形66×6-88×6,构件长选用600、800、1000、1200(因支座尺寸的影响,实际计算长度略有变化)。支座约束选用单向铰支承。
把高强度钢轴心受压构件竖直置于试验台上,对试件通过油缸施加垂直荷载,以位移法控制荷载的大小,直至构件出现失稳破坏,即试件发生位移突变为止(在计算机控制系统上出现明显的卸载现象)。
针对5组20根轴心受压构件,利用ANSYS数值模拟方法进行了轴心受压构件稳定性分析,得到试件的稳定承载力,求得稳定系数,并与试验结果和拟合公式进行了比较,结果见表1。
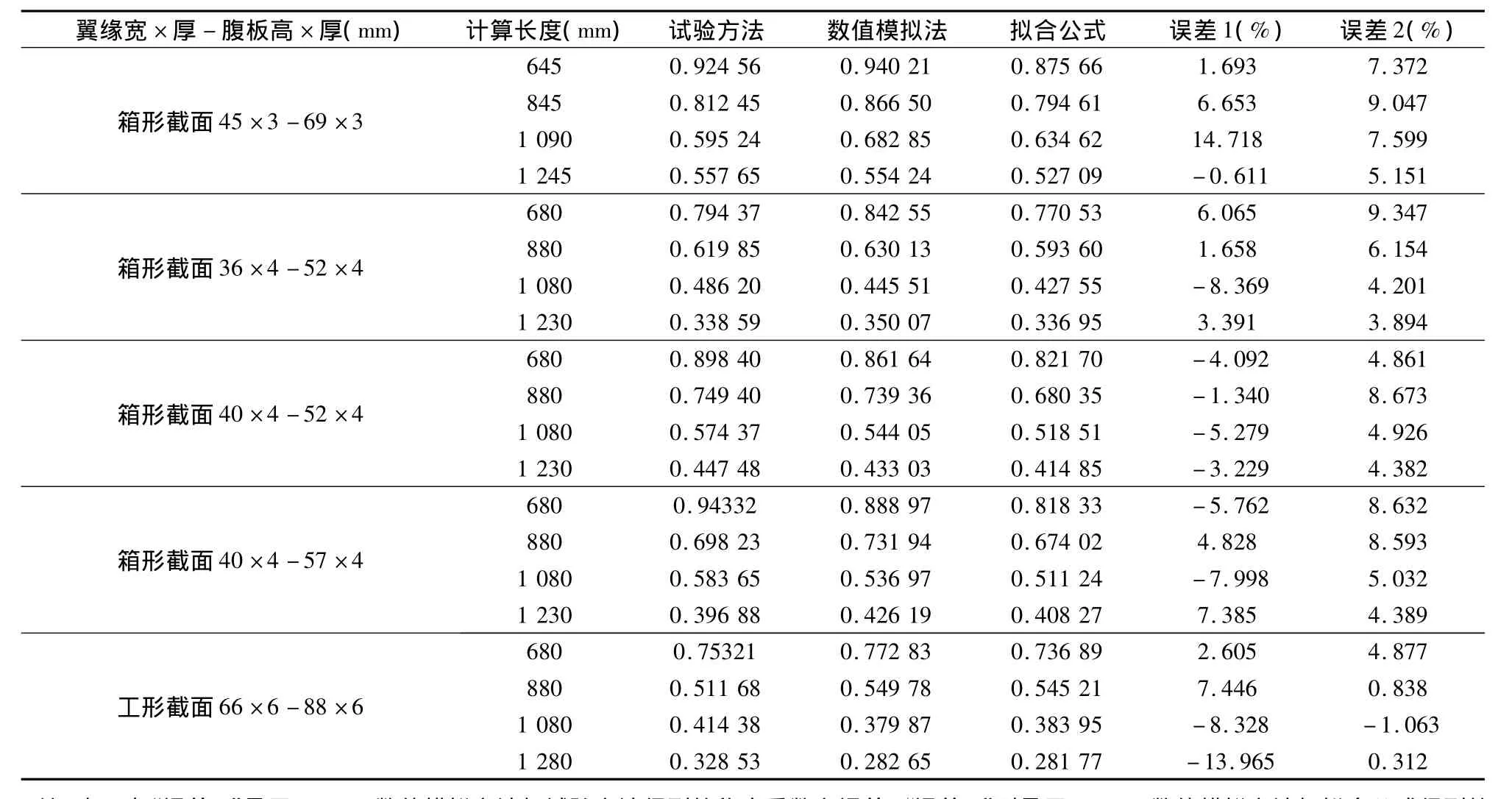
表1 高强钢轴心受压构件稳定系数结果对比
从表1中可以看出,除截面尺寸为45×75、长1 090的箱形截面构件和截面尺寸为翼缘66×6、腹板88×6、长1 280的工形截面构件的理论值与试验值之间的误差较大外,其余构件的理论值与试验值之间的误差均小于9%,虽大于常规的误差限值5%,但对于稳定性研究而言应该说理论值与试验值还是比较吻合的,因为理论计算模型是一种理想化的模型,而试验模型本身、试验过程都存在着一定的不确定因素,而且影响构件稳定性的因素又比较复杂,这些对试验最后的结果都存在着很大的影响;另外,还可以看出,因为拟合公式考虑了95%的置信度,所以按拟合公式得到的稳定系数比数值方法计算的结果要小,而且大多数也比试验结果略小,这再次说明了拟合公式的结果是偏于安全的。因此,研究高强钢轴心受压构件稳定性的ANSYS数值模拟计算程序是正确可信的,拟合公式是合理的,计算结果也是准确的。
5 结束语
基于目前高强钢稳定性研究的现状和存在不足的分析,利用大型有限元分析软件ANSYS的稳定性分析功能以及模型试验方法,对高强钢箱形截面和工形截面轴心受压构件的整体稳定性进行了研究和探讨,提出了以材料屈服强度和构件长细比为参数计算高强钢轴心受压构件稳定性计算公式,并得到了一些有意义的结论,对今后高强钢的应用和研究将具有重要的意义。
[1]Japan Road Association.Spec.for Highway Bridges.Steel Bridges,1996.
[2]苟明康,陶莉.σS≥700MPa的高强钢在移动桥梁装备中的应用.钢结构,2002,17(5):6-8,44.
[3]Rasmussen KJR,Hancock GJ.Plate slenderness limits for high strength steel sections,Journal of Constructional Steel Research,1992,23:73-96.
[4]Miki C,Anami K.Fatigue strength of welded joints made of high strength steels.Progress in Structural Engineering Materials,2001:86-94.
[5]陈骥编著.钢结构稳定理论与设计.北京:科学出版社,2003.
[6]王新敏著.ANSYS工程结构数值分析.北京:人民交通出版社,2007.
[7]沈祖炎,张其林.受压方管钢柱的屈曲后极限承载力.土木工程学报,1991,24(3):15-26.
[8]高磊.高强钢薄壁箱形截面构件相关稳定极限承载力研究.解放军理工大学博士学位论文,2008.
[9]包研科,李娜.数理统计与MATLAB数据处理.沈阳:东 北大学出版社,2008.
