基于电子白板的“指数函数”教学案例

李顺芳

基于电子白板的“指数函数”教学案例

李顺芳

一、教学目标

(1)理解指数函数的概念，能画出指数函数的图像；

(2)能应用指数函数概念解决简单的数学问题；

(3)从图像和解析式的不同角度研究指数函数性质；

(4)培养学生主动学习、合作交流的意识，使学生获得研究函数的规律和方法。

二、教学重点与难点

(1)教学重点：指数函数的概念、图像和性质。

(2)教学难点：对底数的分类，如何由图像、解析式归纳指数函数的性质。

三、教学过程

1.利用电子白板的特点，创设有效的数学情景、提出问题、引入课题

电子白板投出：“某种细胞分裂的示意图”(如图1所示)， 提出问题：这种细胞每过30分钟就由1个分裂成2个，设想经过900分钟(15个小时)后会产生多少个细胞？

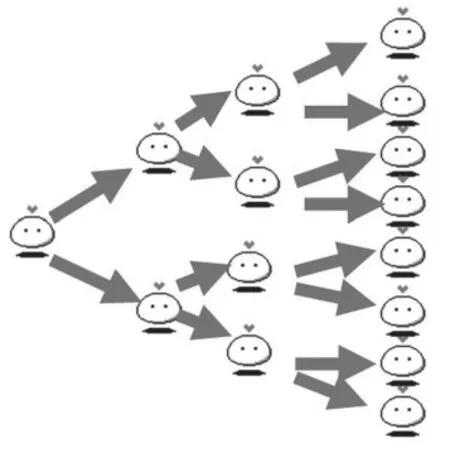
图1

学生回答后，教师在白板上拖动文本框，公布估算的数据：900分钟后细胞总个数10.74亿个。

教师提问：在上面这个问题中，细胞个数用y表示，分裂的次数用x表示，y与x之间的关系是什么？

学生得出公式y=2x( x∈N*)

问：如果经过990分钟(16.5小时)后细胞总数是多少？

师生用白板计算：990分钟后细胞总个数85.90亿个。

教师：y=2x就是我们今天要学习的指数函数。

设计意图：利用白板创设问题情境，引出课题—指数函数，让学生体验从简单到复杂，从特殊到一般的认知规律，激发学生学习新知的兴趣和欲望。

2.利用电子白板进行师生互动、探究新知，找出规律

(1)指数函数的定义

教师在电子白板上投影关系式 y=0.84x

叙述：我们在本章开始的学习中，接触到一个与y=2x类似的关系式，y=0.84x。

问题：①y=2x和y=0.84x这两个解析式有什么共同特征？(是指数形式)

②它们能否构成函数？(能)

③它们是否是我们已学过的函数类型？(否)

教师通过上述问题，引导学生观察上述两个函数的共同特点：指出指数函数的表达式的特点，指数是自变量。用字母a代替底数，上述两式可以表示成y=ax的形式。称作指数函数。

设计意图：人天生有模仿和尝试的欲望，学生此前已经学过一次函数、反比例函数、二次函数，这时用白板创设一个看似认识，但又不同的函数，引导学生从具体问题、实际问题中抽象出数学模型，在具体问题中抽象出共性，激发学生的学习兴趣，建立概念。

(2)指数函数中底数的分类

问题：在指数函数中，底数可以为下列3类吗？

①a＜0

②a=0

③a=1

你能写出上述3种情况下的指数函数形式吗？

学生上台在电子白板上书写几个符合上述条件的指数函数形式。

教师引导学生分析上述底数与指数之间的关系，说明一般情况下不研究这3种情况的指数函数。本课我们主要研究当a＞0且a≠1时的指数函数的性质。

问学生： y＝2×3x是指数函数吗？

教师分析：有些函数式貌似指数函数，实际上却不是，如 y＝ax+k(a＞0且a≠1，k∈Z)；有些函数看起来不像指数函数，实际上却是，如y=a-x(a＞0，且a≠1)，因为它可以化为 y＝(a-1)x，其中a-1＞0，且a-1≠1。

例题讲解：下列函数为指数函数的有 ② ③ 。

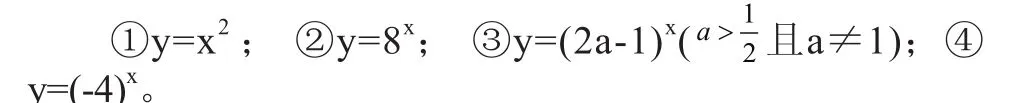
学生在白板上用拖动的方式，将②，③2个正确答案的序号拖到填空线上。

设计意图：底数的分类是本节课的难点，只有认识清楚底数a的特殊规定，才能理解指数函数的定义域；并为后续学习打好基础。让学生通过白板写出三种情况下的指数函数形式，然后指出问题，可使学生加深印象，再通过练习强化概念的理解和应用。

(3)指数函数的图像和性质

教师在电子白板上投影(见表1)：

表1 分析y＝ax的图像和性质

请学生分成小组讨论，完成上表中的图象和解析式。

学生活动：分成两组，一组讨论指数函数的解析式，另一组研究指数函数的图像；然后进行交流。

交流、总结：教师在电子白板上用几何画板软件，改变参数a的值，追踪y＝ax的图像，让学生在图像的变化过程中，观察图像的变化规律和指数函数的性质。

师生共同总结指数函数的图像和性质，教师边总结边在电子白板上分步显示表1的图像和解析式(见表2)。

表2 分析y＝ax的图像和性质

设计意图：通过学生的自主探索、合作学习，变被动为主动，学生成为学习的主人，让学习过程成为一种自觉的行动，从而加深学生对指数函数图像和性质的理解、记忆。

3.应用典型例题理解概念

(1)练习：在同一平面直角坐标系中画出y=3x和y=(1/3)x的大致图像，并说出这2个函数的性质；

(2)例1：已知指数函数f(x)=ax的图像经过点(3,27)，求f(0)，f(1)，f(-3) 的值。

(3)例 2： 比较下列各题中两个值的大小。

①1.82.5，1.83.2；②0.61.2，0.6-1.2；③1.50.6，0.61.5。

根据本题，你能说出确定一个指数函数需要什么条件吗？

教师用电子白板讲解、画图、板书，与学生互动交流、小结。

设计意图：例题设计围绕所学的内容，引导学生理清思路，在熟悉指数函数单调性的基础上学会构造指数函数方法，利用单调性比较两个幂的大小。解题后及时引导学生进行小结，总结在数学活动中所获取的数学经验，领悟数形结合的数学思想方法。

4.巩固训练提升总结

(1)若函数y =(a－1)x在R 上为减函数，则a的范围为

(2)已知下列不等式，比较m，n 的大小。

① am＜an( 1＞a＞0)；

② am＞an( a＞1 )；

③ m=a2.5，n=a3(a＞0，a≠1 )。

设计意图：检查教学目标是否达成，对学生出现的错误，师生及时用白板进行纠正。

四、教学反思

本节课的设计力求能体现新课程的教学理念，采用如下教学模式：创设情境→学生活动→意义建构→形成概念→知识运用→回顾反思。

利用白板工具，改变教学方法，创设情境，从不同的角度理解指数函数，通过对比总结得到指数函数的性质，让学生体会研究方法。

白板的使用，增强了课堂教学的交互性，操作性，学生在动手操作的过程中学习知识，形成概念，探究方法，反馈练习，提高了教学的有效性。

[1] 叶文俊. 电子白板在数学教学中的应用[J].中国信息技术教育，2011，8

[2] 曹远.会当凌绝顶 一览众山小—幂函数的图像与性质(二)白板教学案例[J].中国现代教育装备，2010，6

李顺芳，本科，中教一级。

江苏省南京市田家炳高级中学。

全国教育科学规划专项课题《在科技教育中培养高中生科学素养的策略研究》阶段研究成果之一(编号：GHB093215)。