压缩真空中的电磁诱导透明*

吕纯海 谭 磊2)† 谭文婷

1)(兰州大学理论物理研究所，兰州 730000)

2)(兰州大学磁学与磁性材料教育部重点实验室，兰州 730000)

(2010年2月3日收到;2010年5月5日收到修改稿)

压缩真空中的电磁诱导透明*

吕纯海1)谭 磊1)2)†谭文婷1)

1)(兰州大学理论物理研究所，兰州 730000)

2)(兰州大学磁学与磁性材料教育部重点实验室，兰州 730000)

(2010年2月3日收到;2010年5月5日收到修改稿)

从主方程出发，通过解析求解密度矩阵非对角元，研究了压缩真空中Λ型三能级原子的电磁诱导透明现象(EIT).研究结果表明:EIT显著地依赖于相干光场的相位、压缩真空的压缩强度和压缩相位.Λ型三能级原子不但有电磁诱导透明和慢光速现象，而且还会表现出对探测光的增益、快光速和反向光速效应;且Λ型三能级原子对探测光场的吸收和增益与探测光强度有关，这与普通真空中不同.

压缩真空，电磁诱导透明，增益

PACS:42.50.Nn，42.65.－ k，32.80.Qk

1.引 言

电磁诱导透明(EIT)是一种由原子能级跃迁的相干相消所引起的非线性效应.自它由理论［1］提出并在实验［2］上成功验证以来，便成为研究光与物质相互作用的重要课题［3—5］，比如光速的调控、信息的储存［6—8］以及激光物理［9］等.在近 20年的发展过程中，人们已经在各种介质［10—12］和波段［13］下探索了 EIT的效应，并把原子系统从典型的三能级［1，14，15］推广 到了四能级［16—18］、五能级［19］等情况，并发现了一些新的效应.最近，关于电磁诱导透明中的孤子行为也有报道［20］.但在这些研究中，原子系统所处的环境都只是热库场或普通真空，对于系统所处的环境是压缩库场的情况，尚未见文献报道.

由于压缩光场的双光子关联［21］，使得其相对于热光场、相干态光场在其中一个正交分量上有较小的不确定度，在另一个正交分量上，则表现出比相干态光场和热光场较大的不确定度.这使得压缩光在精确测量［22］(引力波的测量)和提高通信中信号的信噪比［23］方面有着很大的应用.同时，压缩光场与原子的相互作用，也会表现出特有的性质.Gardiner［24］的研究发现，压缩真空中的二能级原子相位的衰减，在其中一正交分量上会受到抑制，而在另 一 正 交 分 量 上 则 会 加 强.Ritsch 等［25］和Carm ichael等［26］在研究压缩真空中二能级原子共振吸收时，发现了探测光吸收光谱的线宽小于普通真空的情况.在国内，关于压缩真空对原子的激光冷却［27，28］和量子纠缠［29—33］等的影响也做了一定研究.日本 Akamatsu 等［34，35］实现了以压缩真空作为探测光场的EIT，并观察到了相应的慢光速效应.然而，理论上对压缩真空中原子系统EIT还未有深入的研究.

基于此，本文将研究压缩真空中Λ型三能级原子的EIT及其相关现象.考虑两个统计独立的宽带压缩真空［36］，从 Born-Markov 近似下［37，38］给出的主方程［39］出发，通过解析求解系统稳态时的密度矩阵元，利用数值和图示法分析体系中各种参数对EIT的影响.研究结果表明:在压缩真空中，原子既可能有一般的EIT和慢光速现象，同时还会出现对探测光场的增益、快光速以及反向光速效应.另外，原子对探测光场的吸收和增益会受到探测光强度的影响.对比在实验上降低光的群速度的机制发现，背景场为压缩真空时其能力要远远高于普通真空时的情形.

2.模型及其求解

考虑一个 Λ型三能级原子，一束弱探测光场Ep，ωp与原子的能级间电偶极矩耦合，失谐为Δ1;然后用另一束强控制光场Ec，ωc与原子能级间电偶极矩耦合，失谐为Δ2(图1).整个系统处于两个统计独立的宽带压缩真空中［36］，其中心频率分别与原子两个跃迁能级近共振.在SchrÖdinger绘景中哈密顿量为

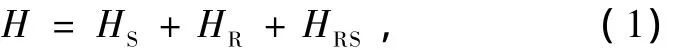
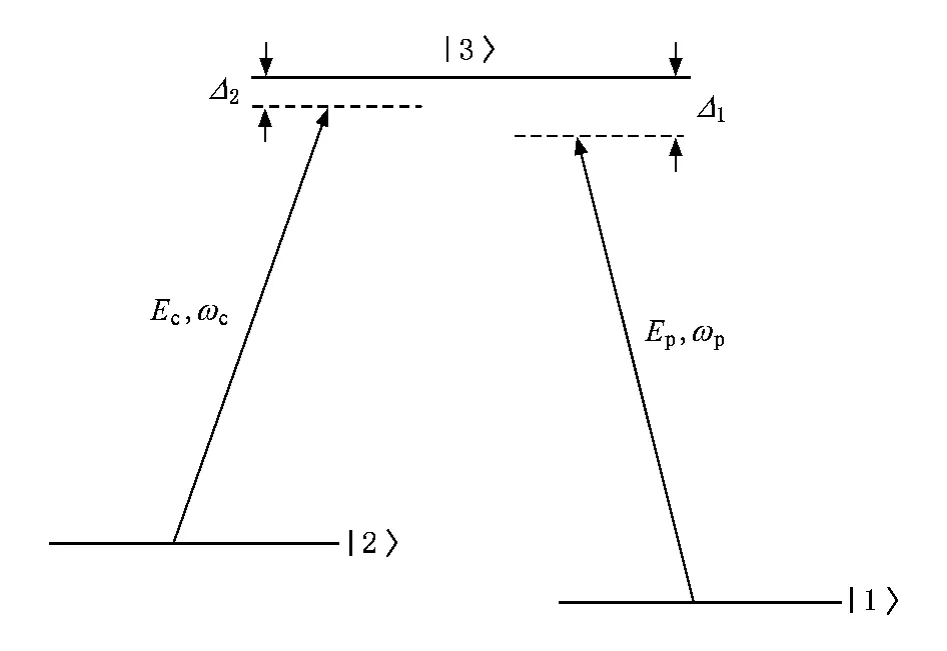
图1 Λ型三能级原子

其中，HS=HA+HI为原子与相干光场系统的哈密顿量.

在旋波近似下，原子与相干光场相互作用哈密顿量为

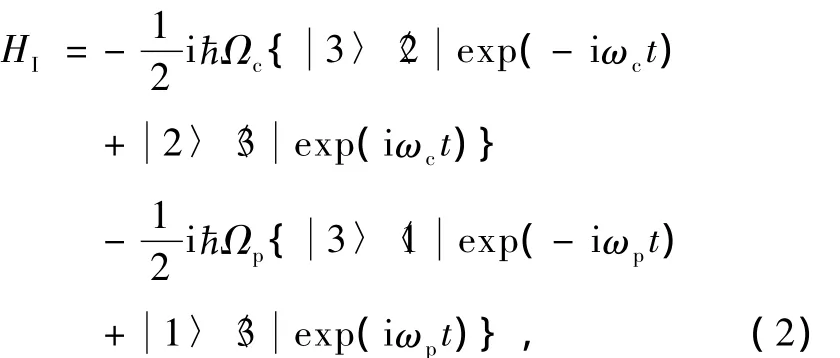
HR为压缩真空的哈密顿量［37］，

HRS表示原子与压缩真空的相互作用哈密顿量，

在 Born-Markov 近 似 下［37，38］，可 以 导 出SchrÖdinger绘景下密度矩阵算符的主方程［39］

其中，非对角矩阵元 ρ31，ρ32，ρ21及其共轭已经取成其缓变函数的形式［3，5］

并且 Ωc，Ωp，Δ1，Δ2，t都对 Γ 做了约化.M前面取正号时表示相位φ=2φL－φs=0，取负号时表示相位 φ=2φL－φs=π，φL和 φs分别代表相干光场(探测光和控制光)的相位和压缩真空的压缩相位.

从Bloch方程(8)可以看出，由于压缩真空与原子的相互作用，密度矩阵元 ρ31，ρ13之间以及 ρ32，ρ23之间出现了直接耦合，而且还与相位φ有关.当M=0时，这种耦合消失，只是通过和的微分方程间接耦合起来.为了便于讨论问题，假设每一个压缩真空的中心频率都与相应光场的频率相同，即ωs1－ωp=0，ωs2－ωc=0，则 Bloch方程(8)存在稳态解.在计算中，假设Δ2=0，并记Δ1为Δ.在此，我们认为第一个压缩真空的中心频率ωs1随探测光场频率ωp一起变化在实验上是可行的.因为 Akamatsu 等［34，35］已经实现了压缩真空作为探测光的EIT实验，那么同时调谐第一个压缩真空中心频率和另一束相干的探测光场也是可行的.当没有探测光，只有强控制光场时，由于自发辐射的影响，稳态时原子的布居将会全部转移到基态能级上，此时 ρ32=ρ23=0;在压缩真空中，这一结果仍然成立，其详细讨论可以参考文献［36］.在EIT中，探测光的强度很弱，一般比控制光强度小 2—4 个数量级［2，11，34，35］，它对原子布居数几乎没有影响，因此我们可以作近似ρ11=1，ρ22=ρ33=0.在这种近似下，的微分方程组可近似取为:

因此，若EIT系统所处的环境为普通真空，密度矩阵元 ρ31，ρ13之间以及 ρ32，ρ23之间没有耦合;若是压缩真空，则将会通过M直接耦合起来.在二能级原子自发辐射中［24］，正是由于这种直接耦合，导致了原子极化的两个正交分量以不同的速率衰减:其中一个分量的衰减被抑制，而另一个则被加强.同样，在本文里，这种直接耦合将极大地改变EIT的性质，并出现一些新的效应.在Bloch方程(8)中取便可求得密度矩阵元的稳态解

其中

式中M前取正号时表示相位φ=0，取负号时表示相位 φ=π .由关系 μ31NAρ31=ε0χEp，其中NA为原子数密度(简便起见，令，可以得到原子介质中线性极化率χ=χ′+iχ″的实部和虚部分别为

当M=N=0时，(11)式化简为

这与普通真空结果相同.对比(13)和(14)式可以看出，压缩真空中原子极化率与相位 φ、压缩真空的压缩强度M以及探测光Rabi频率Ωp有关.由于χ′和χ″分别对应着原子对探测光的色散和吸收，考虑χ′和χ″的性质，即可对色散和吸收的性质作分析.群速度由公式

给出，分析χ′随失谐Δ的变化趋势，便可以定性地给出群速度的性质

在(14)式中，极化率随失谐的函数关系只有一个可调参数，控制光拉比频率Ωc;而在引入压缩真空后的(13)式，可调参数又增加了相位 φ、压缩真空的压缩强度M、平均光子数N以及探测光的拉比频率Ωp，其中相位φ=2φL－φs可以通过调节相干光场相位φL和压缩真空的压缩相位φs得到.因此，在压缩真空情况下，EIT的可调参数更多，其物理效应也就更丰富.

3.压缩真空中EIT和增益

首先，我们研究压缩真空中控制光强度对EIT的影响.图2表示在不同控制光Rabi频率下(Ωc=0.5，5，10)，极化率两分量随失谐Δ的变化，其中相位φ=π.可以看出，控制光越强，EIT的线宽越大.而且对应的吸收曲线呈现出Autler-Townes双峰.因为N≪1，所以吸收峰的线宽即为普通真空中原子自发辐射所造成的自然线宽.这可以从缀饰态理论解释，当强控制光与能级间电偶极矩耦合时，会使得原子能级发生Rabi分裂，在共振时其能级分裂的大小即为控制光 Rabi频率 Ωc的大小，这也正和图中所显示的Autler-Townes双峰的间距所对应.另外，从色散曲线可以看出，控制光强度，χ′越大 共振附近 随失谐的变化率，越大光的群速度也就越慢.因此，在压缩真空中同样可以实现慢光速，达到对光速的控制.所有这些现象都与普通真空中的现象类似［1，3］.

但是，由于双光子关联造成(8)式中矩阵元的直接耦合，压缩真空中的EIT还有其他更丰富的物理效应.下面我们对压缩真空与普通真空的EIT现象作一对比.图3是在同一组探测光和控制光参数下，针对压缩真空N=M=0.002(图3(a)，(b))和普通真空M=N=0(图3(c)，(d))，各自极化率随失谐Δ的变化曲线，其中相位φ=π.从图中可以看出，压缩真空并不会改变EIT窗口的大小和Autler-Townes双峰的位置.这是因为，压缩真空的存在，主要影响原子的极化效应;而对于三能级原子来说，EIT的各种现象来源于原子两个跃迁途径之间的相干相消，主要受控制光 Rabi频率的调制.两种真空情况下的控制光参数一致，那么其表现出来的EIT窗口以及缀饰态的Autler-Townes双峰，也就自然相同.但是从极化率的变化范围来看，压缩真空中的极化率的数值要比普通真空大3个数量级(图3(b)和(d)所示)，在同样条件下，压缩真空中吸收峰的高度是普通真空的近1600倍，原子对探测光的吸收远大于普通真空情形;同时，对比图3(a)(c)，和 的色散曲线 压缩真空中的也比普通真空大近1600倍，在压缩真空中实现对光的群速度的控制，其能力要远远大于普通真空.到目前为止，通过实验EIT效应已经成功地把光的群速度降低到17 m/s［12］.如果我们把背景场换为压缩真空，在其他参数保持不变的情况下，对比图3(a)和(c)的数值结果可以看出，压缩真空中光的群速度可以降低到1.1 cm/s(17/1600 m/s)或更低，大大提高对光的群速度的控制能力.这对拓展EIT在光的群速度调控和量子信息储存方面的应用研究有很大帮助.

图3 不同真空下的 EIT (a)，(b)为压缩真空 N=M=0.002，φ =π;(c)，(d)为普通真空 M=N=0(Ωp=0.0001，Ωc=4.Ωc，Ωp，Δ 均以普通真空中自发辐射速率 Γ 为单位)

图4给出的是相位φφπ时，EIT曲线在不同探测光强度下 (Ωp=0.0002，0.00015，0.0001)的性质.当系统的环境由普通真空换为压缩真空后，极化率两分量随探测光Rabi频率增大而减小.从曲线的演变可以看出，慢光速和吸收峰的高度都对探测光Rabi频率Ωp的变化极其敏感.EIT的这些相关效应受到探测光本身强度(Rabi频率大小)的调制，在普通真空中是不会出现的，为压缩真空所特有.对比(13)和(14)式，正因为压缩真空的存在，M=N=0.002，Bloch方程(8)式中原子密度矩阵元之间出现耦合，极化率才与探测光强度有关.而当M=N=0时，回到普通真空，即(14)式，极化率完全独立于探测光光强.在同样的控制光强度下(Ωc=4)，对于普通真空情况，原子介质对探测光的吸收系数不大于0.5(图3(d));而在压缩真空中(图3(b))，其最大值接近800.由图4(b)中吸收峰随Ωp的变化规律可知，通过适当调节探测光的强度，其吸收峰的高度还会更大.这使得压缩真空中的EIT窗口更加明显.除此之外，压缩真空的压缩强度 M的变化同样会对EIT产生影响.从图5显示的是在不同压缩强度下 (M=0.001，0.0015，0.002)，极化率随失谐Δ的函数曲线，其中相位φ=π.从图5中可以看出，压缩强度越大，原子对探测光的吸收越强(图5(b));同时，探测光场在共振附近的色散性质，即探测光的群速度也极大地依赖于M的取值(图5(a)).其效应类似于探测光强度的影响.

图4 不同探测光强度下的EIT (N=M=0.002，Ωc=2，相位φ=π.Ωc，Ωp，Δ均以普通真空中自发辐射速率Γ 为单位)(a)χ′—Δ 图，(b)χ″—Δ 图

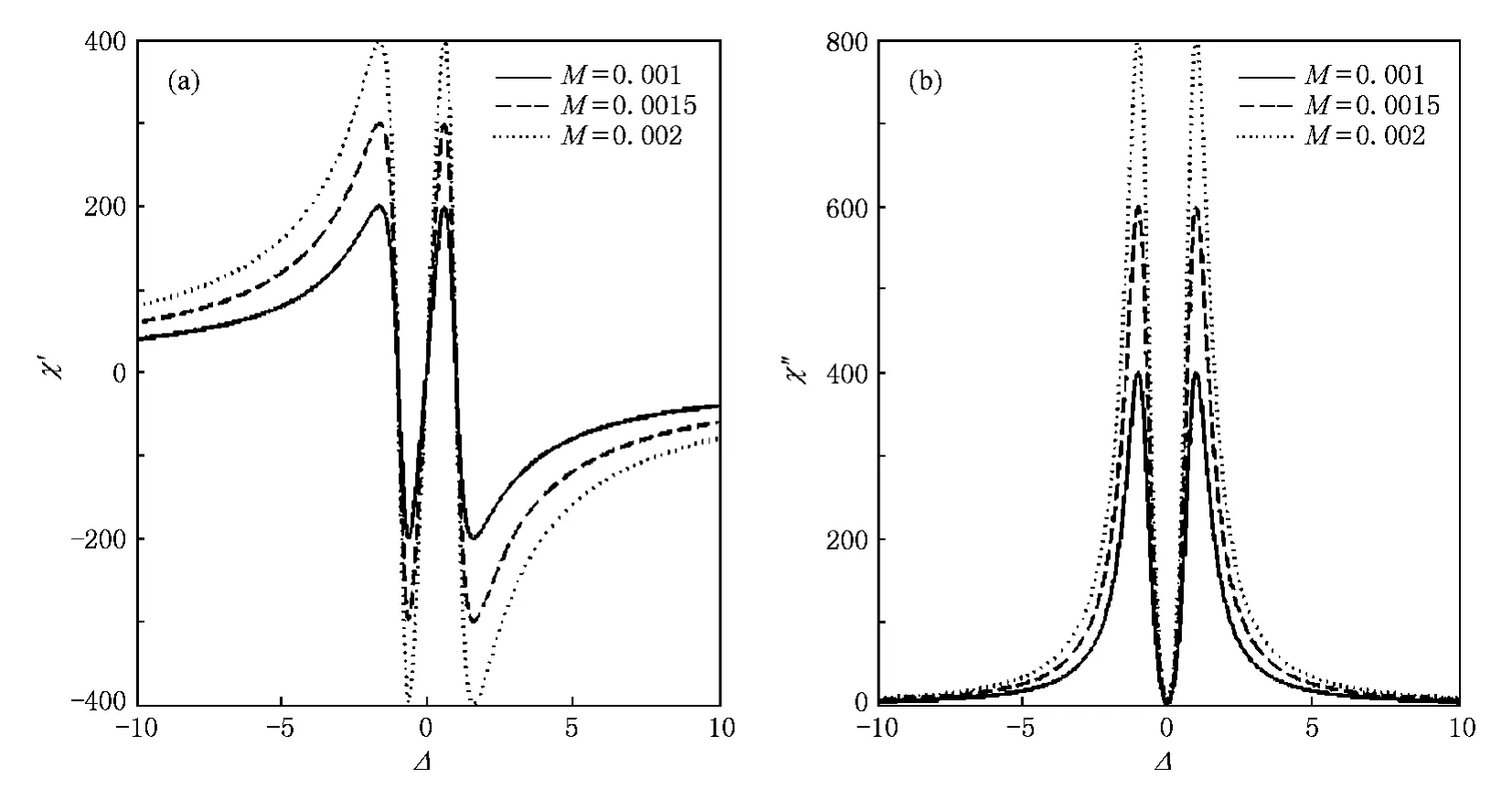
图5 不同压缩强度下的EIT (Ωp=0.0001，Ωc=2，N=0.002，φ =π.Ωc，Ωp，Δ 均以普通真空中自发辐射速率Γ 为单位)(a)χ′—Δ 图，(b)χ″—Δ 图

不同相位下 (φφ=0，π)极化率随失谐 Δ的变化如图6所示.相干光相位和压缩真空的压缩相位将直接影响到EIT与探测光增益(吸收系数 χ″<0)之间的转变(图6(b)).当φφ=0时，对应的吸收系数则会反转，变为负值.也就是说，探测光场在原子介质中不但不会被吸收，相反，还会被增益.由图6(a)中χ′的变化趋势可知，探测光的色散的变化率由正变为负，光的群速度将出现反向光速、甚至快光速现象.从而，调节压缩强度和相位，能够实现由慢光到快光，再到反向光速的转换.而且由图6可以看出，两种情况下的极化率图像几乎都有各自关于χ′=0和χ″=0的对称:图6(b)中，在共振附近探测光的增益趋于零，而在原有的Autler-Townes双峰位置，其增益则为最大;在色散性质方面，图6(a)所显示的曲线也关于χ′=0近乎对称.相位φ=2φL－φs由相干光相位φL和压缩真空的压缩相位φs共同决定，调节φL或φs都可以改变φ的取值(0或π).在普通真空中，EIT不会受到探测光场相位的调制.而这里正是由于(8)式中压缩真空双光子关联M的出现，导致压缩真空中EIT或增益受探测光相位的调制，在本文里，即为调节 φL，φs使得 φ 等于 0或π.

图6 IET和增益(相位φ =π对应着EIT(虚线)，φ =0对应着增益(实线) Ωp=0.0001，Ωc=2，N=M=0.001. Ωc，Ωp，Δ 均以普通真空中自发辐射速率 Γ 为单位)(a)χ′—Δ 图，(b)χ″—Δ 图

如图7所示，当φ=0时，光的群速度以及增益都会受到其他参数的调制.其中图7(a)，(c)分别为色散性质随探测光强度和压缩强度的变化，据此可以对探测光的群速度做定性分析.图7(a)中Rabi，7(c)随探测光 频率增大而增大 图 中.随压缩真空压缩强度增大而减小 由于此，群速度可以是反向光速或快光速增大探测光的强度或减小压缩真空压缩强度，便能实现群速度由反向光速到快光速的转变.探测光的这种增益、反向光速和快光速效应，对于普通真空情况也有可能出现，例如Λ型中原子电偶极矩为负值［40］，或者原子能级为 V 型［14，15］的情形.但是，它们的机理并不相同.文献［40］中是由于电偶极矩μ31为负值，由关系式 μ31NAρ31=ε0χEp可知 χ的符号必定取反，从而表现出上述效应;在V型三能级原子中，此类效应是由于两个激发能级有大的布居所引起的［14］;在本文里，则是由于压缩真空的双光子关联造成原子的两个不同跃迁分量的耦合所致.而且，前两种情况下的这些效应并不会与探测光的强度和相位有关，这也是压缩真空中与普通真空之间最大的区别.

上面的结果并不难理解.因为对于给定的M，N和Ωc，当ΩP≪1时，极化率可以简化为:由于在压缩真空中M和N都较小，K1，K2可以近似

图7 相位φ=0时，原子介质对探测光的色散和增益 (a)，(b)为不同探测光强度下的χ′，χ″—Δ图，其他参量分别为:N=M=0.002，Ωc=4;(c)，(d)为不同压缩强度下 χ′，χ″—Δ 图，其中 Ωp=0.0001，Ωc=4，N=0.002 (Ωc，Ωp，Δ均以普通真空中自发辐射速率Γ为单位)

另外，在上面的分析中平均光子数N很小，由使得(13)式中得以成立，从而图8可知，当平均光子数N增大时，对极化率的影响也很明显，这与(16)式的结果相符.因此，压缩真空的平均光子数 N，也可以明显地对探测光的吸收、增益以及群速度进行调制.最后，必须指出，上面针对(15)式的讨论需要在合适的平均光子数N下才有意义.因为本文中探测光 Rabi频率 ΩP≈10－4，并非无穷小量，所以在压缩真空为最大压缩强度M=N(N+1)下，平均光子数应该满足N≫ΩP得到(16)式，使得上述基于(16)式的定性分析得以成立.

图8 不同平均光子数下探测光的色散和增益 (Ωp=0.0001，Ωc=2，φ=0，对于每一组数据都有M=N，表示压缩真空处于最大压缩强度.Ωc，Ωp，Δ均以普通真空中自发辐射速率 Γ为单位)(a)χ′—Δ图，(b)χ″—Δ图

4.结 论

本文主要研究了Λ型三能级原子在两个统计独立的压缩真空中的EIT现象.在一定的近似下，我们得到了密度矩阵元的解析表达式，并由此可以得到探测光在原子介质中的极化率.实验上，控制光场的强度一般比探测光强度大2—4个数量级，因此这种近似是合理的.由于极化率的实部和虚部分别描述原子介质对光场的色散和吸收性质，因此可以由此分析原子对探测光场传播性质的影响.

从结果可以看出，相对于普通真空来说，压缩真空与原子的相互作用使得探测光在介质中除了具有EIT性质外，还使探测光具有增益、快光速和反向光速的性质.首先，探测光的相位和压缩真空的压缩相位将直接影响到系统的性质:对于φ=0，原子对探测光呈现出增益以及快光速和反向光速的效应;对于φ=π，则是一般的EIT和慢光速效应.其次，在压缩真空中原子对探测光场的吸收、增益和群速度与光场本身的强度有关.另外，EIT的相关效应，受压缩真空的压缩度影响，压缩强度越大，吸收或增益越明显，光的群速度也受到调制.这些效应都是压缩真空与原子之间相互作用性质造成的.相对于普通真空来说，压缩真空中降低光速的能力，要远远高于普通真空.

［1］Harris S E，Field J E，Imamoglu A 1990Phys.Rev.Lett.64 1107

［2］Boller K J，Imamolu A，Harris S E 1991Phys.Rev.Lett.66 2593

［3］Fleischhauer M，Imamoglu A，Marangos J P 2005Rev.Mod.Phys.77 633

［4］Schmidt H，Imamogdlu A 1996Opt.Lett.21 1936

［5］Wang F Y，Shi B S，Lu X S，Guo G C 2008Chin.Phys.B 17 1793

［6］Matsko A B，Kocharovskaya O，Rostovtsev Y，Welch A S Z G R，Scully M O 2001Adv.At.Mol.Opt.Phys.46 191

［7］Fleischhauer M，Lukin M D 2002Phys.Rev.A 65 022314

［8］Eisaman M D，Andre A，Massou F，Fleischhauer M，Zibrov A S，Lukin M D 2001Nature(London)413 273

［9］Bagayev SN，Vasilév V V，Egorov V S，Lebedev V N，Mekhov IB，Moroshkin P V，Fedorov A N，Chekhonin IA 2005Laser Phys.15 975

［10］Xu Q F，Sandhu S，PovinelliM L，Shakya J，Fan SH，Lipson M 2006Phys.Rev.Lett.96 123901

［11］Turukhin A V，Sudarshanam V S，Shahriar M S，Musser J A，Ham B S，Hemmer P R 2001Phys.Rev.Lett.88 023602

［12］Hau L V，Harris S E，Dutton Z，Behroozi C H 1999Nature(London)397 594

［13］Buth C，Santra R，Young L 2007Phys.Rev.Lett.98 253001

［14］Wu Y，Yang X X 2005Phys.Rev.A 71 053806

［15］Li Y Y，Hou X，Bai JT，Yan JF，Gan C L 2008Chin.Phys.B 17 2885

［16］Zhang L S，Li X L，Wang J，Yang L J，Feng X M，Li X W，Fu G S 2008ActaPhys.Sin.57 4921(in Chinese)［张连水、李晓莉、王 健、杨丽君、冯晓敏、李晓苇、傅广生 2008物理学报57 4921］

［17］Zheng J，Liu Z D，Zeng F H，Fang H J 2008ActaPhys.Sin.57 4219(in Chinese)［郑 军、刘正东、曾福华、方慧娟 2008物理学报57 4219］

［18］Du Y J，Ge G K 2008ActaOpt.Sin.28 0375(in Chinese)［杜英杰、葛国库 2008光学学报 28 0375］

［19］Hou B P，Wang S J，Yu W L，Sun W L 2006Phys.Lett.A 352 462

［20］She Y C，Wang D L，Ding JW 2009ActaPhys.Sin.58 3198(in Chinese)［佘彦超、王登龙、丁建文2009物理学报 58 3198］

［21］Walls D F 1983Nature(London)306 141

［22］Grangier P，Slusher R E，Yurke B，LaPorta A 1987Phys.Rev.Lett.59 2153

［23］Saleh B E，Teich M C 1987Phys.Rev.Lett.58 2656

［24］Gardiner CW 1986Phys.Rev.Lett.56 1917

［25］Ritsch H，Zoller P 1987Opt.Commun.64 523

［26］Carmichael H J，Lane A S，Walls D F 1987Phys.Rev.Lett.58 2539

［27］Tan L，Zhang Q，Wang Z C 2005ActaOpt.Sin.25 1277(in Chinese)［谭 磊、张 琴、汪志诚 2005光学学报 25 1277］

［28］Tan L，Zang X F，Li JP，Liu LW，Ding C Y 2008J.Phys.Joc.Jpn.77 044704

［29］Huang Y X，Zhao P Y，Huang X，Zhan M S 2004ActaPhys.Sin.53 0075(in Chinese)［黄燕霞、赵朋义、黄 熙、詹明生2004物理学报 53 0075］

［30］Wen J J，Shao X Q，Jin X R，Zhang S，Yeon K H 2008Chin.Phys.B 17 1618

［31］Wang F Q，Zhang ZM，Liang R S，2009Chin.Phys.B 18 597

［32］Xu X X，Hu L Y，Fan H Y，2009Chin.Phys.B 18 5139

［33］Xiang SH，Shao B，Song K H，2009Chin.Phys.B 18 418

［34］Akamatsu D，Akiba K，Kozuma M 2004Phys.Rev.Lett.92 203602

［35］Akamatsu D，Yokoi Y，Arikawa M，Nagatsuka S，Tanimura T，Furusawa A，Kozuma M 2007Phys.Rev.Lett.99 153602

［36］Joshi A，Puri R P 1992Phys.Rev.A 45 2025

［37］Walls D F， Milburn G J 1995QuantumOptics(Berlin:Springer-Verlag)pp91—97，pp208—210，pp225—227

［38］Louisell W H 1973QuantumStatisticalPropertiesofRadiation(New York:W iley)pp331—368

［39］Ferguson M R，Ficek Z，Dalton B J 1995J.Mod.Opt.42 679

［40］Zhou F X，Niu Y P，Gong S Q 2009J.Chem.Phys.131 034105

PACS:42.50.Nn，42.65.－ k，32.80.Qk

Electromagnetically induced transparency in squeezed vacuum*

Lü Chun-Hai1)Tan Lei1)2)†Tan Wen-Ting1)
1)(Institute of Theoretical Physics，Lanzhou University，Lanzhou 730000，China)
2)(Key Laboratory for Magnetism and Magnetic Materials of Ministry of Education，Lanzhou University，Lanzhou 730000，China)
(Received 3 February 2010;revised manuscript received 5 May 2010)

We studied the electromagnetically induced transparency，where the three-level atom ofΛ-type is put in two statistically independent squeezed vacuums.We start from the master equation containing the decay of the atom to the squeezed vacuums，and solve the non-diagonal densitymatrix element analytically，finding that it is strongly dependent on the squeezing degree and the phase of the squeezed vacuum.There is also a dependence on the intensity and phase of the probe beam，which would not appear in the normal vacuum case.By coup ling with squeezed vacuums，the atom would not only experience electromagnetically induced transparency and slow group velocity，but also induce a fast group velocity，backward group velocity and a gain in the probe light field.Besides，the absorption and gain can be modulated by the intensity of probe light.

squeezed vacuum，electromagnetically induced transparency，light gain

*国家自然科学基金(批准号:10704031)、国家基础科学人才培养基金(批准号:J0630313)、兰州大学理论物理与数学纯基础科学基金(批准号:LZU05001)和甘肃省自然科学基金(批准号:3ZS061-A25-035)资助的课题.

†通讯联系人.E-mail:tanlei@lzu.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant No.10704031)，the National Science Foundation for Fostering Talents in Basic Research of the National Natural Science Foundation of China(Grant No.J0630313)，the Fundamental Research Fund for Physics and Mathematics of Lanzhou University，China(Grant No.LZU05001)，and the Natural Science Foundation of Gansu Province，China(Grant No.3ZS061-A25-035).

†Corresponding author.E-mail:tanlei@lzu.edu.cn