基于核密度估计的图像平滑的最优停止

李 毅, 王远弟

(上海大学理学院,上海 200444)

基于核密度估计的图像平滑的最优停止

李 毅, 王远弟

(上海大学理学院,上海 200444)

运用偏微分方程进行图像平滑的过程中,迭代的最佳停止次数一直都是研究重点.利用随机变量之间的独立性,提出一个基于核密度估计的最优停止准则.该准则能获得准确的最佳停止次数,且不需要预知图像中的噪声水平.数值实验结果表明,该准则所得到的最佳停止次数非常接近于均方差 (mean square error,MSE)方法所得到的最佳停止次数,且适用于多种噪声水平.

偏微分方程;图像平滑;相关系数;核密度估计;最优停止

目前可以通过均方差 (mean square error,MSE)或相关系数[5]来对最佳停止迭代次数作一些判别.本研究基于核密度估计的方法来确定最佳迭代停止次数.数值实验结果表明,本方法确定的迭代停止次数与均方差方法得到的结果非常接近,效果优于文献[5]中的所用方法,并且也适用于多种噪声水平.

1 迭代停止次数的选取

目前,偏微分方程图像平滑的最优停止方法主要有 2大类:一类是必须已知无噪声图像或图像噪声的相关信息,这样获得的最优停止次数就有很高的可信度,因此,这类方法偏重于理论分析,或被用来验证其他方法[6-7];另一类是不需要预知无噪声图像或图像噪声的相关信息,实际应用性较强,比如文献[5]中提出的具有代表性意义的相关系数方法.

下面从扩散方程以及 PM模型入手,研究比较均方差、相关系数和本研究提出的方法.扩散方程为

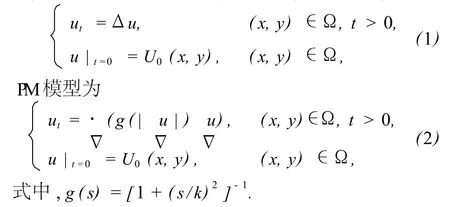
1.1 相关系数

Mrazek等[5]提出的基于相关系数最小时,迭代停止准则的基本思想如下:在图像噪声为加性噪声的前提下,图像被噪声污染的过程可以用 I+n=u0表示,其中 u0代表初始图像,I代表理想的无噪声图像,n代表噪声.扩散滤波过程是从 u0开始获得一系列滤波图像序列 ut的过程.设 ut为 t次迭代获得的滤波图像,此时用 u0-ut近似表示图像噪声,Mrazek等[5]认为最优停止次数应该是在 ut与 u0-ut的相关性最小的时候.其计算式为

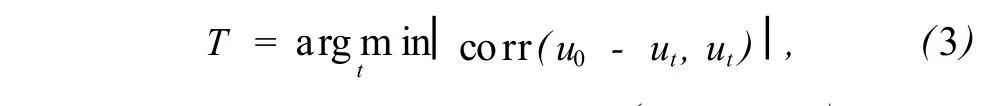
相关系数方法在计算中没有用到无噪声图像或图像噪声的信息,所以其实际应用性较好.但在数值实验中,相关系数方法得到的最优停止次数与均方差方法得到的最优停止次数偏离很多.受相关系数方法的启发,本研究提出一种基于核密度估计的图像平滑最优停止准则.为了验证本方法的可行性与合理性,数值实验将模拟一些已知噪声的图像平滑过程.实验结果表明,本方法得到的最优停止次数非常接近于均方差方法所得到的最优停止次数.一幅图像的信噪比 (signal to noise ratio,SNR)以及最优峰值信噪比 (peak signal to noise ratio,PSNR)的值越大,说明图像的视觉效果越好.因此,在数值实验中,分别计算不同方法在最佳停止时刻所得滤波图像的SNR和 PSNR,结果发现本方法所得滤波图像的SNR以及 PSNR的值要大于相关系数方法所得到的值,可见本方法对滤波图像的最终效果要优于相关系数方法.

1.2 基于核密度估计的图像平滑的最优停止准则

相关系数方法视 ut与 u0-ut为二维随机变量(X,Y),最优停止次数的确定就是围绕二维随机变量 (X,Y)的相关性,找到一个 T,使得此时的 corr(uT,u0-uT)最小.如果二维随机变量 (X,Y)独立,则 corr(uT,u0-uT)=0.为此,本研究提出一个确定迭代停止次数的新准则,记为独立性准则.独立性准则认为二维随机变量 (X,Y)的独立性最大,即相关性最小时的迭代次数为所求结果,可表示为

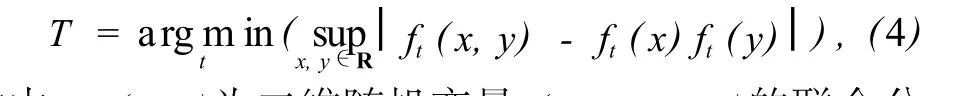
式中,ft(x,y)为二维随机变量 (ut,u0-ut)的联合分布函数,ft(x)与 ft(y)分别为二维随机变量 (ut,u0-ut)的边际分布函数.

1.2.1 理论性质

独立性准则是通过度量二维随机变量 (X,Y)的独立性程度来确定最优迭代停止次数.

设 (Ω,F)为一可测空间,(R,B(R))为数轴及其博雷尔 (Borel)集合系 B(R)上的可测空间.二维随机变量 (X,Y)是独立的,即对于任意的 B1,B2∈B(R),有下式成立

P{X∈B1,Y∈B2}=P{X∈B1}P{Y∈B2}. (5)

若 X=X(ω)为随机变量,考虑 F中形如{ω:X(ω)∈B},B∈B(R)的集合,它们构成由随机变量X生成的σ-代数,记为σ(X).

任意两个σ-代数σ(X)与σ(Y),其独立性度量记为

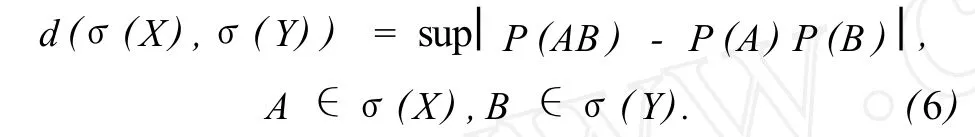
若 σ(X)与 σ(Y)独立 ,则 d(σ(X),σ(Y))=0.

综上,式 (6)可转换为

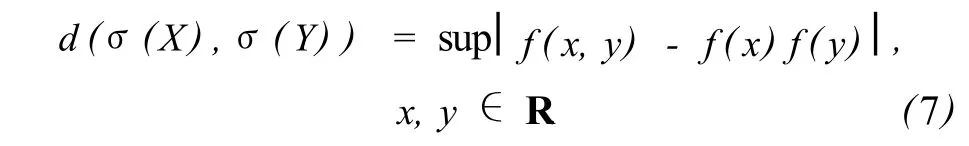
这样,二维随机变量 (X,Y)的独立性程度就可以通过式(7)的值来反映.有关这方面的详细内容可参见文献[8-10].

1.2.2 核密度估计

由式 (4)可知,独立性准则的计算涉及到二维随机变量的联合分布函数和边际分布函数.由给定的数据集估计密度函数,再积分估计分布函数,这个问题是概率统计学中非参数统计的基本问题之一,有关详细情况可参见文献[11],这里仅作简要介绍.

来源于总体的 N个样本点 X1,X2,…,XN,其概率密度函数可以通过下式来估计

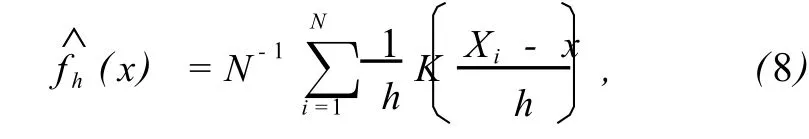
式中,K(·)为核函数,h为窗宽、平滑参数或者核尺寸.

对于二维随机变量 (ut,u0-ut)的联合分布函数和边际分布函数的估计问题,可以先通过下式来估计出概率密度函数,继而积分求其分布函数,即

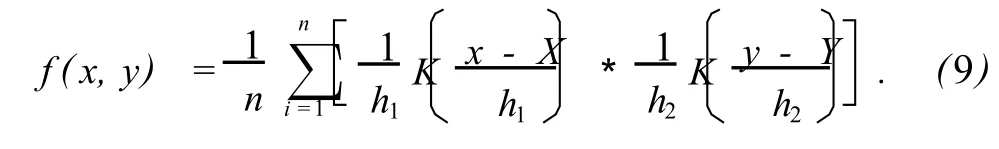
核函数的选择对密度估计来说是不重要的,只要核函数是单峰且对称的即可,因此,选取高斯核不过,密度估计对窗宽的选取十分敏感,大的窗宽会使密度函数曲线过度光滑,而小的窗宽又会使密度函数曲线留有过多震荡[11].为此,本研究采用文献 [11]中介绍的基于数据驱动的窗宽选取算法.

渐近最优窗宽定义为-

但是最优窗宽并不是直接可用的,它涉及到未知的 A(f).在概率统计学的计算中,一般假设 f(x)为具有标准差σ的高斯密度函数.经计算可得,于是可得 ,h＊=(4/3)1/5σN-1/5.

1.2.3 数值实验

本研究将通过一系列的实验来验证独立性准则.二维随机变量 (ut,u0-ut)的取值可看作是二维随机变量的观测样本值.数值实验会涉及到式 (4)中最大值的计算.而求解一个目标函数的最值有很多种方法,本研究的重点不在于最优化方法的讨论,因此本研究利用Matlab中求解无约束最优化的单纯形搜索算法,将初始迭代的值选取为样本值的均值.因为所需要估计的分布函数与样本观测值有关,其最值应该在均值附近,所以设置的迭代搜索的初值为样本观测值的均值.数值实验中采用的图像如图 1所示。

图 2为均方差方法、相关系数方法以及独立性准则随着迭代次数变化的趋势图.所用图像来源于图 1(b),PM模型,SNR的值为 4.744 8,时间步长为0.1.可以看出,3个图形具有类似的走势:开始递减,之后增加.尽管数值实验显示出独立性准则与均方差方法以及相关系数方法有共同点,但还不能从理论上证明最优值存在,所得到的最优停止迭代次数也仅仅是通过实验评估得到的.

图 1 数值实验中采用的图像Fig.1 Images used in the exper im en ts

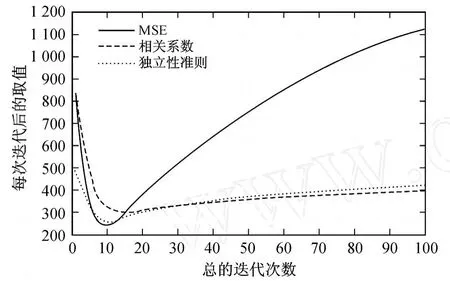
图 2 3种方法随迭代次数变化的趋势图Fig.2 Three methods develop ing w ith the d iffusion time

2 数值结果分析

为了使结果具有可比性,本实验取 SNR的值在0～20范围内的噪声图片.具体地,先对图1(a)所示的图像加入零均值、不同方差的高斯随机噪声,计算出 SNR值,对图 1(b)与图 1(c)所示的图像作同样处理;然后,对加噪声后所得到的一系列噪声图片分别用热传导方程和 PM模型进行平滑去除噪声,同时记录 3种方法在每种方程平滑作用下得到的最佳迭代次数,以及此时刻滤波图像的 SNR和 PSNR的值;最后,画出比较图形.

2.1 不同噪声图片 SNR情况下最佳迭代次数的比较

图 3为不同 SNR的噪声图片用 3种方法所得最佳迭代次数的曲线图.例如,图 1(a)的图像在经过加噪声处理后会得到一系列SNR的值在0～20之间的噪声图片;分别对这些图片用热传导方程和PM模型进行平滑去除噪声,同时记录最佳迭代次数;然后根据噪声图片 SNR的值和最佳迭代次数画出图 3(a)和图 3(b).对图 1(b)和图1(c)所示图像进行类似处理,即可得到图 3(c)和图 3(d)以及图3(e)和图 3(f).

从图 3可以看出,对于不同 SNR的噪声图片,由独立性准则得到的最佳迭代次数都接近于均方差方法得到的最佳迭代次数.而相关系数方法与均方差方法在最佳迭代次数上有偏离,并且在噪声图片SNR值越低,即噪声量越大的时候偏离越大.

2.2 不同噪声图片 SNR情况下最优迭代停止时滤波图像 SNR的比较

图 4为不同 SNR的噪声图片用 3种方法所得到的最优滤波图像 SNR值的曲线图.例如,图 1(a)所示图像在经过加噪声处理后会得到一系列 SNR的值在 0～20之间的噪声图片.分别对这些图片用热传导方程和 PM模型进行平滑去除噪声,同时记录最佳迭代次数以及此时滤波图像的 SNR;然后根据噪声图片和滤波图像 SNR的值画出图 4(a)和图4(b).对图 1(b)和图 1(c)所示图像进行类似处理,即可得到图 4(c)和图 4(d)以及图 4(e)和图 4(f).

从图 4可以看出,对于不同 SNR的噪声图片,由独立性准则所得到的最优滤波图像 SNR的值均接近于均方差方法得到的 SNR值,比相关系数方法得到的 SNR值要大.这说明独立性准则得到的最优滤波图像的视觉效果要优于相关系数方法.

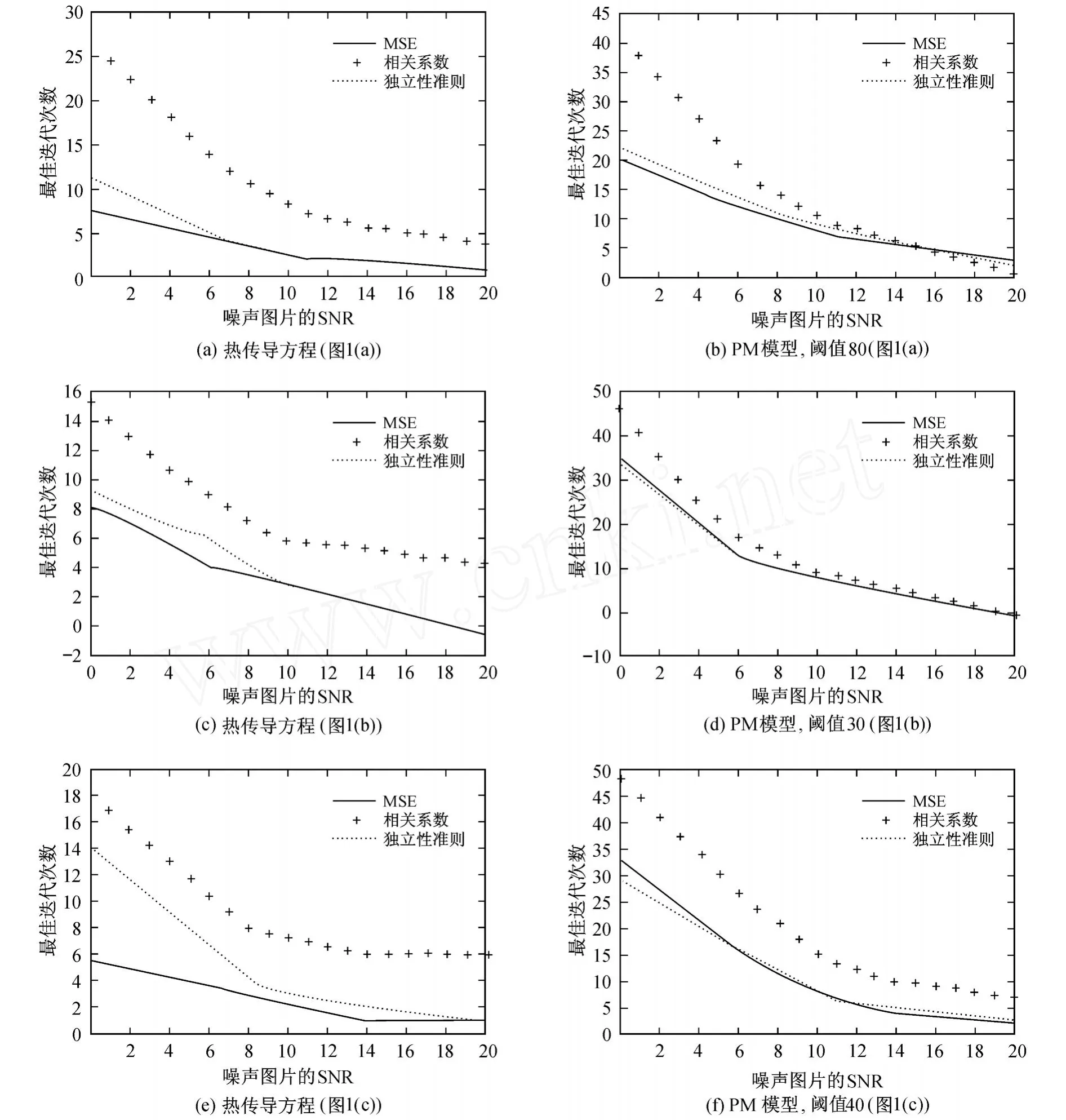
图 3 3种方法记录的最佳迭代次数的曲线图Fig.3 Graph of optimal stopp ing time noted by threemethods respectively

2.3 不同噪声图片 SNR情况下最优迭代停止时滤波图像 PSNR的比较

图 5为不同 SNR的噪声图片用 3种方法在最优迭代停止时滤波图像 PSNR的曲线图.具体操作过程类似 2.2节,区别是在最优迭代停止时记录滤波图像的 PSNR的值.

同 2.2节最优滤波图像 SNR的比较一样,图 5所反映的 PSNR的情况再次说明本研究提出的独立性准则所得到的结果与均方差方法得到的结果保持一致,优于相关系数方法.

3 结 束 语

本研究在分析已有最优停止准则的基础上,提出一种基于核密度估计的最优停止准则——独立性准则.该准则从随机变量之间的独立性出发考虑问题.数值实验的结果表明,独立性准则所确定的最优停止次数接近于均方差方法的结果,优于相关系数方法,且不需要任何关于噪声的附加信息.在最优停止时刻,滤波后图像的 SNR和PSNR的值说明,独立性准则得到的滤波图像的视觉效果要优于相关系数方法.不足之处在于,独立性准则在计算中涉及到二维随机变量的联合概率密度和边际概率密度的无参数核密度估计,计算量较相关系数方法大.下一步还将继续对核密度估计法的相关问题进行深入探究.

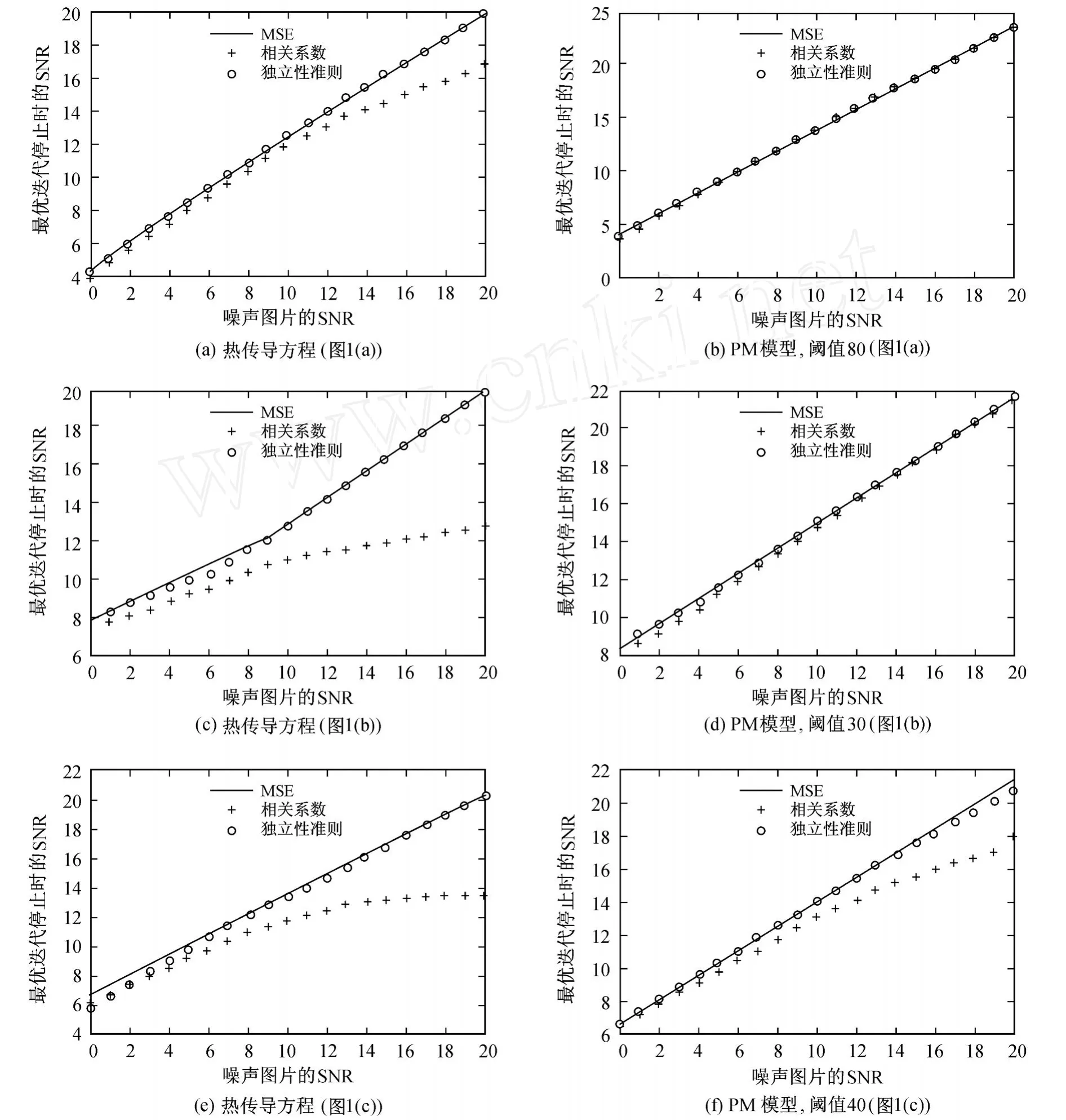
图 4 3种方法记录的最优迭代停止时滤波图像的 SNR值的曲线图Fig.4 Graph of SNR of f iltered images at optimal iterative tim e

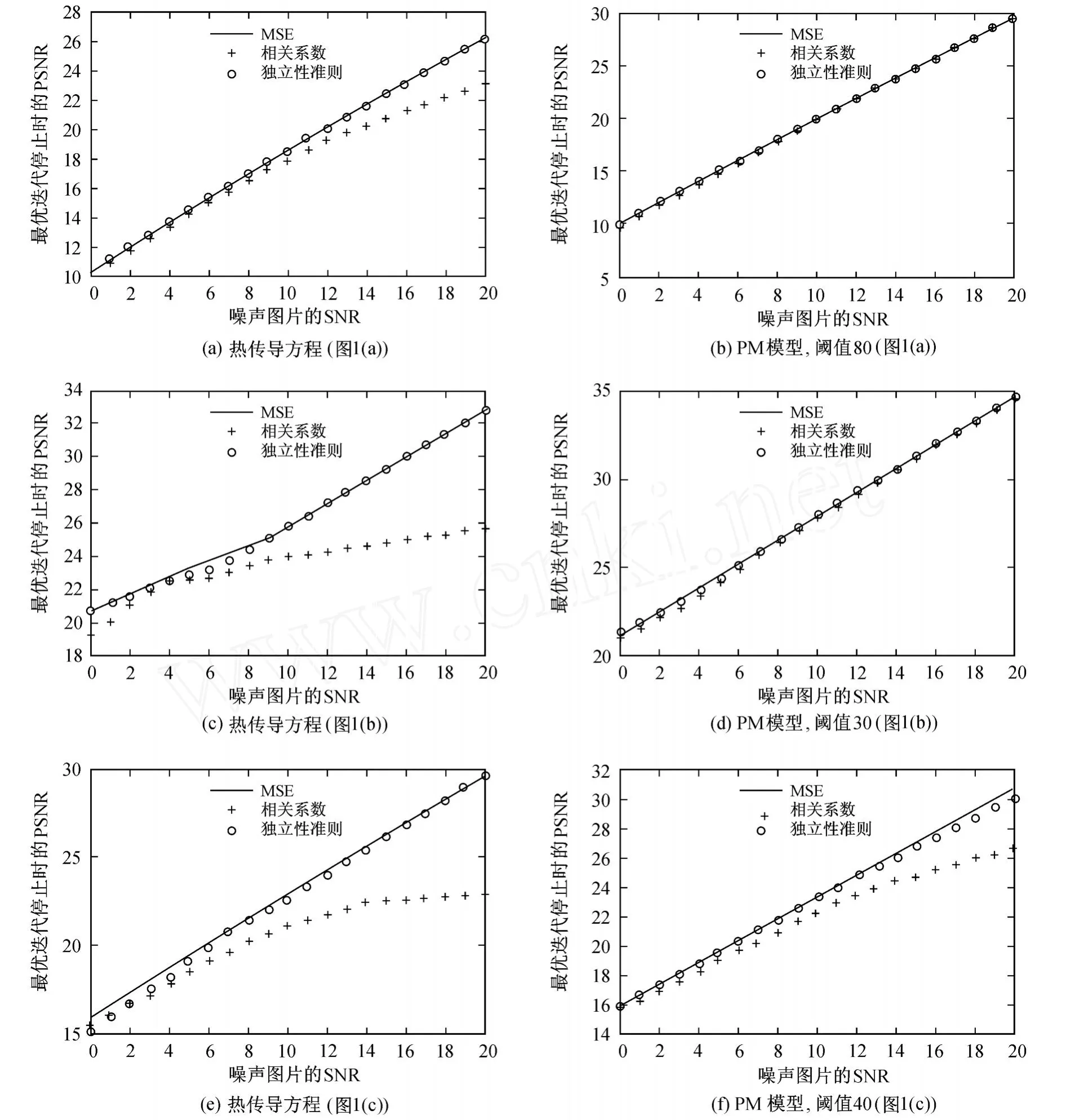
图 5 3种方法记录的最优迭代停止时滤波图像 PSNR值的曲线图Fig.5 Graph of PSNR of f iltered imagesat optimal iterative time

致谢:感谢何幼桦老师的宝贵建议.

[1] KOENDERINK J J. The structure of images[J].Biological Cybernetics,1984,50:363-370.

[2] PERONA P,MAL IK J.Scale-space and edge detection using anisotropic diffusion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(7):629-639.

[3] WEICKERT J.Anisotropic diffusion in image processing[C]∥ECM I Series.Germany:Teubner-Verlag,1998:1-152.

[4] CHEN PY,WANG YD.Fourth-order partial differential equations for image inpainting[C]∥IEEE on Audio,Language and Image Processing.2008:1713-1717.

[5] MRAZEK P,NAVARA M.Selection of optimal stopping time for nonlinear diffusion filtering[J]. International Journal of Computer Vision,2003,52(2/3):189-203.

[6] BARCELOS CA Z,BOAVENTURA M,SILVA E.A well balanced flow equation for noise removal and edge detection[J].IEEE Transactions on Image Processing,2003,12(7):751-762.

[7] WEICKERT J.Coherence-enhancing diffusion of color images[J].Image and Vision Computing,1999,17:201-212.

[8] BRADLEY R C. Basic properties of strong mixing condition:a survey and some open questions[J].Probability Surveys,2005,2:107-144.

[9] 施利亚耶夫.概率[M].3版.北京:高等教育出版社,2007:129-189.

[10] 张波,张景肖.应用随机过程 [M].北京:清华大学出版社,2000:1-5.

[11] WASSERMAN L.All of nonparametric statistics[M].New York:Springer,2006:134-153.

[12] ROUSSON M,CREMERS D. Efficient kernel density estimation of shape and intensity priors for level set segmentation[J].Med Image Comput Assist Interv,2005,8(2):757-764.

Optimal Stopp ing for Image Smoothing Based on Kernel Density Estimation

L IYi, WANG Yuan-di
(College of Sciences,ShanghaiUniversity,Shanghai200444,China)

Optimal stopping has been an important issue in image smoothing based on partial differential equations.According to the independence of random variablesand the kernel density estimation,a novel op timal stopp ing criterion isp roposed,which can be used w ithout know ing the noise variance.Numerical experiments show consistency between the resultsobtained with the proposed method and thatof themean square error(MSE)method.The criterion is app licable at various noise levels.

partial differential equation; image smoothing;correlation coefficient;kernel density estimation;op timal stopp ing

TP 391

A

1007-2861(2011)01-0103-08

10.3969/j.issn.1007-2861.2011.01.018

2009-09-15

国家自然科学基金资助项目(10572080,10671118)

王远弟 (1965～),男,副教授,博士,研究方向为偏微分方程、数字图像处理等.E-mail:ydwang@mail.shu.edu.cn

(编辑:赵 宇 )

在图像处理过程中,图像数据的迭代运算不可缺少,特别是去除图像噪声的预处理过程.迭代运算的关键问题就是如何确定迭代的次数,或者说迭代运算何时停止,从而使得图像处理得到最佳的效果.因此,解决该问题将给图像处理带来指标性的作用,使得在进行相应的图像处理时不必借助人工干预,在算法达到最佳效果后能够自动停止迭代运算.本研究旨在以图像噪声去除为例探索该问题的解决办法.

图像的去噪声处理即图像的平滑,主要是为了去除实际成像过程或传输过程中由于噪声的干扰而导致的图像失真.噪声一般由其概率特征来描述,如常见的高斯噪声、椒盐噪声等.近年来兴起的偏微分方程图像平滑方法在数字图像处理领域得到了充分的应用.

1984年,Koenderink[1]提出,含有噪声的图像U0(x,y)与高斯滤波器的卷积等价于求解一个各向同性的热传导方程.不过热传导方程的同性扩散效应在平滑去除噪声的同时也模糊了边缘,使得图像丢失了一些有用的信息.为了兼顾平滑和边缘保持,Perona等[2]提出一个以边缘为扩散系数的各向异性扩散模型 (Perona-Malik模型,简称 PM模型).PM模型能够实现边缘的保持,但数值实验结果显示,在达到一定迭代次数之后,图像会呈现出分块现象,从而影响到图像处理的效果.随后,许多学者提出了各种各样的偏微分方程图像平滑以及去除噪声的模型[3].这些模型都力求最大限度地平滑去除噪声,最小限度地防止边缘和图像信息遭到破坏.这就需要有一种迭代停止准则对图像平滑起到控制作用,防止过度平滑所造成的图像细节信息的丢失.事实上,图像处理过程中的最佳停止问题几乎存在于每个图像处理过程中,比如图像修复问题[4]等.