基于组合分类挖掘模型的调查问卷数据预处理
2011-10-18李春林李冬连万平
李春林,李冬连,万平
(河北经贸大学数学与统计学学院,石家庄050061)
基于组合分类挖掘模型的调查问卷数据预处理
李春林,李冬连,万平
(河北经贸大学数学与统计学学院,石家庄050061)
文章在Bates和Granger对时间序列的组合预测模型的理论基础上,灵活运用数据挖掘的思维和Clementine数据挖掘软件中的相关节点,充分利用问卷中已有信息构造组合分类数据挖掘模型,对《影响中国人际关系和谐因素调查问卷》进行分类了预处理。
调查问卷;数据挖掘;数据预处理;组合分类模型
0 引言
问卷调查所获的微观数据,尤其在调查范围广、人群杂、问卷数量多的情况下,难免会出现工作失误、被访者不配合、抽样方法选取不当、问卷设计不合理等现象,致使问卷数据中存在各种不一致、缺失、错误、冗余以及含有与定量分析方法不符的数据等情况。要保证问卷调查分析的质量,对原始数据进行清理、集成、变换和规约等预处理过程不容小觑。
面对问卷数据中的各种不符合要求,尤其是存在缺失值的情况,目前常用的方法有删除问卷、删除缺失值、插补法等。最直接和简便的方法莫过于删除问卷和缺失值,但这很可能致使结果偏差严重。并且这两种方法的前提条件是问卷量很大,不符合要求的问卷很少(低于10%)[1]。插补法是利用其他数据代替和估算缺失值。如利用回归、众数、判定树归纳、贝叶斯推断方法等建立一个预测模型,利用模型的预测值代替缺失值。尽管这些方法相对复杂,但能够最大程度地利用现存数据所包含的信息。
本文所研究问卷数据来自于“当代中国影响人际关系和谐因素问卷调查”,该项调查共获得有效问卷2972份,其中有以下几种形式数据需要做相应预处理:
(1)人口统计学数据的预处理。这部分主要是对数值数据进行离散化处理和对分类数据进行概念分层处理。如:本文将年龄离散化为30岁以下(不包括30岁)、30至50岁(不包括50岁)及50岁以上三个阶段;将学历分为中小学、大中专、本科、研究生四个层次。
(2)缺失值预数理。2972份问卷中的被访者基本信息部分至少存在一项缺失的问卷量达187份;在关于当前社会道德水平(Q15)和我国民主建设(Q28)满意度的调查题目中,问卷在答案最后设置了“说不清”选项,且分别有106个(3.57%)和497个(16.72%)被访者选择了该选项。但“说不清”选项并不是按Likert量测标准设置,不适合定量建模型分析,因此将其视为问卷设计不合理而作缺失值处理。
因为缺失值问卷数量比重较大,不宜作删除处理。本文试图利用分类模型根据已有问卷信息进行有指导地学习,建立一个分类模型,再利用所得模型对缺失值进行分类预测。因为不同的模型有自身不同的优点和缺点:神经网络等非线性方法的精度往往要高于(线性)判别分析、Logistic回归、线性规划等线性评分方法;而Logistic回归、判别分析、线性规划等方法的稳健性则比神经网络方法要好[2]。因此,本文试图用组合模型对缺失值进行分类预处理。同时考虑到问卷数据不仅有数值型数据,也有分类型数据,而判别分析只适用于数值型数据,因此组合模型由Logistic回归、CHAID决策树和神经网络模型构成。本文将以对Q28中“说不清”的预处理过程为例进行说明。
1 组合分类模型的原理
1.1 组合分类模型
对于组合模型的运用,学术界最常用的是Bates和Granger(1969)[3]对时间序列的组合预测模型,如文献[3]~[6]。而对于组合分类模型的研究尚未见到文献记载,本文在借鉴Bates和Granger关于时间序列的组合预测模型的基础上,对组合预测模型进行适当修正,构造出组合分类模型。假设已知一个问题有K个类别,记为c1,c2…,ck;有m个分类模型适用于该问题,分别记为f1,f2,…,fm;pij=p(ci(fj)),表示第j种分类模型判断某个样本单元问卷单元属于第i个类别的概率;wj为第j个模型在组合分类模型中的权重。
因此,组合分类模型可表示为:

1.2 权重的确定
组合模型中,权重的选择非常重要。常用的权重选择方法有算术平均法、标准差法、方差倒数法、均方倒数法、主成分分析法、德尔菲法、最优加权法等。本文使用最优加权法,即对误差平方和在最小二乘法准则下求解如式(2)所示的线性规划问题:

如果定义Im=(1,1,…,1)T,且存在协方差矩阵∑,则有:

用Lagrange乘数法求解(3)得:

即:
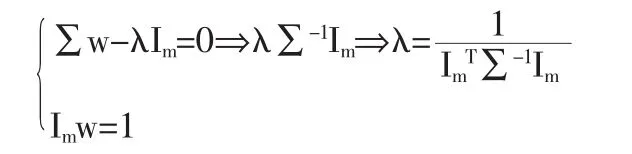
2 单一分类模型及结果
2972份问卷中,有62份因为信息缺失严重而无法进行预处理,故将这些问卷删除。剩下2910份问卷中,有494个被访者在Q28题中选择了“说不清”选项,因此将其视为缺失值进行预处理。并以选择其他选项的2416个有效问卷建立组合分类模型,对选择“说不清”的494个问卷进行分类预测。
建立模型之前,将2416个有效问卷通过设置随机种子的方式进行随机抽样,随机选取70%作为训练问卷用来建立分类预测模型,30%当作测试问卷用来检验模型的稳健性。本文单一分类模型的拟合过程分别通过Clementine数据挖掘软件中的Logistic节点、CHAID决策树节点和RBF神经网络节点实现。
2.1 Logistic回归分类模型
本文因为反应变量为4Likert测量形式,即受访者对我国民主建设的态度是满意、比较满意、不满意还是很不满意,因此采用多项logit模型进行分析。将产生三个logit(即对数发生比),并将“很不满意”定义为参照类,如式(5):

其中p1,p2,p3,p4分别表示被访者对我国当前民主建设态度是满意、比较满意、不满意和很不满意的概率,且p1+p2+ p3+p4=1。多项logit模型将产生三套回归系数系数:满意对比很不满意的对数发生比,比较满意对比很不满意的对数发生比,不满意对比很不满意的对数发生比。
2.2 CHAID决策树分类模型
CHAID决策树模型主要适用于市场调查和社会调查过程分析。CHAID的全称是Chi-squared Automatic Interaction Detector(卡方自动交互检测)。1980年,由Kass等人提出,它的理论构想主要来源于决策树模型,根据反应变量在解释变量上的分布来进行分类,适用于分类和序次等级数据的分析,是一种以目标最优为依据,具有目标选择、变量筛选和聚类功能的分析方法[8]。它的基本分析思路是X2自动交叉检验[9],首先选定分类的反应变量,然后用解释变量与反应变量进行交叉分类,产生一系列二维分类表。分别计算二维分类表X2的值或似然估计统计量,以最大统计量的二维表作为最佳初始分类表,并继续使用分类指标对目标变量进行分类,重复上述过程直到满足分类条件为止。
2.3 径向基神经网络分类模型
径向基(RBF)神经网络是由输入层,隐含层和输入层构成的3层前向网络。在RBF网络中,隐含层节点通过径向基函数执行一种非线性变化,将输入空间映射到一个新的空间,输出层节点则在该新的空间实现线性加权组合[10]。径向基函数是径向对称的标量函数,定义为空间一点x到某一中心xc的欧式距离的单调函数k(‖x-xc‖),x∈RN,最常用径向基函数为高斯核函数:

其中σ为带宽,控制函数的径向作用范围,xc是核函数中心。
通过Clementine数据挖掘软件中相关节点的拟合,得到了单一模型对训练集和测试集的拟合检验结果,如表1所示。
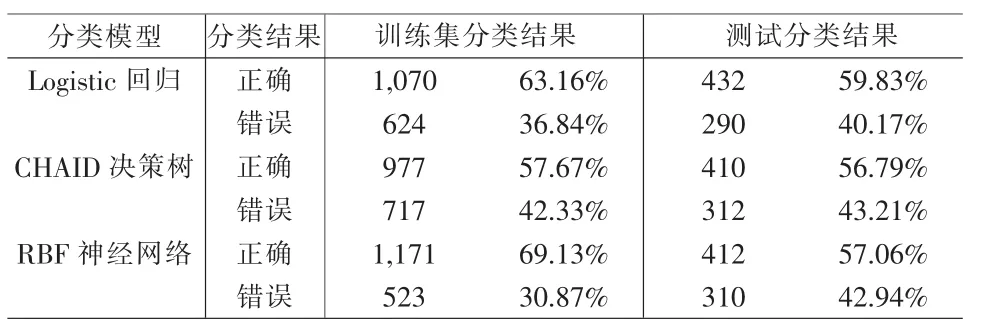
表1 单一模型对训练集和测试集的分类结果
4 组合分类模型建立过程及结果
从表1可以看出3个单一模型各有优缺点:RBF神经网络模型对训练集的拟合精度达69.13%,但对测试集的分类精度却只有57.06%;而Logistic回归模型和CHAID决策树模型尽管对训练集的拟合精度分别只有63.16%和57.67%,但对测试集的分类精度仍分别达59.83%和56.79%。因此,从这些数据也进一步证明了参考文献[3]给出的结论。
根据组合模型的理论,设测试集中第r个样本单元在Q28上实际类别为yi,其中ci=1,2,3,4;r=1,2,…722。分类误差为eir=yi-cir,即第j种分类模型在第r个样本单元上的分类误差。组合误差为er(第r个样本单元上的分类预测):

令W=[W1,W2,W3]T;Σ=[e1r,e2r,e3r]T,为第j个分类模型的分类误差向量,则组合分类模型的误差矩阵为e=[Σ1,Σ2,Σ3],其协方差矩阵为:

进一步得到其逆矩阵为:


因此,组合分类模型中,Logistic回归模型的权重为0.3333,CHAID决策树模型的权重为0.3704,RBF神经网络模型的权重为0.2963。
因此,本文组合分类模型可表示为如式(8):


由Clementine分析结果可知,组合模型对测试集的分类准确度为62.88%。因此,最优组合分类模型从总体上起到了提高分类准确度的作用,用该模型对Q28中494个选择了“说不清”选项的问卷进行分类预处理更为有效和可信,其结果如表2所示。
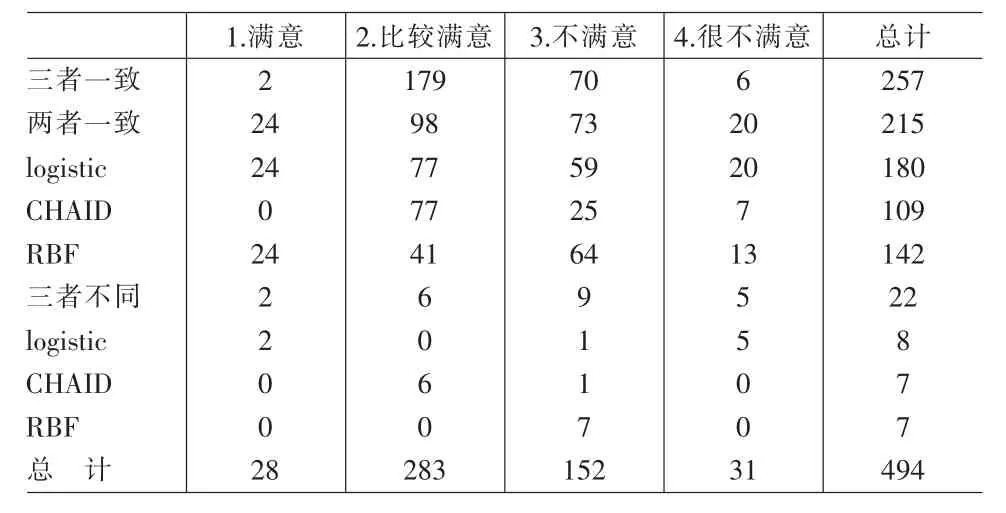
表2 组合分类模型预处理结果
4 结论
本文从问卷的特点出发,借助Clementine数据挖掘软件构建了适合于分类数据分析的组合分类模型。并有效地对“影响当代中国人际关系和谐因素的问卷调查”所获问卷数据的缺失值进行预处理。尽管数据预处理过程非常烦琐和耗时,但能有效地提高数据预处理结果的准确度和可信度,并且能大大提高数据挖掘模式的质量。
[1]朱胜,冯能亮.市场调查方法与应用[M].北京:中国统计出版社, 2004.
[2]石庆炎.一个基于神经网络——Logistic回归的混合两阶段个人信用评分模型研究[J].统计研究,2005.
[3]Bates T M,Granger C M J.The Combination of Forecasts[J].J.Operational Research Society,1969,(20).
[4]权轶,张勇传.组合预测方法中的权重算法及应用[J].科技创业月刊,2006.
[5]赵韩,许辉等.最优组合预测方法在家用汽车需求预测中的应用[J].工业工程,2008.
[6]刘志杰,季令等.基于径向基神经网络的集装箱吞吐量组合预测[J].同济大学学报(自然科学版),2007.
[7]王济川,郭志刚.logistic回归模型方法与应用[M].北京:高等教育出版社,2001.
[8]何凡,沈毅,叶众.CHAID方法在居民卫生服务需求研究中的应用[J].数理统计与管理,2006.
[9]Chaturvedi A,Green P E,et al.SPSS for Windows,CHAID6.0 [J].Journal of Marketing Research,1995,(21).
[10]马超群,兰秋军,陈为民.金融数据挖掘[M].北京:科学出版社, 2008.
(责任编辑/亦民)
O212
A
1002-6487(2011)05-0011-03
国家社会科学基金重点资助项目(2007AZX004)
李春林(1963-),男,河北任县人,教授,研究方向:市场调研和数据挖掘。
万平(1984-),男,湖南湘乡人,硕士研究生,研究方向:市场调研和数据挖掘。
