基于TOPSIS法的数控车床刀架系统故障分析*

张英芝 何 宇 申桂香 李怀洋 刘 葳

(①吉林大学机械科学与工程学院，吉林长春130025;②长春理工大学生命科学技术学院，吉林长春130022)

数控机床是机、电、液、控一体化的复杂系统，其可靠性一直是困扰机床主机生产厂和用户的关键问题［1-2］，研究表明刀架系统是影响数控机床可靠性的关键子系统［3］，很多学者从可靠性设计、可靠性建模及故障分析等角度对刀架系统进行了研究报道［4-6］。毋庸置疑，提高刀架系统的可靠性水平是提高整机可靠性的必经之路，但刀架系统故障机理复杂，故障模式多样，对每一种故障模式同等对待显然是不切实际的，迫切需要找出影响刀架系统可靠性的关键故障模式。故障模式、影响及危害性分析(FMECA:Failure Mode，Effects，and Criticality Analysis)仅从故障模式概率、故障影响及基本故障率3个因素对系统或部件的危害性进行评价，忽略了维修性等其他方面的影响。本文综合考虑故障发生频率、维修时间、维修费用和对相关部件的影响程度，采用解决多目标决策问题的逼近理想方案的序数偏好方法(TOPSIS:Technique for Order Preference by Similarity to an Ideal Solution)对刀架系统故障模式重要性进行排序，确定影响刀架系统可靠性的关键故障模式。

1 刀架系统故障模式、影响及危害性分析

某系列数控车床刀架系统在考核期共发生24次故障，将这些故障分为6个故障模式，故障表现形式及其他信息如表1所示。根据文献［7］中FMECA算法，得到各故障模式危害度值，如表2所示。数控车床的累积工作时间为115 805 h(双班制)。

表1 刀架系统故障情况描述

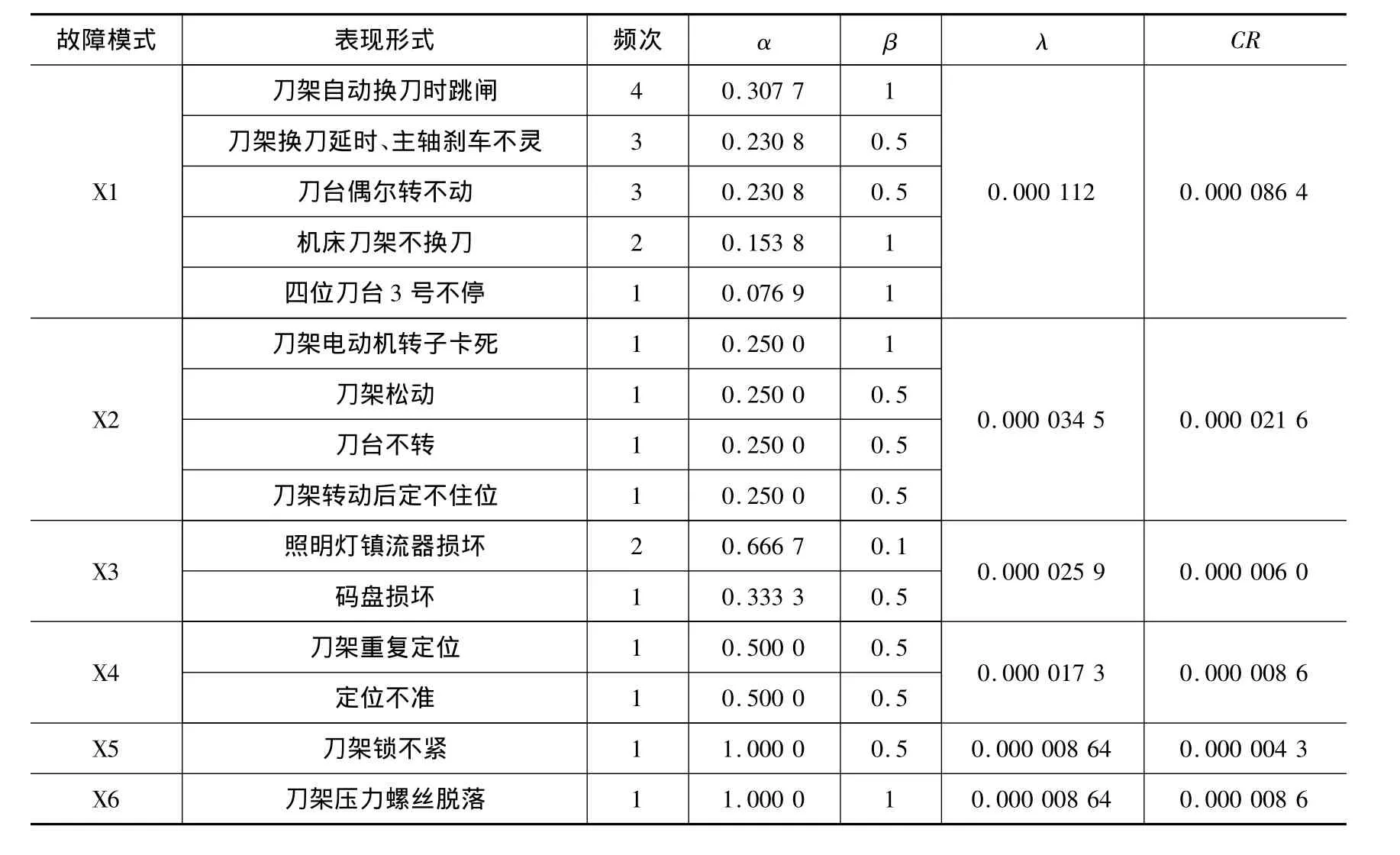
表2 刀架系统FMECA表

FMECA仅考虑了3个因素的贡献，忽略了维修时间、维修费用等其他重要方面。下面应用TOPSIS法从故障发生频率、维修时间、维修费用和对相关部件的影响程度4个方面对数控车床刀架系统进行故障分析。

2 TOPSIS法原理及数学模型

TOPSIS法是C L Hwang和K Yoon于1981年首次提出［8］，根据有限个评价对象与理想化目标的接近程度进行排序的方法，在现有的对象中进行相对优劣的评价。TOPSIS法是一种理想目标相似性的顺序选优技术，在多目标决策分析中是一种非常有效的方法。

TOPSIS法首先确定一个理想解和一个负理想解，然后找出与理想解距离最近且与负理想解距离最远的方案，作为最优方案。TOPSIS法中的距离是指(加权)欧式距离。理想解是设想的最好解，记为X+，它的各个属性值都达到各候选方案中最好的值;负理想解是设想的最差解X-，它的各属性值都达到各候选方案中最差的值。现有的n个方案中一般并没有这种理想解和负理想解，但通过设定理想解和负理想解，将每个实际的解与理想解和负理想解进行比较，如果其中有一个解最靠近理想解，同时又最远离负理想解，则该解是n个方案中最好的解，用这种方法可对所有的方案进行排序。

(1)决策矩阵归一化

对于n个评价目标m个评价指标的决策矩阵A，由于其物理维度不同，因此需按归一化理论把各指标规范化，即把各指标都统一变换到(0，1)范围内，成为规范化矩阵B，其矩阵元素Bij由式(1)得出。

(2)建立加权规范化矩阵

通过专家赋权得到各评价指标的权重向量W，建立加权的规范化矩阵X。

(3)求解

计算理想解X+和负理想解X-。

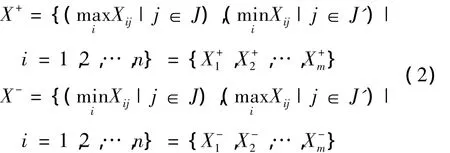
式中:J为效益型属性;J'为成本型属性集。

(4)计算距离尺度

即计算每个目标到理想解和负理想解的距离，距离尺度可以通过n维欧几里德距离来计算。

受水区内各分区地下水水位上限应是以降水入渗补给量最大、潜水蒸发损失最小、又不造成渍涝为准则，对城市地区，还应考虑地下建筑物的情况；下限应以地下水库调蓄最大、又能合理地控制地面沉降等生态环境问题为准则。对于地下水严重超采区，尤其是地下水水位大降深区，主要应研究如何合理控制地下水埋深，逐步减少地下水超采量。

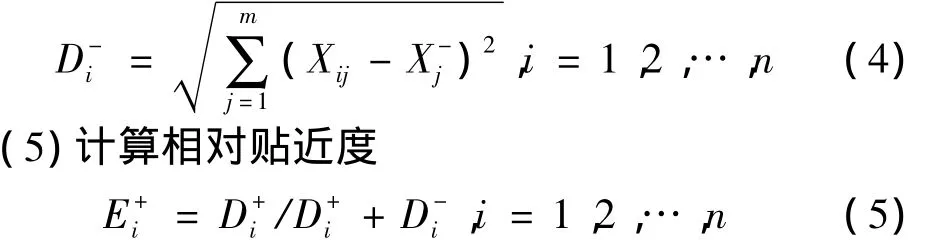
(6)根据贴近度排序

3 基于TOPSIS法的刀架系统故障分析

根据表1中各故障模式及表现形式的描述，由专家根据领域经验及刀架故障机理给出各故障模式在每个指标下的分数。由于维修费用涉及到备品备件成本、人工成本等不确定性因素，定量表示较困难，故从4个等级来衡量(具体见表3)，这样便得到每个指标的评分标准，如表3所示。

表3 维修时间、维修费用及对相关部件的影响程度评分标准

结合表1、表3得到刀架系统故障模式的决策矩阵，如表4所示。

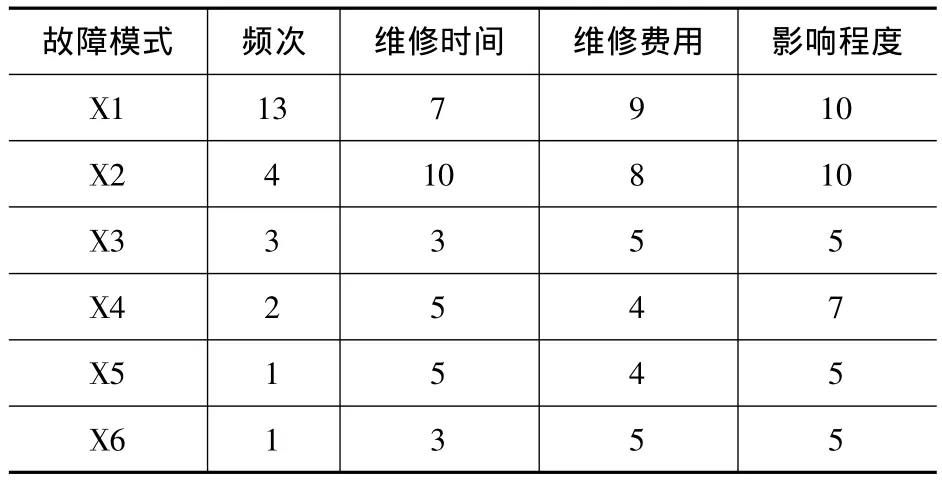
表4 刀架系统故障模式决策矩阵表

(1)决策矩阵 由表1可得决策矩阵A为

根据公式(1)对决策矩阵A归一化得到矩阵B

(2)结合刀架系统结构特点，请相关专家对故障频次、维修时间、维修费用及对相关部件的影响程度进行赋权。计算整理得加权向量:

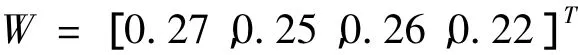
从而得到加权的规范化决策矩阵X

(3)计算理想解和负理想解 由式(2)得理想解为

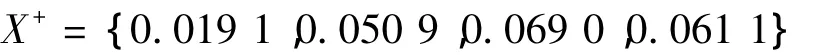
负理想解为

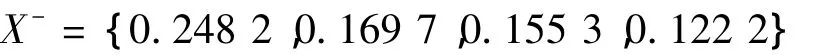
(4)计算距离尺度 由式(3)、(4)计算距离尺度，每个解到理想解的距离为

每个解到负理想解的距离为

(5)计算相对贴近度 根据式(5)计算每个解和理想解的相对贴近度(i=1，2，…，6)，计算结果为:

由表2和TOPSIS法计算的各故障模式的排序结果是有差异的，如图1所示(X1～X6依次代表表4中各故障模式)。刀架失调是影响该系列数控车床刀架系统的关键故障模式，分析其故障机理，发现刀架不换刀、换刀延时、刀台偶尔转不动等故障现象，无论从解决故障时间、维修方式还是维修费用、对其他系统的影响来看都是非常显著的。其次是运动部件失灵。TOPSIS方法计算结果表明移位、转位不到位的重要性高于零部件损坏，而FMECA无法判别这2种故障模式哪个更重要。分析其故障机理发现解决刀架重复定位和刀架定位不准这一类故障耗时较长，因为导致刀架定位不准的原因可能有:刀盘连接部件松动，霍尔元件开关位置不良，造成电气控制失效，刀盘到位的夹紧力不均等，经过故障检测和排除发现是由于定位牙盘内有污物引起，而这一故障机理将直接导致工件加工精度不稳定。分析零部件损坏这一故障模式发现，用较短的维修时间和较低的维修成本即可解决刀架压力螺丝脱落这一故障，且对刀架系统及整机可靠性的影响较小。可见，由TOPSIS法计算的故障模式重要性排序更加合理，符合工程实际。

4 结语

将TOPSIS理论引入数控车床刀架系统故障分析中，分别计算理想解和负理想解，距离尺度和相对贴近度，最终得出各故障模式的重要性排序。通过和危害度排序结果的比较分析发现，在考虑故障的维修时间、维修费用以及对相关部件的影响程度时，排序结构更准确、合理，应用TOPSIS法的故障分析程序简便、易于操作，分析结果符合工程实际，本文的研究工作对数控机床的可靠性设计及改进具有指导意义。

［1］贾亚洲，杨兆军.数控机床可靠性国内外现状与技术发展策略［J］.中国制造业信息化，2008(4):35-37.

［2］贾亚洲.提高数控机床可靠性—加快振兴装备制造业的关键［J］.中国制造业信息化，2006(6):42-43.

［3］张英芝，申桂香，吴甦，等.基于模糊理论的数控车床故障分析［J］.中国机械工程，2009，19:2354-2357.

［4］陈水生.数控车床转塔型电动刀架控制系统设计［J］.制造技术与机床，2008(5):20-22.

［5］张英芝，申桂香，薛玉霞，等.随机截尾数控车床刀架系统故障过程［J］.吉林大学学报(工学版)，2008(S2):113-116.

［6］于捷，石耀霖，申桂香，等.基于二元决策图的数控机床转塔刀架系统重要度分析［J］.制造技术与机床，2009(3):132-136.

［7］张海波，贾亚洲，周广文，等.数控系统故障模式、影响及危害度分析(FMECA)［J］.中国机械工程，2004(6):491-494.

［8］岳超源.决策理论与方法［M］.北京:科学出版社，2003.