板材多点成形使用弹性垫后回弹的数值模拟

2011-10-18杨建鸣任振中

制造技术与机床 2011年9期

杨建鸣郝洁任振中

(内蒙古科技大学机械工程学院，内蒙古包头014010)

多点成形技术的基本思想是将实体模具离散化，由一系列规则排列的基本体组成的“柔性多点模具”取代传统冲压成形的实体模具。该技术在板料三维曲面成形方面有着广阔的应用前景，特别适合于曲面板制品的多品种小批量生产及新产品的试制。目前，已经在高速列车流线型车头覆盖件、潜艇外板以及人脑颅骨修复体等成形件的数字化制造中得到广泛应用。

板材成形时，回弹是不可避免的现象。在外载荷作用下板材的变形由塑性变形和弹性变形两部分组成，当外载荷卸掉后，塑性变形保留下来了，而弹性变形则回复，使成形件的形状和尺寸都发生与加载时变形方向相反的变形，这很大地影响了成形件的尺寸精度。因此，采用数值模拟技术研究多点成形中的回弹可有效地预测和减小回弹，从而提高成形尺寸精度［1］。

1 板材回弹模拟的有限元基本算法

1．1 基本理论

板材的回弹模拟即要求有显式分析以模拟动态成形过程，还需要有隐式分析以模拟卸载后的静态回弹阶段。对于非线性结构静动力分析，LS-DYNA可以交替使用隐式求解和显示求解，进行薄板冲压成形的回弹计算［2］。首先用ANSYS/LS-DYNA程序模拟动态成形过程，然后将变形后的几何形状和应力输入到ANSYS隐式分析中求解，具体的分析过程如图1所示。

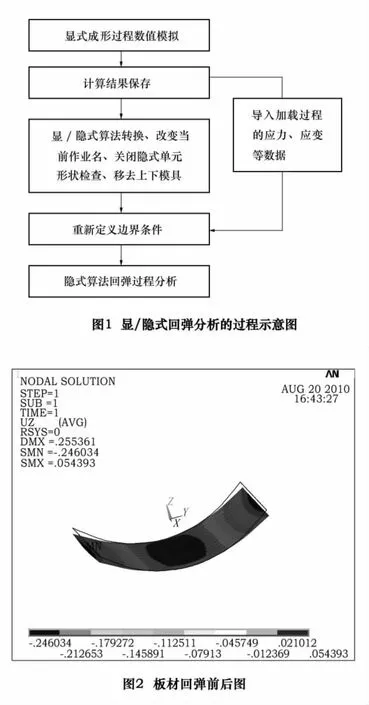
1.2 有限元模型

对钢板的回弹进行数值模拟，材料为各向同性，弹性模量E=207 GPa，泊松比 μ=0.3，屈服强度 σs=128.5 MPa，切向模量Etan=345 MPa，密度 ρ=7 845 kg/m3。板材大小L=96 mm×64 mm。基本体采用12×8排列，间距是8 mm，基本体半径5 mm。板材和基本体单元模型均采用SHELL163壳单元，其中板材分为6 144个单元，上基本体分为6 828个单元，下基本体分为6 828个单元。

图2所示是板厚为1 mm，目标曲率半径为R=50 mm的圆柱面回弹前后图，其中虚线部分为回弹前的形状。

2 弹性垫厚度对回弹的影响

在多点成形中，板材的变形外力来自冲头对板材的接触作用，基本体冲头的集中力直接作用于板材，成形件上不可避免地会产生压痕［3］。为了有效地分散接触压力从而抑制压痕的产生，不得不在冲头和板材之间使用弹性垫。图3为未使用弹性垫和使用3 mm弹性垫的板材成形图，可以看出弹性垫能很好地抑制压痕的产生。

当然，不同的弹性垫厚度对压痕的抑制效果也是不同的，图4为使用1 mm、2 mm、3 mm弹性垫后，板材的塑性应力图，其中 A、B、C分别对应1 mm、2 mm、3 mm厚度的弹性垫。从图中可以看出，弹性垫越厚，对压痕的抑制效果越好，使用3 mm的弹性垫已经可以很好地抑制压痕了。

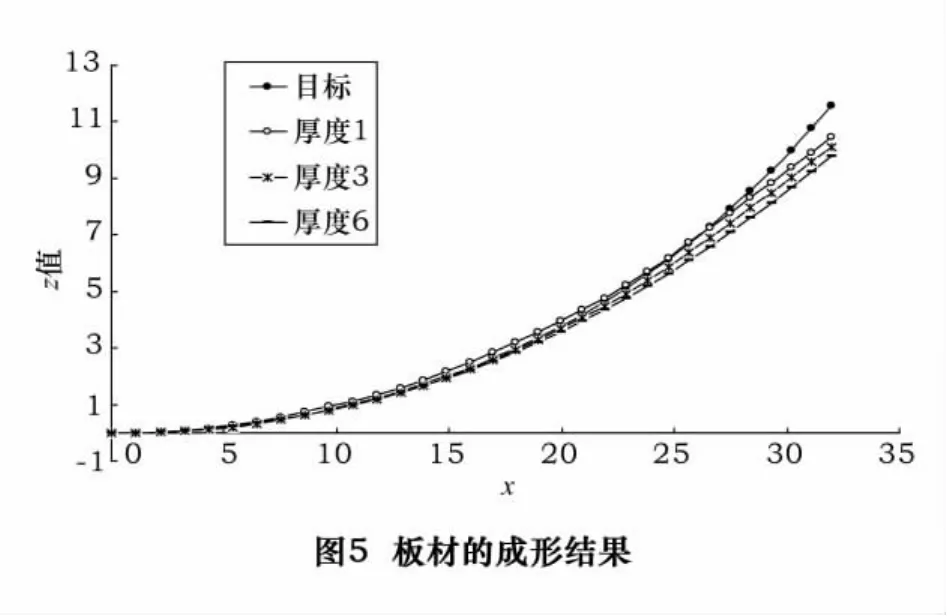
但弹性垫的厚度又直接影响到板材回弹后的成形精度，图5为目标曲率为50 mm的圆柱面分别使用1 mm、3 mm、6 mm弹性垫时，成形回弹后的形状。从图中可以看出，随着弹性垫厚度的增加，回弹后板材形状会逐渐偏离目标形状。

3 对成形结果的补偿

从以上的分析可以看出，随着弹性垫厚度的增大，虽然可以很好地抑制压痕的产生，但是成形精度也会受到影响。为了有效地提高成形精度，提出了对成形结果的补偿。

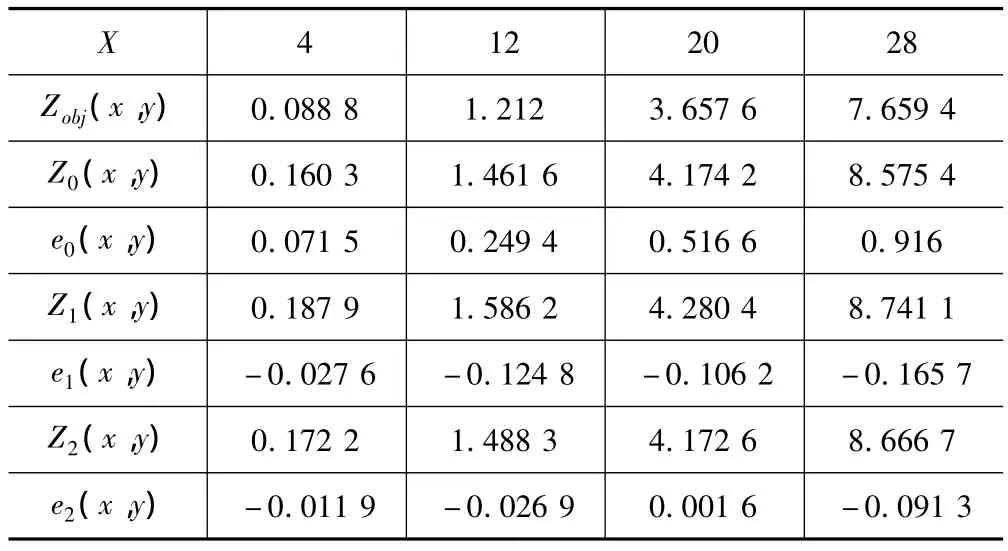
表1 圆柱面的 Zk(x，y)、ek(x，y)

表2 基本体的Sk(x，y)

使用3mm的弹性垫抑制压痕的效果明显好于2mm的弹性垫，但他们的成形精度却差不多，因此对结果进行补偿时，采用3mm的弹性垫。

设 Zobj(x，y)为目标成形曲面，Zk(x，y)为第 k 次修正成形件曲面，则与目标曲面的误差为

式中，Sk(x，y)为由基本体群构造的第k次模具修正曲面［4］。

表1为板材未补偿和第一、第二次修正的Zk(x，y)值，第一行为板材的X坐标，Z0(x，y)为未补偿时的值。模具未进行修正时可以看出距离圆柱面中心越远，误差越大，这也正是离中心越远回弹值越大所导致的。经过两次修正，成形件曲面与目标曲面的误差有了明显的减小，板材的精度也得到了很大的提高。表2为Sk(x，y)值，是回弹补偿时对基本体高度的调节。