压缩三维走时表提高克希霍夫偏移计算效率
2011-10-17杨长春李波涛
王 珺,杨长春,李波涛
(1.石油大学 信息与控制工程学院,东营257061;2.中科院地质与地球物理研究所,北京100029;3.中国科学院 兰州地质研究所,兰州730000)
压缩三维走时表提高克希霍夫偏移计算效率
王 珺1,杨长春2,李波涛3
(1.石油大学 信息与控制工程学院,东营257061;2.中科院地质与地球物理研究所,北京100029;3.中国科学院 兰州地质研究所,兰州730000)
地震波走时是克希霍夫叠前深度偏移的重要参数。三维克希霍夫偏移成像由于需频繁读取大数据量的走时表文件,所以计算效率不高。这里提出一种通过压缩三维射线追踪走时表,来提高克希霍夫偏移计算效率的方法:首先规划一个具有规则网格控制点并覆盖所有走时表点集的最小长方体区域,然后以三维三次B样条函数为插值基函数进行最小二乘法曲面体拟合,求出规则网格控制点的数值并以数组形式存储入内存,采用稀疏化存储进一步节省了内存空间。在偏移成像时,再由这些规则网格控制点的数值,使用线性插值公式解编出走时表。实际资料算例验证了该走时表压缩方法不仅近似精度高,计算稳定度高,计算效率高,而且由于省去了频繁进行大数据量走时表文件的读写操作,所以克希霍夫偏移的计算效率提高了二倍以上。
克希霍夫偏移;计算效率;三维走时表压缩
0 前言
用射线追踪方法计算地震波走时是克希霍夫叠前深度偏移的基础。在三维地震克希霍夫偏移成像过程中,三维射线追踪的走时表往往具有相当大的数据量,通常作为专门的文件来存储,成像时需频繁地读取此走时表文件,这样势必造成成像计算效率不高。如果能够将大数据量的三维射线追踪的走时表压缩存储,用有限个数值点来代替,直接以数组的形式存储在内存中,就省去了频繁地进行较大数据量文件的读写操作,自然会提高克希霍夫偏移成像的计算效率。对射线追踪走时表进行的科学合理的压缩存储方法,还可用于提高正演模拟以及层析成像等的计算效率,具有重大的理论和现实意义。目前,国内、外有一些关于常规地震资料的压缩方法的研究工作(国内有郭洪升,陈俊良[1]、张军华,仝兆岐[2]、王喜珍等[3]、余平[4];国外有Averbuch、Meyer[5]、Bernasconi[6]、Wu[7]、Giancarlo[8]、E.J.Candès[9]、Cheng and Zhang[10])。
上述关于地震数据压缩的研究工作可大体分为两类:
(1)一类是有损失数据压缩,实际上就是采用基于变换的方法,比如小波变换方法,正交变换方法等。
(2)第二类是无损失数据压缩,如将地震资料转换为文本形式,然后对文本进行压缩。其中,有损失压缩方法压缩比较高,能满足信号传输的速度要求。
但是,在压缩前后资料的误差较大,这对后期地震资料的精确处理不利。无损失压缩方法虽然在压缩前后数据具有较小的误差,但压缩比很低,最高才能达到2,无法满足信号存储及传输的空间和速度要求。此外,上述地震资料压缩方法的压缩目的,均为减少地震资料数据体以节省存储空间或者利于远距离传输。通过压缩走时表来提高地震偏移计算效率方面的研究,尚未见到报道。
在三维克希霍夫偏移过程中,计算得到的射线追踪走时表属于大规模散乱数据。散乱数据指的是在二维平面上或三维空间中,无规则的、随机分布的抽样数据点。散乱数据的曲面拟合,是指通过这一系列无规则的抽样数据点构造一个光滑的曲面,以实现在对这些散乱数据进行分析时,不但可以知道抽样位置的数值,还可以知道任意位置的数值。鉴于三次B样条函数具有连续二阶导数的光滑性、计算的快速性,控制节点的稳定性,在满足计算精度的前提下,对于插值和曲面拟合具有最优性。作者在本文提出了采用三次B样条函数曲面体最小二乘拟合,对三维射线追踪走时表进行压缩存储,以提高克希霍夫偏移成像计算效率的方法。由于本算法最小二乘法线性方程组的系数矩阵为稀疏矩阵,且是非零元素规则排列(为25个条带,带宽均为5的带状结构),所以采用稀疏矩阵存储方法对矩阵进行存储节省了内存空间。实际三维地震资料验证了本算法具有很好的适用性,可以保证压缩拟合的计算效率和计算精度,提高了三维克希霍夫叠前深度偏移的计算效率。
1 Kirchhoff偏移基本原理
根据Claerbout成像原理,介质中的成像点r处的偏移成像,可以由该点处的散射波场与入射波场的比值,在频率域积分得到。即
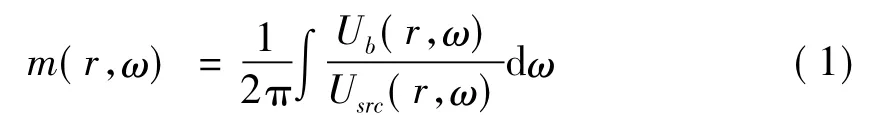
其中 成像点r处的散射波场为从检波点处反传播到介质中,使能量集中于成像点r处的反传播场Ub(r,ω),入射波场为来自震源的源场Usrc(r,ω)。
根据半空间压力场的Kirchhoff积分公式,反传播场见式(2)。

入射波场见式(3)。

其中r、rs、rd分别为成像点、源点和检波点的坐标(x,y,z);U(rd,ω)为频率为 ω 时检波点rd处的压力场;n⇀为检波点rd所在曲面的法向量;G*(rd,r,ω)为成像点r到检波点rd的格林函数的傅氏变换的复共轭,G*(rd,r,ω)=A(rd,r)exp(-iωT(rd,r));A(rd,r);T(rd,r)为沿着从成像点r到检波点rd的射线的振幅和走时;F(ω)为源函数的傅氏变换;G(rs,r,ω)为成像点r到震源rs的格林函数的傅氏变换,G(rs,r,ω)=A(rs,r)exp(iωT(rs,r)),A(rs,r)、T(rs,r)为沿着从源点rs到成像点r的射线振幅和走时。上述振幅和走时,均可以通过射线追踪得到。由上述讨论可见,成像点处的走时数据是计算格林函数的必要参数,因而也是克希霍夫偏移的重要参数。但三维射线追踪的走时表往往具有相当大的数据量,需要作为一个文件来存储,在成像时需频繁地读取这个大数据量的走时表文件,从而导致偏移成像的计算效率不高。
2 三维走时表压缩
在三维情况下,单炮射线追踪的走时表用t=f(x,y,z)表示,其中(x,y,z)是三维空间中离散数据点的坐标,t是对应于此点的走时值。对三维系统的散乱数据进行曲面拟合和数据压缩,实际上是利用已知的散乱数据,描述连续曲面的过程。在曲面拟合时,首先寻找一个光滑的插值基函数,然后确定散乱数据在三维立体中坐标(x,y,z)的范围,规划出一个具有规则网格控制点并包含所有散乱数据点集的最小长方体区域,再利用最小二乘法拟合,求出规则网格控制点的数值。在存储时,只需要保留这些有限个规则网格控制点的数值,就可以代表原有的散乱数据。根据偏移成像计算的需要,使用线性插值公式就可以解编出原有的散乱数据。
2.1 选取插值基函数
就现有的插值方法而言:
(1)高次函数插值的计算量大,有剧烈振荡,数值稳定性差。
(2)在分段插值中,分段线性插值在分段点上仅连续但不可导,分段三次埃尔米特插值仅能保证一阶导数连续,因此光滑程度常不能满足物理问题的需要。
(3)样条插值可以同时解决这二个问题,其基本思想是:把整个区间分段,各段分别用低次多项式来逼近一个函数,使整个函数成“装配式”,同时保证接缝(结点)处具有一定程度的光滑性(直到若干阶导数为连续)[11]。这样既可避免高次插值所具有的数值不稳定的龙格现象,又可避免一般的分段插值所导致的插值曲线不光滑的缺点。
因此,样条插值这种分段低次插值能够以低代价而获得较好的效果,在那些要求较高光滑性和收敛性条件的逼近问题中具有重要意义。
B样条曲线是贝塞尔(Bézier)曲线的拓广,与贝塞尔曲线相比,其突出优点是对局部的修改,不会引起样条形状变化的远距离传播,能够更好地实现曲线形状的局部控制。也就是说,在修改样条的某些部份时,不会过多地影响曲线到其它部份[12]。
k次B样条函数φk是分段k次多项式,其在(-∞,+∞)区间内的定义为:


其中的值可由式(6)来定义。

k次B样条函数φk的k-1阶导数连续,其中k阶导数的间断点为:
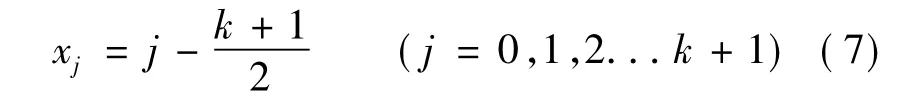
x0、x1、…、xk+1也是k次B样条函数φk的节点。φk虽然在整个实数轴(-∞,+∞)上都有定义,但在区间[x0,xk+1],即之外,其值恒为零。
在三维情况下,B样条函数具有自变量独立的性质,将x、y和z三个方向的B样条函数相乘,就可以得到三维B样条函数的表达式(8)。

三维B样条函数构成四维空间一个曲面体(见图1)。图1为三维三次B样条函数分别在x=0、y=0和z=0三个平面的切片示意图。

图1 三维B样条函数在x=0、y=0和z=0三个平面的切片Fig.1 Slices of 3D cubic B-spline function at x=0,y=0,z=0 respectively
实际上,三维B样条函数在y方向、z方向上的切片,与相应位置上x方向的切片在形态上是完全一致的,这是因为三维B样条函数本身的构建,就是由相互独立的三个方向的一维B样条函数相乘而来的,具有x、y、z三个自变量独立的性质。而且每一个平面切面的形态,类似于二维B样条函数。同时在x=-1平面的切片和x=1平面的切片,在形态上是完全一致的,这是因为每一个独立的一维B样条函数都是偶函数,这样相乘而来的三维B样条函数,具有分别关于x=0、y=0和z=0三个平面对称的性质。
在插值和曲面拟合时,使用次数越高的B样条函数,其相对误差越小。但这并不是说B样条函数的次数越高,其压缩拟合效果就越好。因为样条次数越高,其计算量越大,高次幂计算的截断误差也越大,这在边界上容易出现激烈抖动现象,从而造成边界点的相对误差较大。事实上,三次B样条函数插值和曲面拟合的效果已经很好,能够满足计算精度。三次B样条最高幂次为三次,在每一区间上振动不太大,连接点处具有二级光滑程度,这保证了根据实际问题设置的端点控制的计算稳定性。因此,作者选用三次B样条函数对走时表数据进行拟合。
2.2 曲面体拟合
如图2(见下页)所示,设已知N个散乱数据点f(xk,yk,zk)在x、y、z三个方向上的网格节点数目分别为Xres、Yres、Zres,这样就可以用三维空间中的一个最小长方体区域Ω={(x,y,z)|0≤x≤Xres,0≤y≤Yres,0≤z≤Zres}(图2中的小长方体)来描述这些散乱数据点集在三维立体中的投影区域。

图2 三维三次B样条函数插值示意图Fig.2 3D cubic B-spline function interpolation schematic
为了逼近散乱点集,构造一个连续均匀的三维三次B样条曲面体,这一曲面体由覆盖在矩形区域Ω上的控制顶点网格D(图2中外面的大长方体)来描述。为了消除边界因素地影响,分别向四周扩展了二个网格单位的边界。因此,D为共包含(Xres+4)*(Yres+4)*(Zres+4)个控制点的网格,且所有控制点均落在矩形域中的整数网格上。将每一个网格控制点的值表示为Cijl,其中i、j、l分别为x、y、z三个方向的序号,并且i=-1、0、…、Xres+2;j=-1、0、…、Yres+2;l=-1,0,…,Zres+2。因为所有的散乱数据点都落在Ω中,所以只要计算出D上的三维三次B样条曲面体控制点网格的值,就可以用插值方法来逼近数据点,集中的所有散乱数据。
因为三次样条函数的值不为零的定义域为(-2,2),受其限制,每一个散乱数据点最多由其相邻的5*5*5个控制点网格唯一确定,其余控制点网格的贡献为0。因此,一个散乱数据点的线性插值公式可简化为式(9)。

其中 φ(xk-xi)、φ(yk-yj)、φ(zk-zl)分别为x、y、z三个方向的插值基函数,即三次B样条函数。式(9)是一个欠定方程,有许多组Cijl满足式(9)的要求。为了得到Cijl点的值,可以构造如下最小平方目标函数Obj,设其为Cijl点对函数f在点(xk,yk,zk)处的真实贡献与期望值之差的平方和:

为得到最佳拟合参数Cijl(共(Xres+4)(Yres+4)(Zres+4)个参数),令这个目标函数最小,即令其对Cijl的偏导数为零:

这样即得到一个(Xres+4)(Yres+4)(Zres+4)阶线性方程组,求解此线性方程组,就可得到规则控制网格点的Cijl。再根据式(9)就可计算出各散乱数据点的值f(xk,yk,zk),甚至可估算出原来没有数值的点的值。只需存储有限个规则控制网格点的Cijl数据,就代表了原有许多散乱走时点,达到了散乱走时数据曲面拟合和压缩的目的。
3 走时数据存储
如前所述,每一个散乱数据点最多可由其相邻的5*5*5个控制点网格唯一确定,其余控制点网格的贡献为0。因此,当对式(10)中某一个Cijl求偏导数时,并不是所有控制点网格Cijl都参与计算,最多只有其周围的5*5*5个Cijl参与计算。这样在由一系列式(11)组成的线性方程组Ax=b中,每一个方程都有(Xres+4)(Yres+4)(Zres+4)个Cijl,但最多只有25组共125个Cijl的系数不为零。因此,系数矩阵A实际上是一个稀疏矩阵,具有25个条带的带状结构,每一个条带的带宽为5,如图3所示。

图3 三维走时数据曲面拟合的系数矩阵Fig.3 Coefficientmatrix of3D travel time data surface fitting
在图3中,外围的虚线是对扩展二个单位边界的网格点求偏导数的系数,这些系数中有些可能值不为零,有些可能整个一行值都为零或者是很小的值,这样就可能造成系数矩阵A不满秩。为了保证系数矩阵A满秩,同时保证线性方程组A x=b有稳定的解,所以在求解之前,需要在稀疏矩阵A的主对角线加上一个较小的阻尼,比如0.000 001。
为了能够利用较少的存储器空间储存稀疏矩阵完整的数据,通常采用压缩存储的方法,即不存储或尽量少存储稀疏矩阵的零元素,同时给出必要的索引信息,以便可以方便地找到所要用的非零元素在矩阵中的位置。当运算过程中产生新的非零元素时,有位置能方便地将其填入。
本算法选用CSC(Compressed Sparse Colum)存储法来存储如图3所示的稀疏矩阵A,该方法是对稀疏矩阵进行逐列压缩存储。为了存储n阶矩阵A,假设矩阵A中共有l个非零元素,则需要一个数据类型与矩阵A相同的l维向量x,按照先列后行的顺序,依次存放矩阵A中的非零元素;然后用一个整形的l维向量x(I),按照同样的顺序依次存放矩阵A中这些非零元素的行号;最后还需要引入一个n+1维的整形向量x(R),来指明矩阵A中第i列中第一个非零元素被存储在向量x中的位置。
本算法在求解稀疏矩阵线性方程组时,采用非对称的多波前法。即对于线性方程组Ax=b,通过矩阵A的LU分解来得到最后的解向量。多波前法(Multifrontal)是求解稀疏矩阵的比较稳定和高效的算法。其原理是找出并构造稀疏矩阵中的密集子块(Frontal),Frontal的分解直接调用BLAS(Basic Linear Algebra Subprograms)[13~15]。Frontal的生成、消去、装配、释放等,都是由特定的数据结构来指引。多波前法只存储非零元素的数值和位置,存储效率较高。在同一个波前,不管含多少列,其结构都是类似的。因此只需记录最左边那列的位置信息,其它列共用这些信息。波前越宽,节省的空间越多。而索引存储,链接表存储等,都要记录每列非零元素的数值和位置,因此效率要低于多波前法。
4 实际资料算例
为了验证本文方法的可行性,作者首先用三次B样条函数最小二乘法曲面拟合算法,对实际三维地震射线追踪走时表进行压缩;然后将规则网格控制点的数值存储入内存,以代表原有的散乱走时数据;最后在克希霍夫偏移成像时,直接在内存中对压缩后的走时表进行插值解编即可用于成像计算。
如图4(a)、图4(b)、图4(c)分别是中国西部某地区三维射线追踪走时表,在x、y和z三个方向上的三个切片示意图。原始走时表共有756 939个走时数据,使用三次B样条函数拟合压缩后,用14*14*14个网格点来表示。图4(d)为拟合相对误差分析,可以看出,拟合的相对误差绝对值最大不超过0.001,大多数点的拟合误差绝对值小于0.000 2,满足精度的要求。图4(e)是由原始走时表得到的克希霍夫偏移结果在主测线方向的一个切片;图4(f)是由压缩走时表方法得到的相同数据体的克希霍夫偏移切片。二种不同的走时数据调用方法得到的偏移结果差别不大,都能对重要构造进行很好地成像,并且都具有较小的偏移噪音。这说明压缩走时表对偏移结果精度的影响可以忽略不计。
通过算例可以看出,采用三次B样条函数拟合方法,对三维射线追踪走时表压缩具有较高的压缩比。同时,通过合理地规划规则网格节点,可以保证压缩拟合的计算效率和计算精度。把这些有限个规则网格控制点的数值存储于内存中,在偏移成像时,在内存中使用三次B样条函数的线性插值,即可解编出原有的散乱走时数据。由于省去了频繁读取大数据量的走时表文件,所以克希霍夫偏移成像的计算效率提高了二倍以上。此外,由于走时表压缩和解编的计算精度都很高,所以通过压缩走时表来得到的偏移结果,与常规的直接读取走时表文件得到的偏移结果相比,具有很高的逼近程度。
关于压缩比例需要说明的是,根据Nyquist采样定律,当采样频率fs不小于信号中最高频率fmax的二倍,即fs≥2fmax时,离散信号采样能无失真地恢复到原来的连续信号。一般在实际应用中,应保证采样频率为信号最高频率的5倍~10倍才能保证合理的精度。由理论模型分析可得,一个周期至少需要十个左右的规则网格点,才能保证拟合相对误差的精度。比如对于一个模型,模型数据波动大约1.33个周期,用大于14*14*14的三维规则网格点去拟合压缩,数据波动在三个方向的每个周期中,大约有14/1.33≈10个规则网格点,这样的拟合压缩是合适的。如果数据波动的每个周期中的规则网格点数小于10,这样的拟合压缩则不能保证合理的精度,自然是不合适的。

图4 压缩走时表偏移实例Fig.4 Migration example by compressing travel time data
5 结论
地震波走时是克希霍夫叠前深度偏移的必要参数,在偏移过程中需频繁调用各成像点的走时数据。但是,由于三维射线追踪的走时表属于大型散乱数据,现有的克希霍夫偏移成像方法是将走时表作为文件来存储。由于需要频繁读取大数据量的走时表文件,所以计算效率不尽人意。为了提高克希霍夫偏移成像的计算效率,而不至于对计算精度造成不利影响,作者在本文中采用了一种先对三维射线追踪走时表进行压缩,再利用压缩后的走时数据进行偏移的方法。具体做法是:首先规划一个具有规则网格控制点,并包含所有散乱数据点集的最小盛放区域;然后利用三次B样条函数,对散乱的走时数据进行最小二乘曲面拟合,从而求出各规则网格控制点的数值;最后只需要把这些有限个规则网格控制点的数值,以数组形式存储于内存中。在偏移成像时,再由这些规则网格控制点的数值,使用B样条函数的线性插值公式解编出走时表。
在计算时充分考虑本算法最小二乘法线性方程组的系数矩阵为稀疏矩阵,并且具有非零元素规则排列的特征。因此为了进一步节省内存空间,同时提高存储效率,在矩阵存储时作者采用了稀疏矩阵存储方法,并使用基于多波前法的LU分解求解稀疏矩阵线性方程组。实际地震资料算例验证了本三维走时表压缩算法的可行性,计算的快速性以及控制节点的稳定性。对射线追踪走时表进行科学合理的压缩存储,省去了频繁地进行大数据量文件的读写操作,促使三维克希霍夫偏移成像的计算效率提高了二倍以上,并且对偏移结果精度的影响还可以忽略不计。对射线追踪走时表进行的科学合理的压缩存储方法,可用于提高其它地震正演模拟,以及地震层析成像等的计算效率。
[1]郭洪升,陈俊良.地震数据实时自适应压缩方法研究[J].地震学报,1989,11(1):68.
[2]张军华,仝兆岐.用小波变换法定量压缩地震数据[J].石油大学学报:自然科学版 ,2003,27(5):29.
[3]王喜珍,滕云田,高孟潭,等.基于整数小波变换的地震数据压缩[J].地震学报,2004,26(增刊):116.
[4]余平,马小虎,陈恒金.基于提升小波的地震数据压缩编码算法[J].苏州大学学报:工科版,2009,29(1):7.
[5]AVERBUCH A Z,METER F,STROMBERG J O,et al.Vassiliou,Low bit-rate efficient compression for seismic data[J].Institute of Electrical and Electronics Engineers Transactions on Image Processing,2001,10:1801.
[6]BERNASCONIG,VASSALLO M.Efficient data compression for seismic-while-drilling applications[J].IEEE Transactions on Geoscience and Remote Sensing,2003,41:687.
[7]WU R S,WANG Y.Seismic data compression using adapted local cosine transform and its effect on imaging,61st Meeting[E].European Association of Geoscientists and Engineers,Extended Abstracts,2003.
[8]GIANCARLO B,VITTORIO R.High-quality compression of MWD signals[J].Geophysics,2004,69:849.
[9]CABDèSE J,DEMANET L.The curvelet representation of wave propagators is optimally sparse[J].Communications on Pure and Applied Mathematics,2005,58:1472.
[10]CHENG G,ZHANG B.Compression storage and solution of large sparse matrix[J].Progress in Geophysics,2008,23:674.
[11]关履泰,覃廉,张健.用参数样条插值挖补方法进行大规模散乱数据曲面造型[J].计算机辅助设计与图形学学报,2006,18(3):372.
[12]毛可飞,路辉.基于多层B样条的海底地形生成方法[J].计算机仿真,2005,22(4):222.
[13]夏爱生,胡宝安,申楠公,等.系数矩阵为带状大型稀疏矩阵线性方程组解法研究[J].军事交通学院学报,2007,9(1):83.
[14]成谷,张宝金.反射地震走时层析成像中的大型稀疏矩阵压缩存储和求解[J].地球物理学进展,2008,23(3):674.
[15]陈英时,吴文勇.采用多波前法求解大型结构方程组[J].建筑结构,2007,2(9):138.
P 631.4
A
1001—1749(2011)02—0122—07
教育部高等教育博士点专项研究基金资助(200804251502);中国石油天然气集团公司创新基金资助(07E1019);中央高校基本科研业务费专项资金资助(09CX04013A)
2010-09-10改回日期:2010-12-13
王珺(1973-),女,山东东营人,博士,讲师,现于中国石油大学信息与控制工程学院任教。
