基于单程波真振幅分步傅里叶叠前深度偏移方法
2011-10-17解建建王绪本
解建建,王绪本
(成都理工大学 地球探测与信息技术教育部重点实验室,四川成都 610059)
基于单程波真振幅分步傅里叶叠前深度偏移方法
解建建,王绪本
(成都理工大学 地球探测与信息技术教育部重点实验室,四川成都 610059)
这里将单程波真振幅方程与分步傅里叶算子(SSF)相结合,同时还结合了保幅算法和分步傅里叶算法的优点,因此该方法具有计算量小,占内存少,能处理横向变化的速度等优点。并且克服了傅里叶有限差分方法偏移后的振幅都有很大的偏差的不足。与目前广泛应用的常规的分步有限差分叠前深度偏移相比,具有成像精度高,保持地震波动力学特征等优点。在M armousi模型上成功地进行了真振幅分步傅里叠前深度偏移处理,取得了理想的成像效果。
单程波动方程;真振幅;分步傅里叶算子;叠前深度偏移
0 前言
为了得到较好的成像效果,人们致力于研究基于波场延拓理论的波动方程叠前深度偏移算法。根据采用的波场延拓算子的不同,近年来研制出的波动方程叠前深度偏移算法有多种:运用波数~频率域的相移法;相移加插值PSPI[1]算法;分步傅氏SSF算法[2];频率~空间域的有限差分FD算法等[3]。在成像过程中,相移法和有限差分算法各有优缺点。分步傅立叶偏移方法在处理速度横向变化的能力与计算效率等方面,较之“相移加插值”方法明显存在优势。该方法的地震成像没有倾角限制,但对复杂地质体(如超覆、逆掩断层、盐丘等)成像,其内部速度场横向变化非常剧烈,成像的误差非常大。严格地说,相移法只适用于垂向速度变化,不允许速度的横向变化。由于分步傅立叶方法没有考虑速度场二阶以上的扰动,因此,它很难使复杂地质体正确成像。有限差分算法能够保持地震波的动力学特征,允许速度的任意变化,但存在偏移角度的限制。那么,如何才能有一种高计算效率,且成像精度高的偏移算法呢?
最近几年来,人们都是在原有方法的基础上,在提高计算效率和保幅方面做进一步研究。作者在本文依赖传统的SSF偏移算子高计算效率的优势,提出了基于单程波方程的真振幅分步傅里叶偏移算法,这样既提高了计算效率,又解决了SSF算子在强横向介质中不适应的问题,并通过M armousi模型试算来验证了此算法。
1 真振幅分步傅里叶偏移原理
1.1 单程波方程
张关泉[4]证明了光滑不均匀介质中,全声波方程近似为
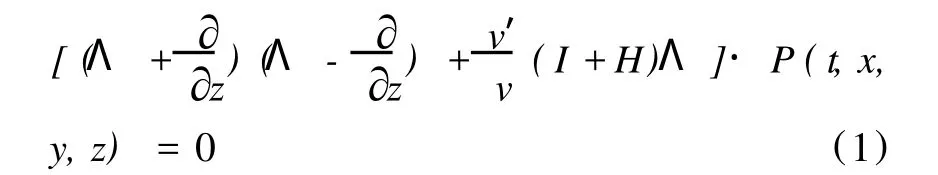
并由此提出了下面的单程波分解方程:
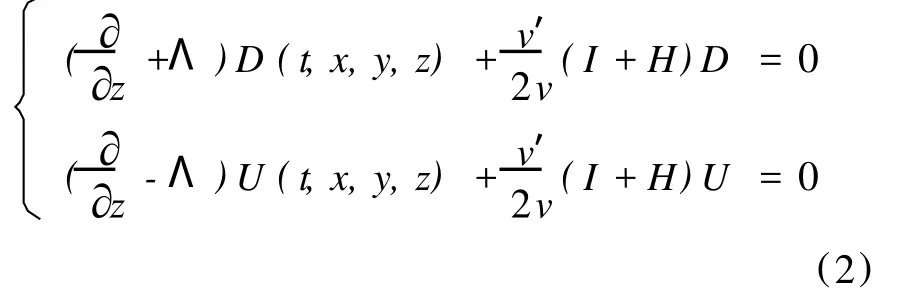
为了实现真振幅共炮偏移,张宇[5]提出了单程波方程和边界条件
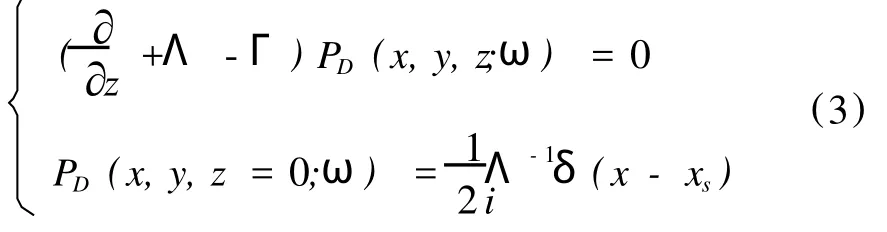
和
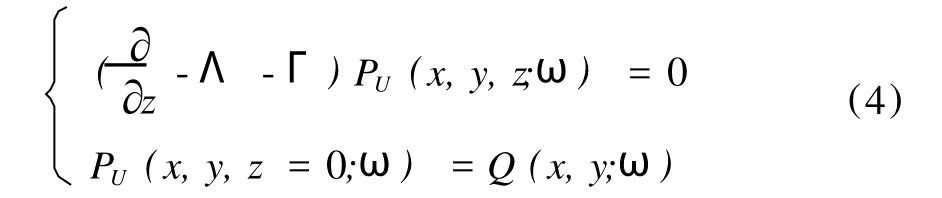
1.2 真振幅偏移算子
以上行波方程(3)为例:
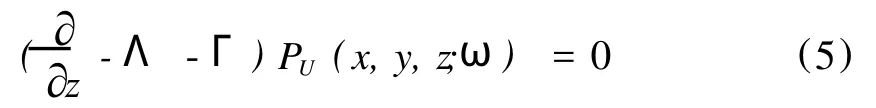
(1)以参考速度做相移法。在空间频率域中方程(5)分二步实现:
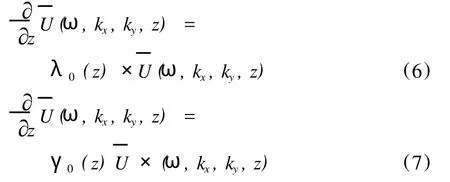
其中 kx、ky分别为x、y方向的空间波数;v0(z)为随深度变化的参考速度。
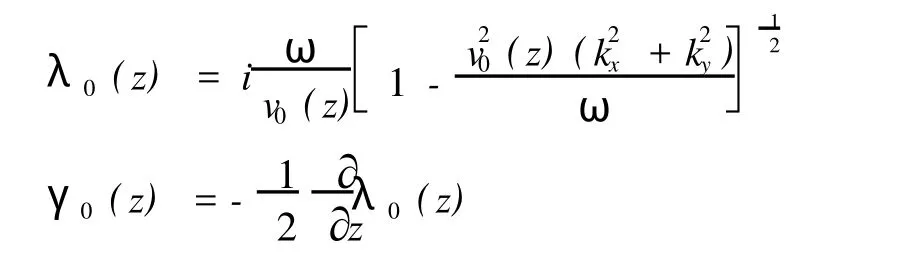
方程(6)的求解可以写成:
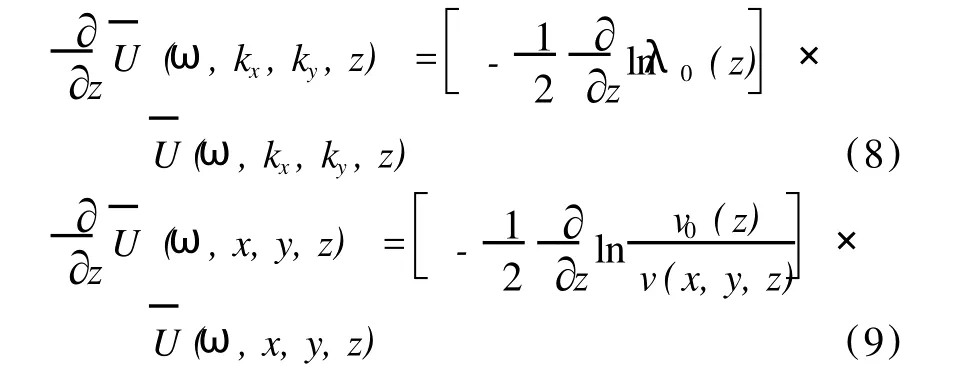
式(8)为变量z的常微分方程,经求解可得:
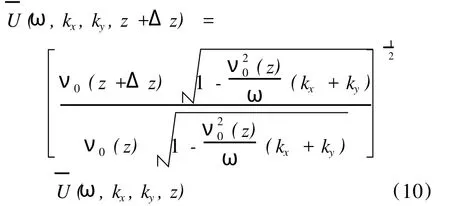
(2)薄镜校正项。求解该常微分方程(9)得到:
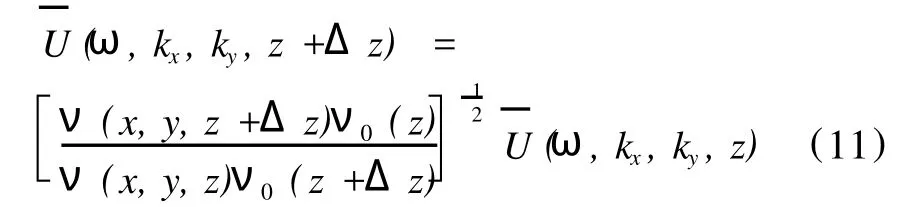
为了得到正确的偏移振幅,在偏移之前必须进行球面扩散校正。式(10)和式(11)就是在SSF的基础上,针对散射项所做的偏移算子,能够正确地显示出振幅的信息。
2 模型试算
为了验证本文中方法的保幅性,首先我们设计了一个简单的2D凹槽模型。图1是用传统SSF偏移成像剖面,可见能够给出正确的成像位置,但是该方法对构造成像而言精度比较低。

图1 传统SSF偏移成像Fig.1 Trad itional SSFm igration im aging
图2为真振幅SSF偏移成像剖面,它不但给出了正确的成像位置,而且整张剖面的成像振幅比较均衡。该方法对于倾斜界面和最下面的平层的成像,比传统SSF方法的成像效果好,精度更高,而且对构造成像更加清晰,这说明该方法能有效处理强间断速度变化。
作者在文中用M armousi模型验证该方法,能够有效地解决复杂地质模型。M armousi模型构造复杂,存在剧烈的横向变速,因此M armousi模型是国际公认的检验叠前深度偏移方法的理想模型。图3是M armousi模型速度场,这里所采用的数据集的参数为:共有240个炮集,每炮96道,炮间距25m,道间距25m,采样率4m s。下页图4是在准确的速度模型下,用传统的SSF叠前深度偏移成像的结果。下页图5是在准确的速度模型下,得到的真振幅SSF叠前深度偏移成像的结果。从二者的对比中可以更加明显地看出,真振幅SSF偏移成像的结果中模型浅层的三个大的断层,以及中深层的背斜和低速体等构造形态,都能够得到更好的体现,刻画出了波场随速度场变化的细节,整个偏移剖面具有质量很高的成像效果。通过以上针对M armousi模型的偏移成像结果的对比,可以看出与传统SSF偏移算子相比,真振幅SSF偏移算子的优势所在。
3 结论
真振幅SSF偏移是基于传统的SSF的一种偏移方法,通过对凹槽模型和M armousi模型的多个炮点的偏移成像结果对比,真振幅SSF叠前深度偏移方法是实现较复杂地质构造成像的一种快速有效的方法,它解决了传统SSF方法不能保证实现保幅偏移成像的缺点,在提高计算效率的同时,也加强了速度场横向变化的适应性。在降低计算量和提高成像质量方面将会有很大的优越性。
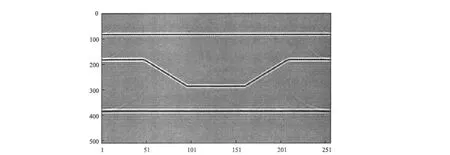
图2 真振幅SSF偏移成像Fig.2 True amp litude SSFm igration im aging
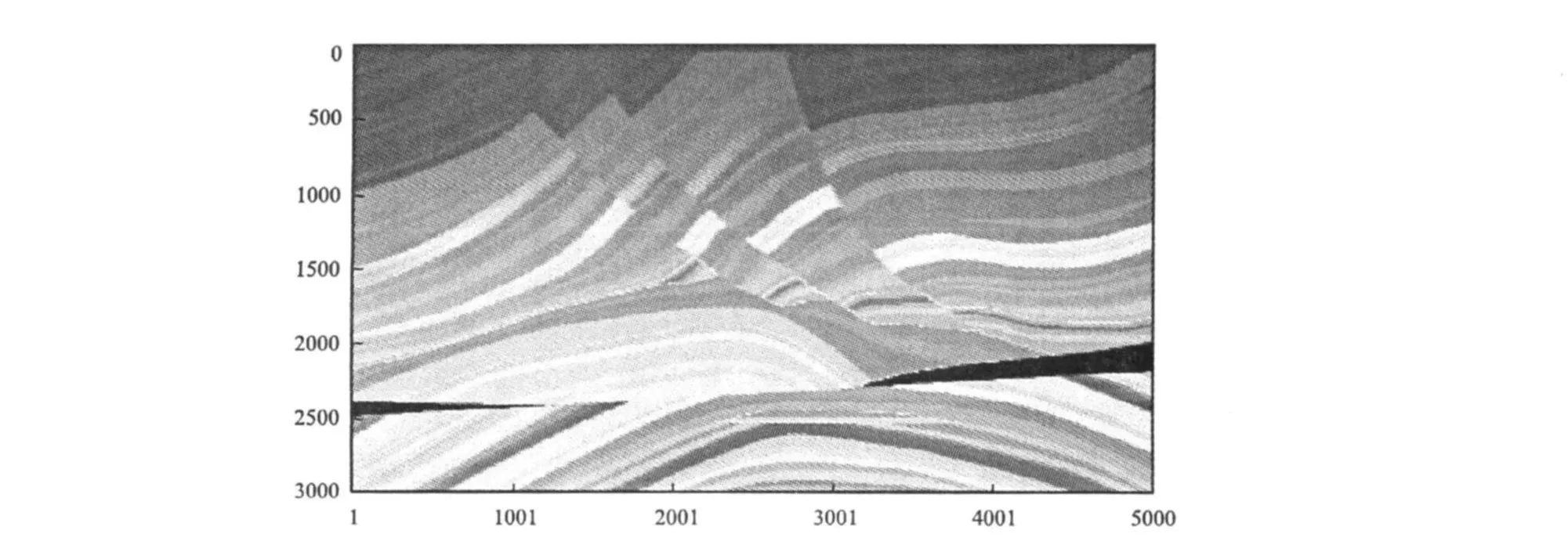
图3 M armousi模型速度场Fig.3 Velocity field ofM armousimodel
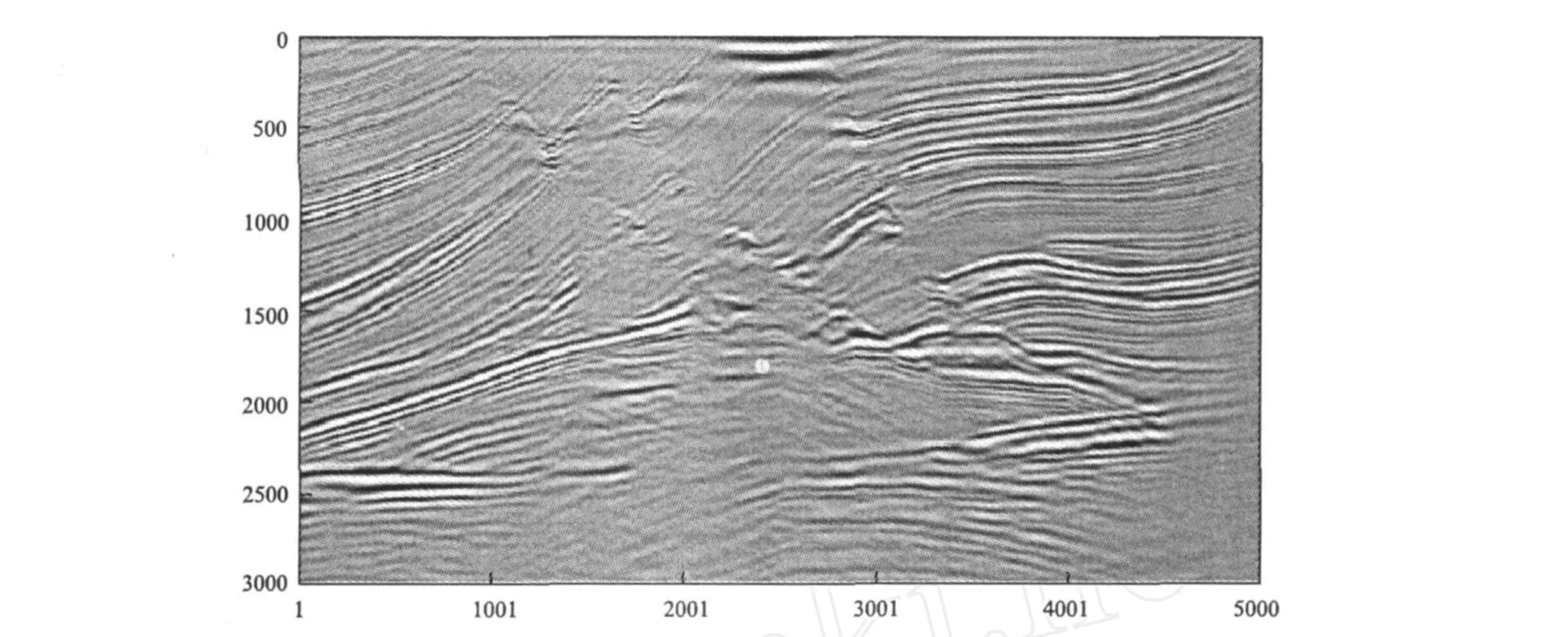
图4 M armousi模型传统的SSF偏移成像结果Fig.4 Traditional SSFm igration im aging ofM armousimodel

图5 M armousi模型真振幅SSF偏移成像结果Fig.5 True amp litude SSFm igration im aging ofM armousimodel
[1]GAZDAG J.W ave equationm igration w ith the phaseshiftm ethod[J].Geophysics,1978,(43):1342.
[2]STOFFA P L,FORKEMA J T,DE LUNA FRE~RE.ETC.Sp ilt-step Fourierm igration[J].Geophsics,1990,55(2):410.
[3]R ISTOW D.RUH 1 T.Fourier finite-differencem igration[J].Geophysic,1994,59(12):1822.
[4]张关泉.波动方程的上行波和下行波的耦合方程组[J].应用数学学报,1993,18(2):251.
[5]贺振华,王才经,李建朝,等.反射地震资料偏穆处理与反演方法[M].重庆:重庆大学出版社,1989.
[6]张宇.振幅保真的单程波方程偏移理论[J].地球物理学报,2006,49(5):1410.
[7]李振春,朱绪峰,韩文功,等.真振幅偏移方法综述[J].勘探地球物理进展,2008,2(31):12.
[8]崔兴福,张关泉,吴雅丽.三维非均匀介质中保幅地震偏移算子研究[J].地球物理学报,2004,47(3):509.
[9]贺振华,王才经,李建朝,等.反射地震资料偏移处理与反演方法[M].重庆:重庆大学出版社,1989.
[10]张宇,徐升,张关泉.等.真振幅全倾角单程波方程偏移方法[J].石油物探,2007,46(6):582.
[11]吕彬,王宇超,李斐,等.保幅型裂步傅里叶叠前深度偏移方法探讨[J].岩性油气藏,2007,19(3):101.
[12]董伟,徐兆涛,分步傅立叶波动方程三维叠前深度偏移算法及应用[J].油气地质与采收率,2008,(增刊):16.
P 631.4
A
1001—1749(2011)01—0036—04
2010-07-26 改回日期:2010-11-01
解建建(1985-),女,硕士,现主要从事波动方程偏移成像方面的研究。
