工件排序的改进蚁群算法优化

王欣盛, 马 良

(上海理工大学管理学院)

工件排序的改进蚁群算法优化

王欣盛, 马 良

(上海理工大学管理学院)

就工件排序问题中的一种类型设计了融合局部改进策略的蚁群算法进行求解,并用Delphi在计算机上实现了相应的算法软件.经大量算例测试,获得了较好的效果,验证了算法的可行性和有效性.

排序问题;蚁群算法;组合优化

工件排序问题[1]是组合优化中的著名难题,由于其一般情形下的NP(nondeterminstic polynomial)难解性,人们一直在不断地对其进行研究.而排序问题在现实中的应用,如航班着陆排序、汽车组装线排序等,更是对人们的日常生活和工作有着重大的影响.

自20世纪90年代以后,来自自然界的仿生类算法开始引起人们的关注,尤其是在解决组合优化难题方面,得到了一系列的尝试和深入研究.其中,源自生物世界的蚁群算法在近十几年里获得了长足的发展[2-9].

本文主要针对一类工件排序问题设计了一种改进的蚁群算法,并在计算机上实现了相应的软件程序,经大量算例测试,获得了较好的效果.

1 问题概述

考虑单工序、多品种、多机器工件加工排序问题,即有多个品种的工件,其中,每个工件只有一道加工工序,众多工件同时在多台加工机器上并行加工,具体描述为:

有x件工件,y台不同种类的机器,每个工件可以在任何一台机器上加工,第i件工件在第j台机器上的加工时间为t ij,U={U1,U2,…,U y},U是在第i台机器上所有加工工件的集合,优化的目标是使各台机器上的最大加工时间值最小.

2 基于蚁群算法的改进

2.1 算法改进思想

现介绍有关概念的定义.

节点:每个节点代表两个实体---加工机器和工件,有M*N个节点,其含义为第i个工件在第j个机器上加工.

边与边长:蚁群算法在处理此类型工件排序问题上,可忽略边的存在,转而关注从节点到节点转移所花费的时间.若要从某个节点转移到另一节点,需要花费的时间可以在目标节点中获得,即从节点i转移到节点j所需要的时间为节点j(节点j是由第x个工件与第y台机器组合而成)第x个工件在第y台机器的加工时间.

蚂蚁:在众多的节点中转移,通过其转移到的节点,来确定工件排序的可行解,并且通过对可行解的比较,得出问题的最优解.

2.2 算法改进关键点

对基本蚁群算法作如下改进:

a.将待加工工件与加工机器的组合作为蚁群算法中每个蚂蚁所要转移的节点.

b.将工件加工时间作为蚂蚁在节点转移中所花费的时间,该时间与所要转移的节点有关,即节点为第i个工件在第j台机器加工,则转移所需花费的时间为第i个工件在第j台机器加工的时间.

c.转移概率结合考虑转移花费时间与其他蚂蚁留下的信息素浓度.

d.解是由M(机器台数)个子解集构成,每个解集代表在该台机器加工的工件号.

e.每次循环后(即同一时刻出发的蚂蚁全部完成觅食后),对信息素进行更新.

2.3 改进蚁群算法描述

首先随机放置m个蚂蚁到n个节点上,然后对每个蚂蚁进行节点转移.在蚂蚁要选择一个节点作为移动目标前,按转移概率选择可能转移的节点.蚂蚁转移的可能性为轨迹强度的增函数、花费时间的减函数,即转移花费时间越少,可见度越大,越容易被选择;而走过的蚂蚁越多,在边上留下的轨迹信息素越多,轨迹强度就越强,也越容易被选择.经多次循环后,所有的蚂蚁所走的路线趋向于最佳路径.

由于这里研究的是单工序、多工件、多机器的加工工件排序问题,其解的形式不同于双机N件工件排序问题的解形式,最终所得的解是由M个(加工机器数)子解集的集合,每个子解集的值代表在该加工机器上需要加工的工件号.

3 改进蚁群算法规则及步骤

在原始蚁群算法规则和步骤基础上,即可实现具体的改进蚁群算法

3.1 相关参数

α为信息素相对重要性,α≥0;β为转移时间相对重要性,β≥0;ρ为轨迹衰减度,0≤ρ≤1;τ为信息素,τ≥0;m为蚂蚁数,m≥0;U i为第i台机器加工的工件集合;S i为集合的U i未来总加工时间,Si≥0;Q为蚂蚁一次所留信息素的量为一个常数;d为节点转移所需时间;η为节点能见度,等于1/d;θ为某机器未来加工总时间的相对重要度,θ≥0;P为转移概率;p kse为第k只蚂蚁从节点s转移到节点e的转移概率;s,e分别为所在节点,转移目标节点;Δτij为节点i到j的信息素增量;d ij为第i个工件在第j个机器加工时间.

3.2 目标函数

3.3 规则

3.3.1 状态转移规则

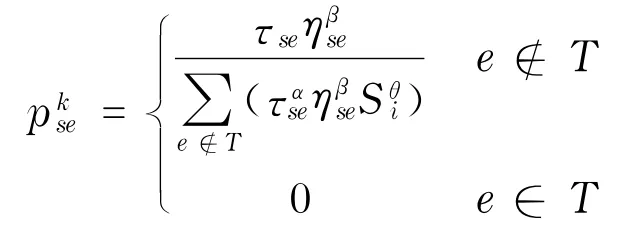
当转移目标节点e不在禁忌表T中,计算转移概率;如果该点在T中,则不考虑转移到该节点.当p k

se=0时,直接将其视为最佳转移概率.如果有相同转移概率的节点存在,则从中随机选取一个作为转移节点.其中,i与e节点的加工机器号相等.

3.3.2 轨迹强度更新规则

在蚁群算法中,第k只蚂蚁从节点s到节点e的转移路径所留下的信息素,可由有该蚂蚁觅食的时间来决定,故该蚂蚁在从s节点转移到e节点所留下的信息素为

同一时刻出发的蚂蚁全部完成觅食(找到可行解)后,轨迹强度更新规则为

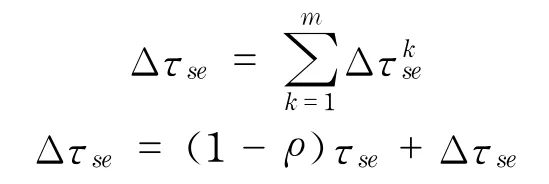
3.4 算法步骤

步骤1初始化.初始化各个节点的信息素,赋值为0;T表(禁忌表)初始化,置空;随机将m个蚂蚁放置于n个节点上;将路径信息素赋初值,这里使用Q/(min加工时间×零件数).

步骤2将T表与U相对应,蚂蚁的初始出发点置于T表中,同时给相对应的U i集合添加该工件号.

步骤3对每个蚂蚁计算转移概率p krs,按最大转移概率将该蚂蚁从现节点转移至s节点,并将s节点放T表中,在相对应的U i集合添加该工件号.如所对应的U i为空,则将该工件号直接放入该子解集中;如不为空,则计算每个U i的所含有的元素的加工时间总和.选取加工时间总和最小的U i集合,放入所选节点的工件号,若有多个U i集合加工时间总和最小,则随机选取一个集合.

步骤4在蚂蚁获得可行解后,计算每个蚂蚁的目标函数值,在同一时刻出发的所有蚂蚁得到可行解后,作邻域搜索局部改进,并更新轨迹强度.

步骤5如循环次数达到或超过给定的最大循环次数,结束排序,输出当前最佳结果;否则,转步骤2.

4 改进蚁群算法的Delphi实现

整个算法用Delphi 10实现,并在Windows XP环境下运行通过.相应的算法软件界面如图1和图2所示.

算法软件可通过导入数据文件、手工输入或通过测试数据生成器来形成原始数据,并在软件的输入框中显示这些数据.在软件求解完毕后,会在右输出框中显示相应的结果.

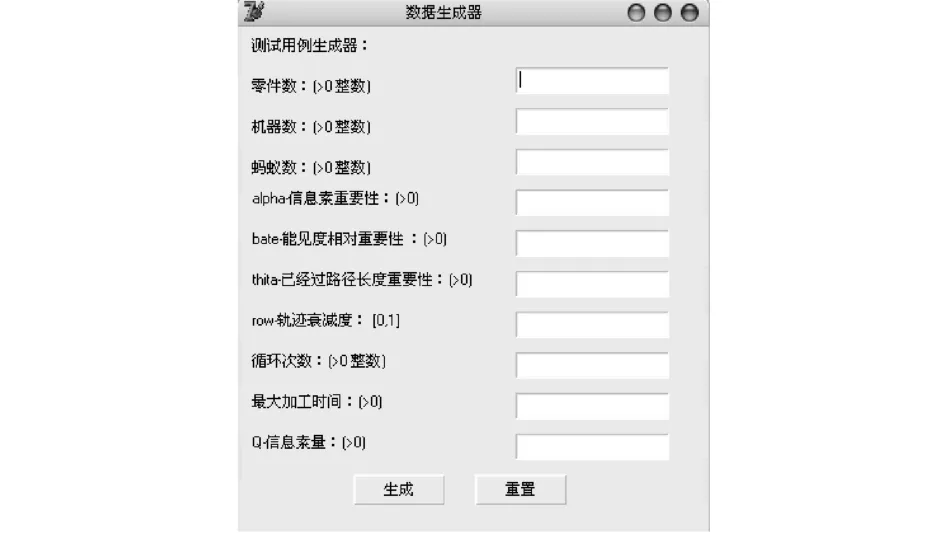
图1 测试用例生成器Fig.1 Test data generator

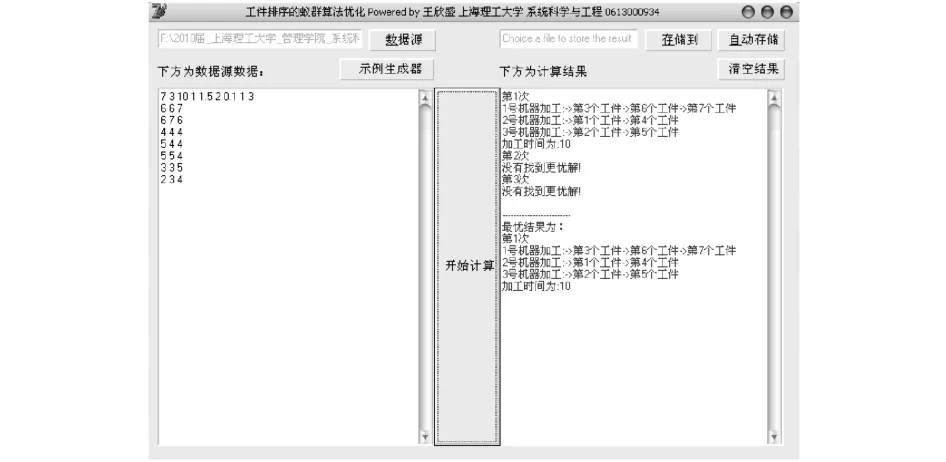
图2 软件计算示意图Fig.2 Software computation

5 算例测试

例1数据如表1所示.

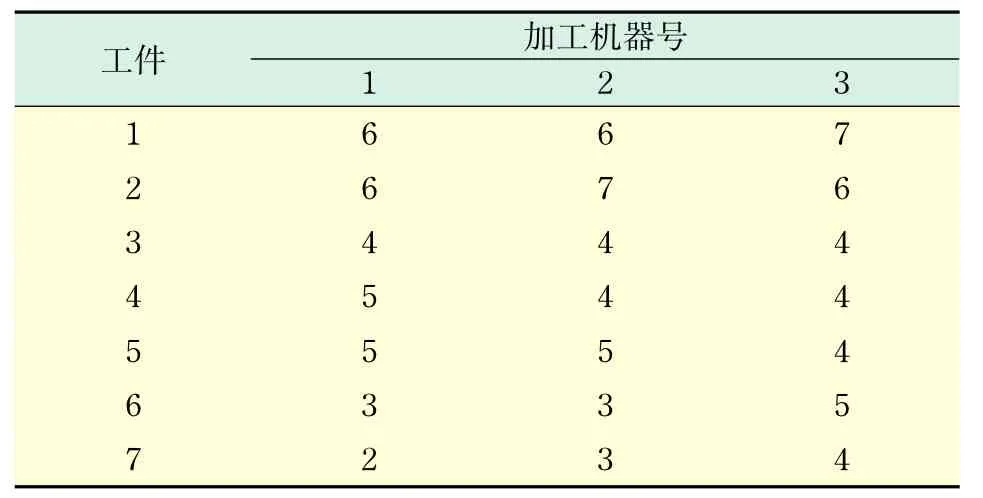
表1 算例数据1Tab.1 Sample data 1

在工件数为7,加工机器数为3,蚂蚁数量为10,能见度重要性为1.5,已经过路径长度重要性为2,轨迹衰减度为0.1,循环次数为50的情况下,所得计算结果如表2所示.

优化结果为:

1号机器加工:→第5个工件→第6个工件→第7个工件(实际加工时间为10);

2号机器加工:→第1个工件→第4个工件(实际加工时间为10);

3号机器加工:→第2个工件→第3个工件(实际加工时间为10);

机器最大加工时间为10.

例2数据略.

在工件数为7,加工机器数为3,蚂蚁数量为20,能见度重要性为1.5,已经过路径长度重要性为2,轨迹衰减度为0.1,循环次数为80的情况下,所得计算结果如表3所示.机器最大加工时间为42.5.

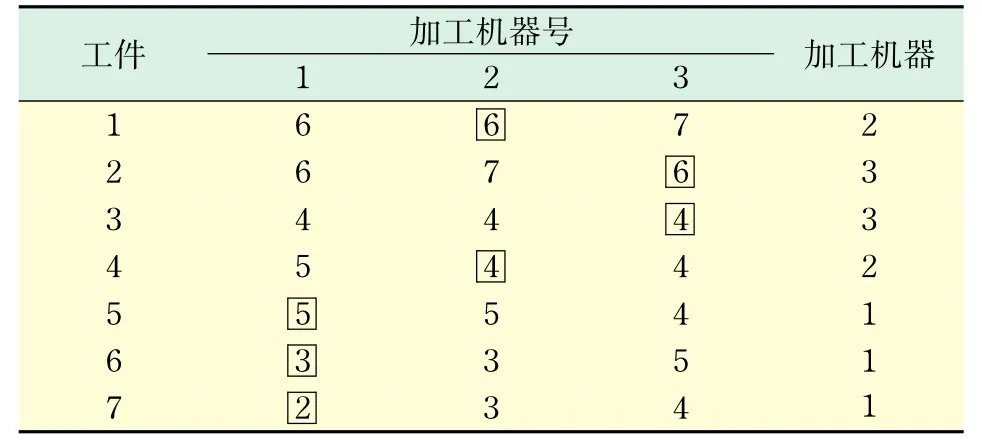
表2 计算结果1Tab.2 Computational results 1

表3 计算结果2Tab.3 Computational results 2

例3数据如表4所示.

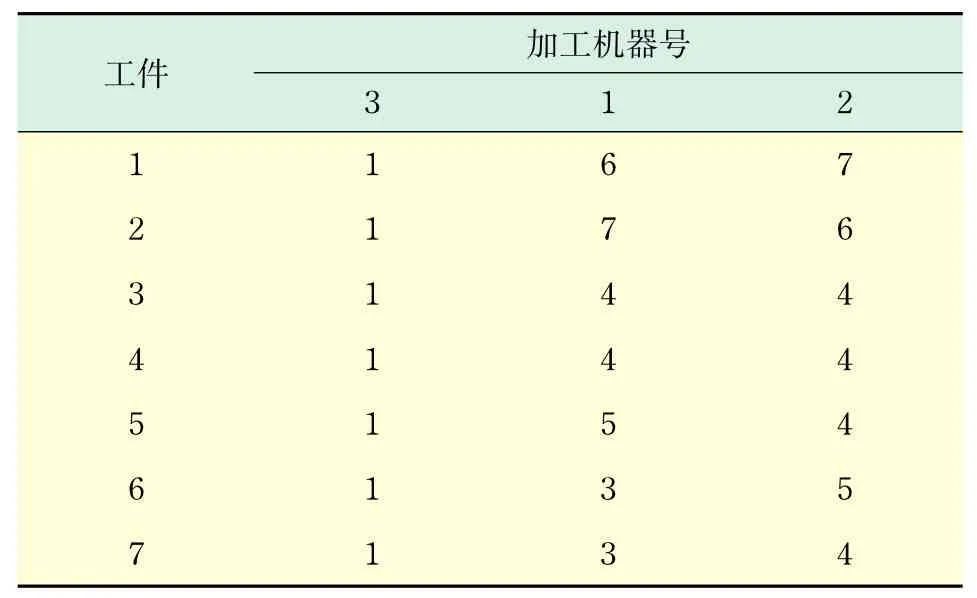
表4 算例数据3Tab.4 Sample data 3

在工件数为7,加工机器数为3,蚂蚁数量为10,能见度重要性为1.5,已经过路径长度重要性为2,轨迹衰减度为0.1,循环次数为50的情况下,所得计算结果如表5所示.

表5 计算结果3Tab.5 Computational results 3

最终结果为:

1号机器加工:→第1个工件→第2个工件→第5个工件→第6个工件→第7个工件(实际加工时间为5);

2号机器加工:→第4个工件(实际加工时间为4);

3号机器加工:→第3个工件(实际加工时间为4);

机器最大加工时间为5.

6 结束语

蚁群算法是一种仿生智能优化算法,在求解许多NP-难题中表现出了良好的性能.这种随机寻优方法具有很强的发展潜力,同时,还常常能与其他的优化算法相结合.本文仅对单工序、多工件、多加工机器的工件排序问题设计了相应的改进蚁群算法,并在计算机上予以实现,为实际问题的求解提供了方便的软件工具.

[1] 陈义保,姚建初,钟毅芳,等.基于蚁群系统的工件排序问题的一种新算法[J].系统工程学报,2002,10(5):476-480.

[2] 马良,王波.基础运筹学教程[M].北京:高等教育出版社,2006.

[3] 马良,朱刚,宁爱兵.蚁群优化算法[M].北京:科学出版社,2008.

[4] 雷德明,严新平.多目标智能优化算法及其应用[M].北京:科学出版社,2009.

[5] 王洪刚,马良.TSP的量子蚂蚁算法求解[J].运筹与管理,2009,18(6):11-13.

[6] 朱刚,马良,高岩.离散元胞蚂蚁算法及其收敛性[J].科学技术与工程,2009,9(5):1115-1119.

[7] 朱刚,马良.生长竞争型函数优化的蚁群算法[J].数学的实践与认识,2010,40(2):108-112.

[8] 朱刚,马良.多目标优化的生长竞争蚁群算法[J].系统工程,2010,28(12):91-95.

[9] 刘勇,马良.非线性0- 1规划的元胞蚁群算法[J].系统管理学报,2010,19(3):351-355.

Improved ant colony optimization for scheduling problem

WANGXin-sheng, MA Liang
(University of Shanghai for Science and Technology,Shanghai 200093,China)

Combined with the local searching strategy,an ant colony optimization algorithm was proposed for a kind of scheduling problems.The algorithm is coded in Delphi and runs on microcomputer.By solving series of experimental examples,the modified algorithm was tested and validated with satisfactory results achieved.The computational results prove the feasibility and effectiveness of the algorithm for solving scheduling problems.

scheduling problem;ant colony algorithm;sombinatorial optimization

O 22

A

1007-6735(2011)04-0362-05

2010-06-09

王欣盛(1988-),男,本科.研究方向:系统科学.E-mail:wangxsh42@126.com马 良(联系人),男,教授.研究方向:智能优化.E-mail:maliang@usst.edu.cn