多重分形序列的可见图分析

唐 镇, 王建勇, 杨会杰

(1.上海理工大学管理学院,上海 200093;2.邢台学院物理系,邢台 054001)

多重分形序列的可见图分析

唐 镇1, 王建勇2, 杨会杰1

(1.上海理工大学管理学院,上海 200093;2.邢台学院物理系,邢台 054001)

可见图方法将多重分形时间序列映射为相应的网络,研究并对比了由不同机制产生的多重分形序列的非平凡特征,发现单分形时间序列的简单叠加得到的混合序列有多分形性质,对应的可见图是无尺度网络;而通过模型产生的多分形序列对应的可见图一般不具有无标度性质.为了辨别不同机制生成的多分形时间序列,小波分析和可见图必须联合运用才能识别这两种不同的分形结构,可见图算法作为传统时间序列分析方法的补充在揭示序列产生机制时具有重要的用途.

可见图;多重分形时间序列;度分布

近年来一个长盛不衰的研究课题是将时间序列映射到复杂网络,从复杂网络这一全新的视角出发对时间序列进行分析,期望能够提取到新的序列结构特征,深入认识复杂系统的结构和动力学机制[1-9].其中,有广泛影响的是可见图方法[10].将时间序列的每个数据点映射为节点,从任意节点出发,将该节点“视野”内的其他节点与之相连,得到时间序列对应的可见图.这种网络能反映原时间序列的大部分性质,如周期、随机、分形序列分别转化为规则、随机和无标度网络.并且,可见图可以用于估算分数布朗运动的休斯特指数(Hurst exponent).可以证明,分数布朗运动的可见图的度分布满足幂律函数,幂律指数α与休斯特指数H满足线性函数关系[11],α=3-2H.可见图也被成功地应用于汇率序列[12]、心跳信号[13-14]等实证数据分析.

但是,现有文献的研究工作主要是基于理论模型产生的数据的分析.这些数据具有定态、单纯成分等良好的特性,这是实际数据不具备的.现实中大量的时间序列具有多分形的特征.很多序列是多个时间序列的混合,如股票综合指数、居民消费价格指数、信息流量纪录等.只有文献[15]考察了多重分形随机游走序列的可见图,发现这种机制生成的多分形的可见图也具有无尺度性质.本文考察和比较了采用不同形成机制产生的多分形的可见图的性质,发现单分形布朗运动叠加得到的混合序列同时具有多分形特征和无尺度性质,而多分形理论模型产生的序列一般不具有无尺度性质.因此,必须联合运用小波分析和可见图方法,才能发现不同种类的多分形序列背后产生机制的差异.一般情况下,需要通过分析复杂系统的输出序列来探测系统的动力学机制,因此,本文的结论具有重要的理论参考价值和潜在的应用价值.

本文首先介绍了可见图的概念,对单分形布朗运动的叠加进行小波和可见图分析,并与理论模型产生的多分形序列的可见图进行了比较,发现必须联合使用小波分析和可见图方法才能识别多分形序列的产生机制之间的差异.

1 方 法

1.1 可见图

可见图方法是由西班牙马德里理工大学Lacasa与Luque等人提出的关于将时间序列映射为相应网络的数学算法[10],该方法的优点不但保留了原有序列的大部分性质,而且通过研究网络参数可以提供更多关于有关序列的信息.先假设一标量序列为{y i|i=1,2,…,N},其中,N为记录序列的最大值.若对于两节点A(a,y a),B(b,y b)之间的任意节点C(c,y c)满足条件那么,节点A,B相连,或称其可见.如图1所示,因序列为标量序列,图中纵坐标为相应标量值.一般情况下,周期序列、随机序列、分形序列最终分别转化为规则网络、随机网络和无标度网络.

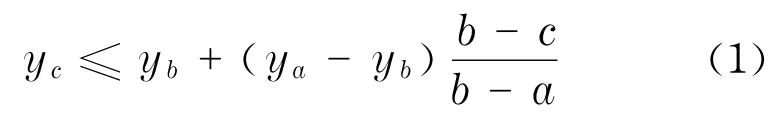
图1 可见图构造算法示意图Fig.1 Illustration for the algorithm of visibility graph

1.2 多分形谱

采用小波变换探测序列的标度性质[16].时间序列{y i|i=1,2,…,N}的小波变换可以写为

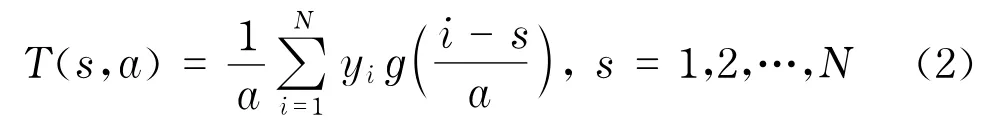
式中,g(·)为小波函数;a为小波变换窗口尺度;s为序列中的元素编号.

时间序列的多分形指该序列能够分解为具有不同局域休斯特指数的子集,也就是具有不同的局域奇异性特征.找出上述小波变换T(s,a)序列的极大值集合T(s,a),s=s1,s2,…,s M,其中,s是序列的极大值对应的元素编号,相应的配分函数定义为

式中,q为配分函数的阶数,取值范围为不等于零的整数.

当配分函数满足幂律关系,Z(a,q)～aτ(q)表明时间序列有标度不变性,τ(q)为幂指数,如果τ(q)是一条直线,时间序列是单分形;否则,就是多分形.多分形性质可用分形维数D(h),即多重分形谱来表示,可以由勒让德变换得到

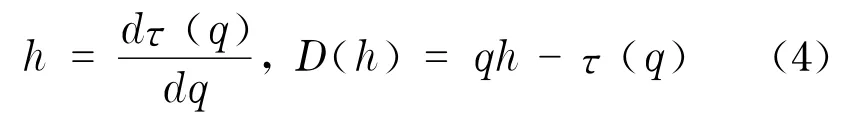
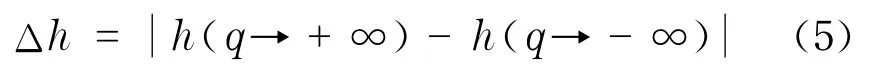
由于勒让德变换在计算中涉及到求导数,这在实际计算中会导致不可接受的误差,因此,往往先对离散的τ(q)进行拟合,再进行式(4)的变换

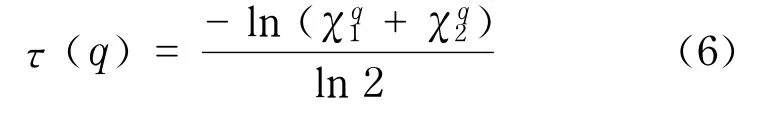
式中,χ1和χ2为统计参数,决定分形谱的特征.

2 模 型

2.1 混合分数布朗运动(FBM)

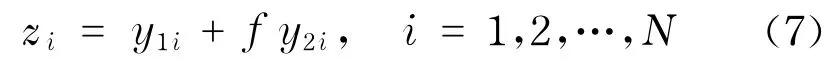
式中,参数f为调节序列中两个指数序列成分相对强度的参数,取值范围0≤f≤1.

序列z就是序列y1和序列y2叠加后的混合序列.

2.2 二进制多分形模型(BMF)

构建长度为N的时间序列

式中,参数w的取值范围为0＜w＜0.5;φ(k)为转换函数,其作用是将任意十进制数k转换成其相应二进制数,然后数其中数值位是1的个数,例如,φ(13)=3,因为,13的二进制表示为1101,其共有3个1.

文献[19]证明了该序列具有多分形性质,并给出了多分形谱的解析结果.该时间序列具有长程相关性.

2.3 数值分布引起的多分形模型(DMF)

多分形序列通过随机方式产生,即序列值的生成服从某一概率密度函数,此类序列没有长程关联特性[19].

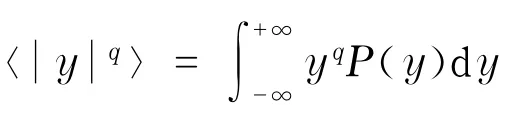
3 结 果

作为一个典型的实例,图2给出了休斯特指数为0.3和0.7的两个分数布朗运动混合序列的度分布,其中,混合相对强度f为1.p(k)表示序列可见图的度分布,一般情况下,无标度网络对应的度分布服从幂率分布,即p(k)～k-α,幂指数α被称为无标度指数.由p(k)图可以发现原始序列和混合序列的可见图均为无标度网络,并且混合序列的无标度指数与H=0.3(休斯特值较小)的原始成分序列的无标度指数相近.再通过对混合序列的小波分析,发现混合序列具有多分形特征,在多重分形谱D(h)图中,可以明显看到所分析的混合序列具有分形强度Δh=0.33,即表明该序列为多重分形序列.同时,从质量指数τ(q)拟合图中H=0.31进一步印证了在多成分序列的竞争问题中,采用不同的休斯特指数和混合强度进行的大量的计算表明,分数布朗运动的混合序列具有多分形性质,同时,对应的可见图具有无尺度特征,并且度分布的斜率由休斯特指数小的成分决定.

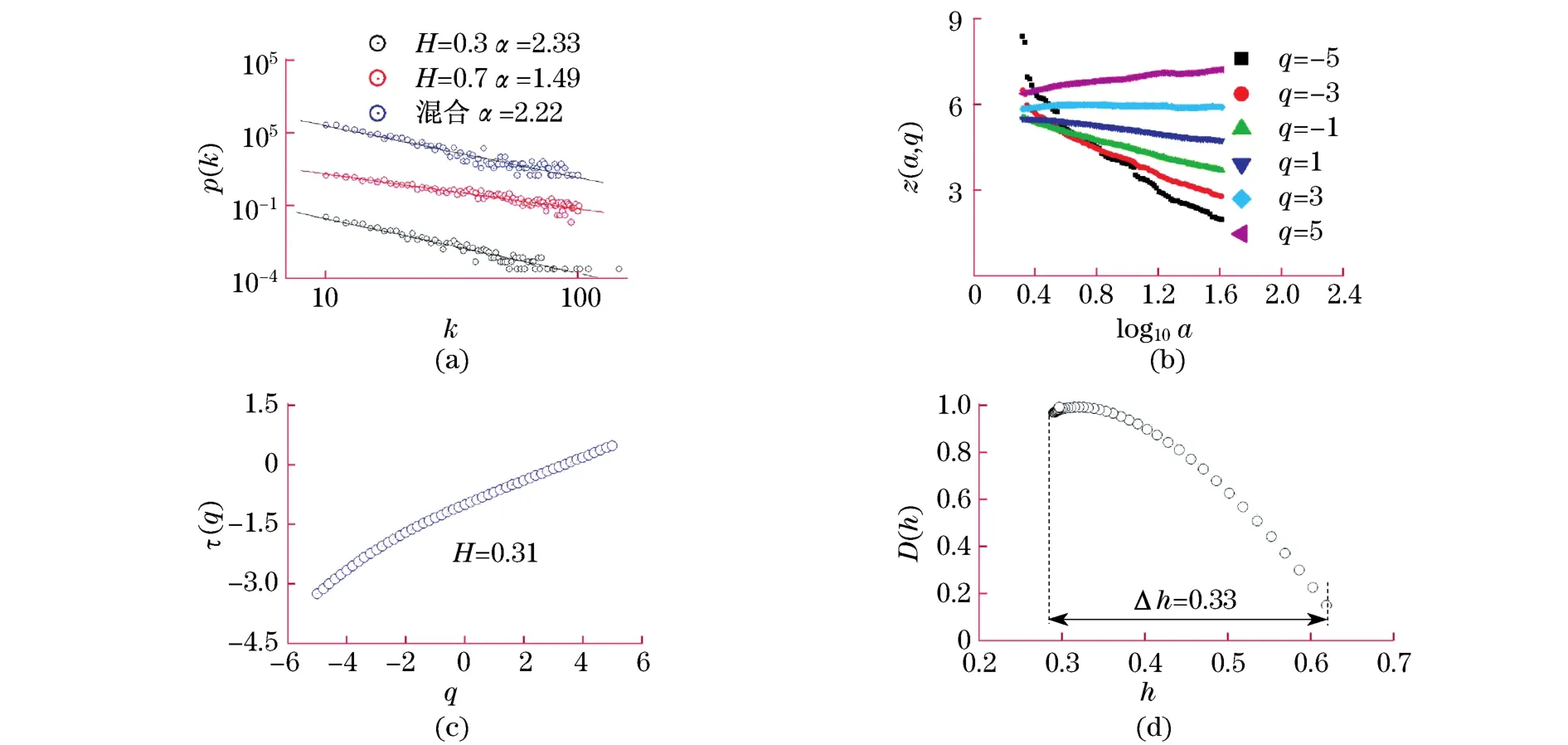
图2 混合分数布朗运动多分形和无尺度性质Fig.2 Multi-fractal and scale-free characteristics for mixture series of fractal Brownian motions

二进制多分形模型序列,为了得到其全部的可见图性质,调节参数w以0.05为间隔,从0.55～0.95,所有可见图的度分布结果如图3所示.

图3给出了BMF模型产生的时间序列的可见图的度分布,可以明显看到这些度分布不具有无尺度特征,只有在w接近于0.5,也就是时间序列接近于单分形的时候,度分布逐步过渡到近似的幂律分布. 图4给出了DMF模型产生的时间序列可见图的度分布.一般来讲,这些度分布也不具有无尺度特征,只有在β较大,度分布才过渡到幂律分布.当β较大时,概率密度函数具有渐进形式P(y)～y-3,对于这一分布指数为3的概率分布,在很大程度上与泊松分布是难以区分的,因此,这种模型产生的多分形时间序列的可见图不具有无尺度特征.

图3 二项式模型产生多分形的可见图度分布Fig.3 Degree distributions for visibility graphs of BMF model generated series

图4 数值分布多分形模型产生序列可见图的度分布Fig.4 Degree distributions for visibility graphs of DMF model generated series

4 结 论

鉴于实际问题中普遍存在的时间序列具有多分形特征,本文考察了不同的形成机制导致的多分形序列的可见图的拓扑结构属性,发现分数布朗运动的叠加导致的时间序列具有多分形特征,对应的可见图具有无标度特征,并且分形行为由休斯特指数小的成分决定,而二进制多分形和数值分布多分形模型产生的时间序列没有无标度特征.综上,可以得出的结论是传统的小波分析提取多分形特征的方法并不能分辨不同产生机制得到的多分形,而单独使用可见图方法也不能分辨单分形与多个单分形叠加导致的混合序列,必须联合运用这两种方法才能提取到关于序列形成机制的更多的信息.

[1] ZHANG J,SMALL M.Complex network from pseudoperiodic time series:Topology versus dynamics[J].Phys Rev Lett,2006,96:238701.

[2] ZHANG J,LUO X,NAKAMURA T,et al.Detecting temporal and spatial correlations in pseudo-periodic time series[J].Phys Rev E,2007,75:016218.

[3] XU X,ZHANG J,SMALL M.Super-family phenomena and motif of networks induced from time series[J].Proc Natl Acad Sci,2008,105:19601-19605.

[4] YANG Y,YANGH.Complex network-based time series analysis[J].Physica A,2008,387:1381-1386.

[5] WANGJ,YANG H.Complex network-based analysis of air temperature data in China[J].Mod Phys Lett B,2009,23:1781-1789.

[6] DONNER R V,ZOU Y.Recurrence networks-a novel paradigm for nonlinear time series analysis[J].New J Phys,2010,12:033025.

[7] GAOZ,JIN N.Flow-pattern identification and nonlinear dynamics of gas-liquid two-phase flow in complex networks[J].Phys Rev E,2009,79:066303.

[8] GAO Z,JIN N.Community structure detection in complex networks with applications to gas-liquid twophase flow[J].LNICST,2009,5:1917-1928.

[9] LUO F.Constructing gene co-expression networks and predicting functions of unknown genes by random matrix theory[J].BMC Bioinformatics,2007,8:299.

[10] LACASA L,LUQUE B,LUQUE J,et al.From time series to complex networks:The visibility graph[J].Proc Natl Acad Sci,2008,105:4972-4975.

[11] LACASA L,LUQUE B,LUQUE J,et al.The visibility graph:A new method for estimating the Hurst exponent of fractional Brownian motion[J].Europhys Lett,2009,86:30001.

[12] YANG Y,WANGJ,YANG H,et al.Visibility graph approach to exchange rate series[J].Physica A,2009,388:4431-4437.

[13] SHAO Z.Network analysis of human heartbeat dynamics[J].Appl Phys Lett,2010,96:073703.

[14] ZHAO D,LI X.Comment on“Network analysis of human heartbeat dynamics”[J].Appl Phys Lett,2010,96:266101.

[15] NI X,JIANG Z,ZHOU W.Degree distributions of the visibility graphs mapped from fractional Brownian motions and multi-fractal random walks[J].Phys Lett A,2009,373:3822-3826.

[16] YANG H,YIN C,ZHU G,LI B.Self-affinefractals embedded in spectra of complex networks[J].Phys Rev E,2008,77:045101.

[17] 王建波.基于复杂网络理论的时间序列分析[D].上海:上海理工大学,2010.

[18] 赵丽丽,唐镇,王建勇,等.基于复杂网络理论的时间序列分析[J].上海理工大学学报,2011,33(1):38-44.

[19] KANTELHARDT J W.Multifractal detrended fluctuation analysis of nonstationary time series[J].Physica A,2002,316:87-114.

Visibility graph approach for multi-fractal series analysis

TANGZhen1, WANGJian-yong2, YANGHui-jie1
(1.Business School,University of Shanghai for Science and Technology,Shanghai 200093,China;2.Department of Physics,Xingtai College,Xingtai 054001,China)

Visibility graph method is used to map multi-fractal series to complex networks.Intrinsic traits of multi-fractal series generated by different dynamical mechanisms were compared.It is found that mixture series constructed by superposition of several mono-fractal Brownian motions behave generally with multi-fractal character and the corresponding networks are scale-free.While for the multi-fractal series generated by theoretical models,the corresponding visibility graphs display complicated behaviors rather than scale-free.In order to distinguish between these different generators,joint use of wavelet analysis and visibility graph is required to make clear the dynamical mechanisms embedded in multi-fractal time series.Visibility graph method is a necessary complement to traditional time series analysis approaches,which has potential use in detecting dynamical mechanisms of complex systems from output series.

visibility graph;multi-fractal time series;degree distribution

N 941

A

1007-6735(2011)04-0357-05

2011-04-08

国家自然科学基金资助项目(10975099,10635040);上海市重点学科建设资助项目(S30501);上海市高等学校特聘教授(东方学者)岗位计划资助项目

唐 镇(1984-),男,硕士研究生.研究方向:非线性时间序列.E-mail:ad_min09@126.com杨会杰(联系人),男,教授.研究方向:复杂系统理论与系统生物学.E-mail:hjyang@ustc.edu.cn