应急系统中逃生与疏散策略的研究

高 岩, 刘 磊, 杨建芳

(上海理工大学管理学院,上海 200093)

应急系统中逃生与疏散策略的研究

高 岩, 刘 磊, 杨建芳

(上海理工大学管理学院,上海 200093)

介绍了应急机构选址和人员车辆等逃生与疏散策略,分析了目前该领域的研究进展.考虑到逃生/疏散问题存在很多不确定因素,通常需要在冲突环境下做出决策,所以在很大程度上它涉及到多种因素的相互作用.文中对有多个安全出口的逃生/疏散问题提出了一种微分对策方法,将逃生个体作为一个动态系统,看成微分对策局中人的一方,同时将不确定因素看作局中人另一方.通过构造捕获区和逃逸区的Hamilton函数得到二目标微分对策的解.

应急系统;突发事件;复杂系统;疏散;逃生

近年来灾害频发,应急系统管理逐渐引起人们重视,其研究也不断地深入.应急技术层面的研究是应急系统管理的重要组成部分,发挥的作用日益显著.应急系统是一个复杂开放系统,对应的策略称为应急系统管理.应急系统管理是冷战末期产生的术语,它由民防(civil defense)衍生而来,美国在第一次世界大战中建立了民防制度,用以避免美国公民受战争的打击.1979年,卡特政府成立了联邦应急管理署(FEMA),这是应急系统管理发展史上具有重要意义的大事.

我国是世界上少数灾害种类最多的国家之一,地震、洪涝及台风等自然灾害和火灾、交通事故、化学事故等频繁发生.2003年在中国的SARS肆虐传播,使得应急管理的理念在我国开始得到各级政府和广大学者的重视,其价值在于让人们认识到对待灾难的应对手段是认识灾难并及时给出防止灾难的科学技术方法[1].近几年突发事件更是频发出现,例如,2008年的汶川大地震,2009-2010年出现的西南地区干旱、西北雪灾、全国大范围的洪灾、以及2010年上海发生的“11.15”特别重大火灾事故等,使得应急管理的作用在社会上日显突出,各级政府投入了人力和财力开展这方面的研究工作.我国在应急管理领域的研究主要集中在自然灾害、人为灾害和工程系统灾害方面的应用研究,尽管众多专家学者基于不同的实际背景采用不同方法进行这方面的研究,并取得了大量的研究成果,但还缺乏基础的、普适的理论成果.

应急系统管理研究主要分3方面:应急系统的政策和制度设计;应急机构选址及应急物资调度;突发事件中的人员、车辆等逃生与疏散策略.第一项属政策层面的研究工作,第二项和第三项属技术层面上的研究工作,本文将讨论应急系统管理中技术层面上的问题,特别是逃生与疏散策略的方法研究.

1 应急机构选址

应急机构选址及应急物资调度是处理应急系统的重要研究工作.它要求突发事件发生后,人们对应急机构(包括物资供应点、医疗机构、救助机构等)位置设定和应急物资供应方案做出快速决定.这方面的工作主要集中在相应问题定量模型的建立和快速优化算法的设计上,有关这一研究领域国内外学者开展了大量研究工作.何建敏等[2]比较系统地给出了应急机构选址和资源调度等问题的基本模型和算法.韩强[3]利用双层规划将多出救点多应急点之间的单资源物资调度问题转化为带限制的运输问题来处理.国际上,Beraldi等[4]给出了应急车辆定位的一个统计模型,根据其不确定性的特点采用随机处理方式,给出了启发式方法.Sheu[5]基于发生大规模自然灾害时信息不完全的特点下,提出了一种动态的救灾应急物流需求管理模式.Hu[6]针对有多种运输方式情况下,采用免疫算法考虑如何尽快将应急物资及时有效地发送到应急点.文献[7]从对应急物资的准备上进行了研究,解决了如何合理安置库存点以及如何确定每个库存点的库存量,从而保证一旦出现突发事件,能及时有效地保证物资供给.

2 疏散与逃生策略

随着城市化进程的加速,大城市的建筑密集程度和人口密度迅速增加,空间日渐狭小,而流动人口不断增加,使得人员应急疏散问题更加突出.一旦出现突发事件,往往会导致人群、车辆拥挤的现象,结果造成大量的人员伤亡和财产损失.应急疏散是减少生命财产损失,特别是减少群死群伤事故发生的有效手段.因此,对密集人群和车辆等的管理、受困群众的疏散是应急管理中的一个重要环节.

应急疏散理论的研究分微观和宏观两种.在宏观模型中假设每个个体行为相似,从群组的角度进行研究;另一个是微观模型,它主要是通过模拟待疏散人员的行为来进行分析.宏观模型的构造相对简单,是早期多采用的疏散模拟模型,主要包括排队模型、路径选择模型及随机模型等.微观模型采用气体或液体的流动来模拟行人的运动行为,并考虑行人意图、期望速度和个体之间的相互作用.微观模型主要包括基于元胞自动机的疏散仿真模型、基于物理作用的社会力模型及基于多智能体系的疏散仿真模型等[8].

Hamacher等[9]对疏散问题的宏观模型进行综述,所列出的模型主要应用于建筑物火灾事故的疏散,也可以用于区域疏散,将时间作为主要考虑因素,给出了多个基于动态网络流的数学模型.Ren等[10]仿照基于数值模拟的火灾,使条件类似于现实生活,利用一个多网格、多基态数据库模型模拟来克服传统传播模拟烟雾的缺点,仿真火灾中的紧急疏散.张江华等[11]利用图论中网络优化思想的启发式算法考虑存在优先顺序的多源点和容量限制情形下的应急疏散.Zheng等[12]考虑每条路径上疏散人员的数量具有随机性、不确定性,基于高斯贝叶斯网络预测模型,结合人流特点、最优疏散路径以及疏散决策,利用最小疏散时间获得路径选择的概率来验证高斯贝叶斯网络预测模型回归系数.Ng等[13]在疏散人员(看成需求)和疏散路径容量(看成供给)不确定性的基础上建立疏散路径规划模型,确定需求通货膨胀量和供应通货紧缩量来保证可靠性水平.Xie等[14]利用集成拉格朗日松弛和禁忌搜索方法讨论了巷的疏散网络优化问题.

疏散问题具有高度动态性和不确定性,从有效的实时应急疏散角度,一些学者进行了有效研究.Hamza-Lup等[15]借助于电子技术,通过网络传感器的可利用数据获得实时交通信息,采用动态生成疏散计划来进一步改善智能交通疏散管理系统.Chen等[16]考虑了大型室内场所(如商场、地铁站)的实时应急疏散,利用快速流的控制算法来计算疏散路径和撤离总人数,确定最小的总疏散时间和每条路径上的最优疏散人数.现有的这些实时模型主要是基于动态网络技术,然而该技术往往不能充分反映应急疏散问题高度的动态性和不确定性.Liu等[17]针对实时交通管理的应急疏散,结合动态网络技术和自适应控制方法,提出了一种参考自适应控制的模型(MRAC),其主要思想是将待疏散的交通网络看成一个动态系统,该系统的状态可以通过现有的应急部署传感装置获得,它是在常规的动态交通分配模型(DTA)中采用自适应控制,通过传感系统获得所需要的状态和当前交通通行状态.而传感系统是可评估的,并且可以反馈到自适应控制模型产生实时交通控制方案.由于这种自适应控制模型的预测是短时间的并且基于最新的交通状况,因此,可以大大减少常规DTA模型的预测错误.该模型与传统的疏散模型不同之处在于不只是考虑交通分配的描述或者对某种应急方案的模拟仿真,而是从常规短期预测模型、描述性现实世界模型和反馈控制系统的设计3个方面去研究应急疏散.同时需要指出的是,该模型考虑的是在简化模式下假设完美的严格控制,但在现实中软控制装置得到广泛的应用;另外,模型中假设在整个疏散过程中始点和终点间动态需求矩阵是给定的固定值,实际上需求矩阵是随着时间变化而变化的;文中也没有考虑资源分配问题.作者所提出的模式可以适用任何情况的疏散,但是,不同类型的疏散有其自身的特征,因此,根据不同疏散情况需要作进一步改进.

3 逃生与疏散策略的微分对策方法

在人员和车辆等疏散过程中,人们关心的是整体能够逃离危险区,到达安全地带,然而这是以每个个体均能实现有效逃离为前提的.本文讨论个体处于整体环境状态下的逃生策略.考虑有多个安全点(室内场所通常为安全出口等),个体达到安全点的过程中有多种障碍,其中,一种为事先固定的障碍,通常为建筑物、山川及河流等,是确定的;另一种为不确定的障碍,通常包含其他个体或一些实时不确定因素.

本文试图采用微分对策方法来研究逃生/疏散问题.逃生/疏散个体作为一个动态系统,看成微分对策局中人的一方,来判断自己在有障碍物前提下是否可到达安全地点,同时将不确定因素看作局中人另一方.逃生个体通过微分对策方法来判断哪个安全地带是可达到的,从而选择自己的逃生路线.

微分对策(也称为动态博弈)是由于制导系统、航空航天技术等军事和民用技术发展的需要,于20世纪50年代发展起来的一个研究领域.1965年Issacs的专著《微分对策》的出版,标志着微分对策理论的建立.目前,微分对策已广泛应用于军事、航天航空、环境保护、经济管理及市场竞争等方面,成为控制科学中的一个重要研究领域.尤其在复杂系统管理方面,微分对策近年来已成为有关研究人员广泛应用的一个有效工具.

考虑二目标追扑逃逸微分对策

式中,x∈R n,x为状态变量;t≥0,t为时间,u∈U,u为局中人1的控制变量;v∈V,v为局中人2的控制变量;f为适当维数的Lipschitz连续函数.

设O,E⊂R n,局中人1的目标为在有限时间内达到O且避免E,局中人2的目标为永远避免O,或达到E,这就是二目标追捕逃逸微分对策.

这里所说的二目标微分对策不是二目标最优值函数,其中,目标E是一个状态约束,但本质上是仅对局中人1的一个约束,对局中人2不进行约束.

设D1⊂R n,如果对任意初始点x0∈D1和控制v(t)∈V,存在策略α:v(t)→u(t)使得局中人1在控制u(t)下状态x(t),在有限时间内达到O且避免E,则区域D1称为微分对策式(1)的捕获域.

设D2⊂R n,如果对任意初始点x0∈D2,和控制u(t)∈U,存在策略β:u(t)→v(t)使得局中人2在控制v(t)下x(t)永远避免O或在有限时间内达到E,则区域D2称为微分对策式(1)的逃逸域.

引入Hamilton函数

如果条件H1(x,p)=H2(x,p)成立,记H(x,p)=H1(x,p)=H2(x,p),则微分对策式(1)的捕获域和逃逸域可通过Hamilton函数H(x,p)以及集合边界点的切锥来表示[18],集合S⊂R n在点x∈S的切锥为

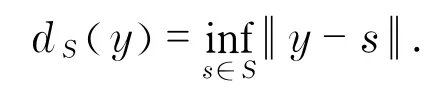
考虑逃生/疏散问题,记P1,…,P m为逃生/疏散个体,Q1,…,Q n为安全地带(出口),每个个体P i都希望尽快达到安全地带(出口)Q1,…,Q n中的一个.记个体P i达到出口Qj的时间为t ij,i=1,2,…,m,j=1,2,…,n,如果P i达不到出口Qj,则令t ij=∞.显然,t ij由状态方程(1)来确定.逃生/疏散问题是求解优化问题

即追求总体逃生/疏散时间最短.

个体P i的逃生/疏散策略如下:利用状态方程(1)判断事件发生时刻所在位置属于哪一个达目标Qj的捕获域,如果属于以Qj0为目标的目标捕获域,则说明P i可以向安全地带Qj0逃离.

考虑逃生/疏散个体Pi的动态演化为连续情形,即

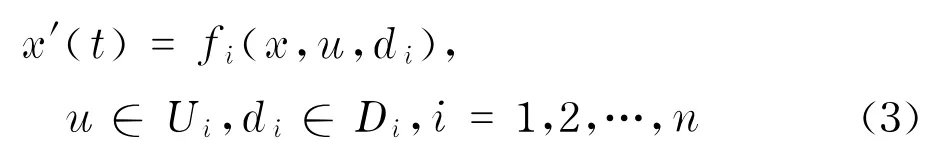
式中,x i为个体P i的状态变量;t≥0,t为时间;u∈U i,u i为个体P i的控制变量;d i∈D i,d i为逃生/疏散个体Pi所受的干扰因素;f i为适当维数的Lipschitz连续函数,i=1,2,…,n.

将关于微分对策式(1)的讨论应用于系统(3),即可确定逃生/疏散策略.

另外一种情况是在逃生/疏散个体Pi动态演化中扰动是离散状态,即在式(3)中每个扰动集合D i为有限点集,不妨记Di={d i1,…,d is},这就涉及到控制问题

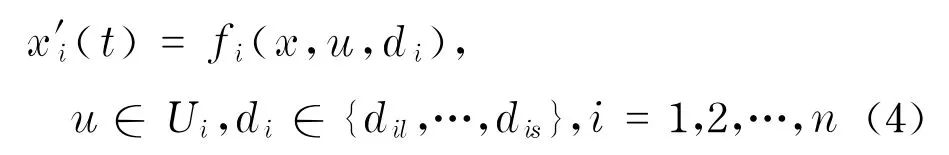
处理对策问题(4)有两种途径:一种方法是借助于连续微分对策进行保守估计;另一种方法是将其转化为微分包含.

考虑微分对策问题

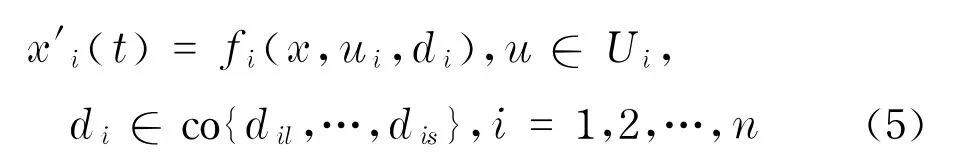
式中,co代表集合的凸.

显然,式(5)是一个连续微分对策问题,前面讨论的方法可以应用.由于{d i1,…,d is}⊂co{d i1,…,d is},所以,微分对策式(5)表示的捕获域一定是对策式(4)的捕获域.

微分包含方法是将问题(5)转化为微分包含.容易看出对策问题(4)可以等价地转化为微分包含

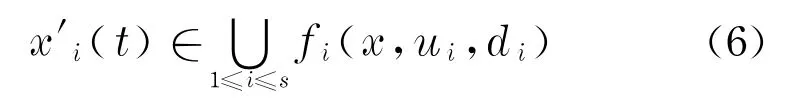
对微分包含式(6)进行控制即解决了微分对策式(4).有关微分包含的控制问题参见文献[19],本文不再详细讨论.

4 结 论

介绍了应急系统中的人群、车辆等逃生/疏散问题的技术方法.然后对有干扰因素的多个安全出口情形,个体对逃生/疏散安全出口选择策略进行了研究.考虑了两种动态模型,连续和离散情形,给出了微分对策研究框架,具体对策模型的控制方法、数值计算以及利用机器人进行仿真模拟试验是作者下一步的研究工作.

[1] 陈安,马建华,李季梅,等.现代应急管理应用与实践[M].北京:科学出版社,2010.

[2] 何建敏,刘春林,方磊,等.应急管理与应急系统---选址、调度与算法[M].北京:科学出版社,2005.

[3] 韩强.一类应急物资调度的双层规划模型及其算法[J].中国管理科学,2007,15(z1):716-719.

[4] BERALDI P,BRUNI M E.A probabilistic model applied to emergency service vehicle location[J].European Journal of Operational Research,2009,196(1):323-331.

[5] SHEN J B.Dynamic relief-demand management for emergency logistics operations under large-scale disasters[J].Transportation Research,Part E,2010,46(1):1-17.

[6] HU Z H.A container multimodal transportation scheduling approach based on immune affinity model for emergency relief[J].Expert Systems with Applications,2011,38(3):2632-2639.

[7] CAMPBELL A M,JONES P C.Prepositioning supplies in preparation for disasters[J].European Journal of Operational Research,2011,209(2):156-165.

[8] 陈安,陈宁,倪慧荟.现代应急管理理论与方法[M].北京:科学出版社,2009.

[9] HAMACHER H W,TJANDRA S A.Mathematical modeling of evacuation problems-A state of the art[C]//MICHAEL S,SOM DS.Pedestrian and Evacuation Dynamics.Berlin:Springer-Verlag,2002,227-266.

[10] REN A Z,CHEN C,LUO Y.Simulation of emergency evacuation in virtual reality[J].Tsinghua Science&Technology,2008,13(5):674-680.

[11] 张江华,刘治平,朱道立.多源点突发灾害事故应急疏散模型与算法[J].管理科学学报,2009,12(3):111-118.

[12] ZHENG X P,LIU M.Forecasting model for pedestrian distribution under emergency evacuation[J].Reliability Engineering and System Safety,2010,95(11):1186-1192.

[13] NG M W,WALLER S T.Reliable evacuation planning via demand inflation and supply deflation[J].Transportation Research,Part E,2010,46(6):1086-1094.

[14] XIEC,TURNQUIST M A.Lane-based evacuation network optimization:An integrated Lagrangian relaxation and tabu search approach[J].Transportation Research,Part C,2011,19(1):40-63.

[15] HAMZA-LUP G L,HUA K A,PENG R.Leveraging etransportation in real-time traffic evacuation management[J].Electronic Commerce Research and Applications,2007,6(4):413-424.

[16] CHEN P H,FENG F.A fast flow control algorithm for real-time emergency evacuation in large indoor areas[J].Fire Safety Journal,2009,44(5):732-740.

[17] LIU H X,BAN J X,MA W T,et al.Model reference adaptive control framework for real-time traffic management under emergency evacuation[J].Journal of Urban Planning and Development,2007,133(1):43-50.

[18] CARDALIAGUET P,QUINCAMPOIX M,SAINT-PIERRE P:Pursuit differential games with state constraints[J].SIAM Journal on Control and Optimization,2001,39(5):1615-1632.

[19] AUBIN J P,CELLINA A.Differential Inclusions,Set-Valued Maps and Viability Theory[M].Berlin:Springer-Verlag,1984.

Stragegy of emergency evacuation in emergency system

GAOYan, LIULei, YANGJian-fang(Business School,University of Shanghai for Science and Technology,Shanghai 200093,China)

The location of emergency systems and the emergency evacuation strategy were introduced and the recent advances of the study in this area were analysed.In fact,there are commonly many uncertain factors during the decision making process in emergency management.The outcome of emergency depends usually on the effects of two or more factors.A method of pursuit-evasion differential games with two targets was proposed to study the emergency evacuation with several security points.Escaping individual was regarded as a dynamic system and as one party of differential games while the uncertain factors as the other party.The solution of the differential game was obtained through constructing Hamilton functions.

emergency system;disaster and accident;complex system;evacuation;escape

N 945.15

A

1007-6735(2011)04-0321-05

2011-07-17

上海市科学技术委员会地方高校能力建设资助项目(10550500800);上海市重点学科建设资助项目(S30501)

高 岩(1962-),男,教授.研究方向:系统分析与优化.E-mail:gaoyan@usst.edu.cn