基于ANSYS的异步电动机电磁场分析

王水发，陈德为

(福州大学机械工程及自动化学院，福建 福州 350108)

1 引言

异步电动机作为一种典型的电能—机械能转换装置，具有结构简单、制造成本低等优点，已广泛应用于人们的日常生产生活中。但在电机的使用过程中，不可避免的出现了各种各样的故障，严重影响了人们的生产生活。因此，对电机的各种运行状况和故障进行分析，以便进行优化设计具有重要的实际意义。传统的电机电磁设计和故障分析都基于经典的电机电路计算方法，即“路”的思想［1］。虽然这种方法计算简单，但由于电机空间的复杂性，它不能考虑电机材料的磁饱和、定转子齿槽形状和集肤效应等因素给电机带来的影响。随着计算机技术的高速发展，使将有限元“场”的方法引入到电机的分析中成为可能，它能精确的分析出电机的运行情况，以便进行故障诊断和优化设计。而ANSYS软件是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件。其电磁模块和电路模块能很好的对电机的电路和电磁场进行分析，具有很强的实现耦合功能，并且具有强大的后处理功能，能够以图表、曲线等形式显示或输出，以供我们分析处理，还有提供了功能强大的APDL语言，利用它可以简单的实现某些GUI无法实现或实现起来很烦琐的功能，避免重复工作。本文采用了电机经典的“路”思想和有限元“场”的思想相结合的方法，即场路耦合法［2－5］，利用ANSYS软件对一台异步电动机进行谐波仿真分析和伪静止瞬态分析，分别用这两种方法分析出电动机在空载与堵转等运行状况下的二维电磁场。

2 电磁场分析的基本原理

电磁场理论是由一套麦克斯韦方程组描述的，它的分析和研究也是基于麦克斯韦方程组。麦克斯韦方程组实际上是由安培环路定律、法拉第电磁感应定律、高斯定律和高斯磁通定律四个定律组成的，其微分形式如下所示［6］:

上述方程组中:H为磁场强度矢量;B为磁通密度矢量;E为电场强度矢量;D为电位移矢量;J为传导电流密度矢量;ρ为自由电荷密度。

在电磁场问题中，以上四个方程存在以下的关系:

式中:ε为介电常数;μ为磁导率;σ为电导率。

3 电机场路模型的建立

3.1 电机等效电路模型的建立

本文采用的是场路耦合的方法，所以先把电机定子内的相绕组分为直线和端部两部分进行考虑(如图1所示)。端部用电阻和电感来等效代替，电阻表示端部本身的阻值，而电感用来模拟电机漏抗的影响。在进行谐波分析时，由于其只考虑基波的影响，故此时电感代表定子相绕组端部漏电感和谐波漏电感之和。而在进行伪静止瞬态分析时，因为其已经考虑了谐波的影响，故此时电感只代表端部的漏电感。直线部分是以电流和矢量磁位为变量，用有限元的方法进行迭代计算，实现场路耦合。其相绕组场路耦合等效电路如图2所示，因此电机定子相绕组电路的方程式为:

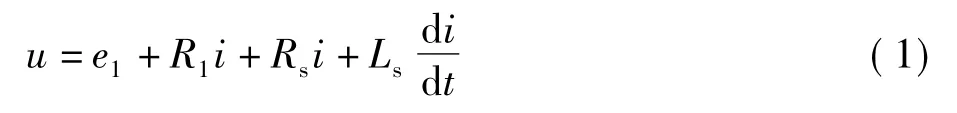
式中，u和i分别为电机定子相电压和相电流;e1和R1分别为电机定子相绕组直线部分的感应电动势和电阻;Rs定子相绕组端部电阻;谐波分析时，Ls为定子相绕组端部漏电感和谐波漏电感，伪静止瞬态分析时，Ls只为定子相绕组端部漏电感。

图1 电机定子相绕组的结构示意图

图2 电机定子相绕组的场路耦合等效电路

因为本文分析的异步电动机转子是鼠笼转子，其等效电路可按照其空间位置进行连接，转子导条、端环电阻和漏感组成的等效电路，满足基尔霍夫定律，其等效电路模型如图3所示。

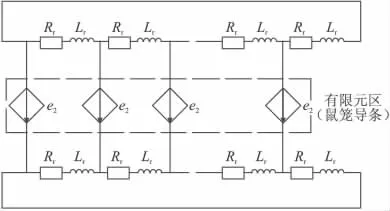
图3 鼠笼转子的场路耦合等效电路

3.2 电机二维场模型的建立

首先，在进行异步电动机二维有限元电磁场分析时，精度在工程允许的范围内，需先对模型的边界条件进行假设，以便简化计算。本文模型分析做假设如下:

(1)忽略电机端部电磁场的影响，即电机沿轴向的每个横截面的电磁场没有变化。

(2)电机定子以外的空间不存在漏磁场。

(3)电机各部件材料各向同性。

(4)忽略位移电流。

基于以上的假设，电机的二维电磁场求解区域满足涡流方程:

将电机的求解区域离散成很多网格单元，电机的网格划分和整体的场路耦合模型分别如图4、5所示。

因为电机定、转子的感应电动势e1、e2都是矢量磁位和定、转子电流的函数，再根据电机的场边界条件和路的边界条件，即定子外圆的=0和三相相位相差120°的交流电电压。以矢量磁位和电流为变量，离散求解区域，建立一个一组非线性方程组进行迭代求解，最后得出电机求解区域电磁场分布。

4 模型仿真与结果分析

本文仿真采用的是Y90L－4异步电动机，其基本参数如表1所示。

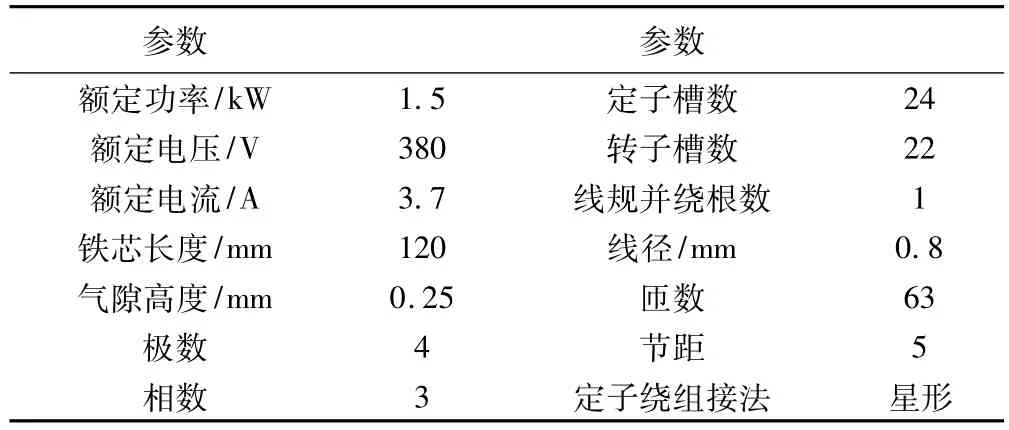
表1 Y90L-4异步电动机的基本参数

根据表1中的基本参数，在ANSYS软件中建立电机的二维物理模型，选用PLANE53单元［7］作为单元分析类型(可以通过设置单元的实常数来改变定子绕组电流的方向)，并分别将每槽定子绕组和转子导条所有节点的电流(CURR)和感应电动势(EMF)自由度都进行耦合;选用CIRCU124单元［7］作为电路仿真单元，在定子绕组和转子导条处，通过设定单元属性实现场路耦合。在上文假设的条件下，设定电机各部件的材料属性和模型的边界条件，以异步电动机定转子的整个圆面为求解区域，分别用两种方法进行分析，即谐波分析和伪静止瞬态分析。应用经典电机等效电路原理，在转子回路用串联的电阻代替负载的影响，即用s*σ子的电导率进行设置。通过改变转差率，可得电机多种负载情况下的磁场分布和定转子电流等。

4.1 谐波磁场分析

非线性时间—分析是基于能量等值方法用有效的B－H曲线代替实际的B－H曲线，将非线性的瞬态问题简化成非线性时间－谐波问题［8］。在给定正弦电源时，磁通密度B被假定为随时间成正弦变化的(在非线性瞬态分析中的磁通密度B是非正弦波形)，它只是真实磁通密度波形的时间基谐波近似值。图6为异步电动机在空载情况下的实部和虚部磁力线分布图;图7为异步电动机在堵转情况下的实部和虚部磁力线分布图;从图中可以看出，空载时，电动机的磁力线分布较好。在堵转状态下，转子导条顶部的磁力线分布非常密集，即存在严重的集肤效应。

图6 异步电动机在空载情况下的实、虚部磁力线分布

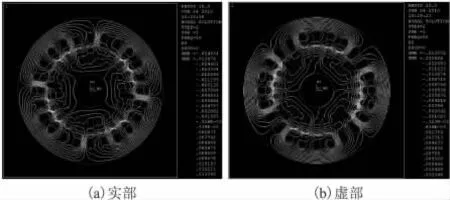
图7 异步电动机在堵转情况下的实、虚部磁力线分布

4.2 伪静止瞬态分析

伪静止瞬态分析与谐波相比，是使用了实际的BH磁化曲线［9］，并且在分析中考虑了场量的时间谐波的影响，能更精确的考虑磁饱和。其计算时间虽然比谐波分析更长，但与通用的时步有限元瞬态分析相比，已有较大的缩短。本文在进行伪静止瞬态分析时，将时间步长设置为0.001s，仿真时间设为0～0.12s。

图8是0.12s时电机在空载和堵转状态下的磁力线分布。图9分别是仿真过程中，电机在空载和堵转状态下的定子电流分布情况。从图中可以看出，定子三相电流经过一定的振荡后基本稳定成正弦波，但三相电流的幅值并非完全相同(谐波分析时，定子三相电流的幅值也非完全相同)，这是由于在进行谐波分析和伪静止瞬态分析中，都没有考虑转子旋转时齿槽效应的影响。

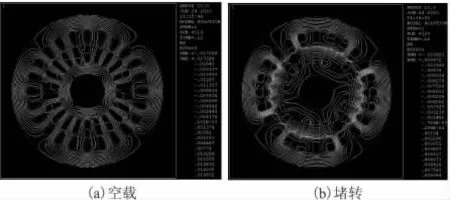
图8 0.12s时异步电动机空载和堵转情况下的磁力线分布

图9 异步电动机空载和堵转时定子电流的分布情况

表2为电动机在空载和堵载下，定子A相电流有效值的谐波分析值、伪静止瞬态分析值和实验值对比表。从表中可以看出，伪静止瞬态分析方法的分析误差相对较小，但两种分析方法都基本能满足工程精度要求。

表2 定子电流对比表

在电动机的电磁场分析中，要采用哪种分析方法进行分析，需根据实际需要进行取舍。一般情况下，若只关心电机计算参数的平均值和有效值，如不涉及其变化过程，可以选择谐波磁场分析。若更精确的考虑磁饱和，并且需要求出所需变量的变化过程，则可采用伪静止瞬态分析法，该模型所耗机时虽比谐波磁场分析多，但与考虑电机旋转时的时步有限元瞬态模型相比，所耗机时已少很多。

5 结论

本文建立了异步电动机的二维场路耦合有限元模型及其数学模型。分别利用谐波分析法和伪静止瞬态分析法两种方法对电动机进行电磁场分析，分别得到电动机在空载和堵转两种情况下的磁力线分布和定子电流。介绍两种方法各自的特点，并将分析结果与实验数据进行比较，精度满足工程要求，从而验证了所建电动机二维场路耦合有限元模型的正确性。通过此模型可以计算出与此电动机相关的很多特性参数，供电机的设计与分析使用，并为异步电动机的故障诊断和优化设计奠定基础。

［1］ 胡石，武建文，李德成，等.小型电动机现代实用设计技术［M］.北京：机械工业出版社，2008.3.

［2］ H.De Gersem et al.Field-circuit coupled models in electromagnetic simulation.Journal of Computational and Applied Mathematics［J］ .2004：125－133.

［3］ 孙宇光，王祥珩，桂林，等.场路耦合法计算同步发电机定子绕组内部故障的暂态过程［J］.中国电机工程学报，2004，1(24)：136 －141.

［4］ 夏正泽，刘慧娟.基于场路耦合法的异步牵引电机电磁场分析［J］.微电机，2009，3(24).

［5］ 范镇南，郭嘉.笼型异步电动机断相运行的场路耦合时步有限元计算分析［J］.微电机，2009，(6).

［6］ 汤蕴璆.电机内的电磁场［M］.北京科学出版社，1998.

［7］ ANSYS Inc.Theory Reference.

［8］ 阎照文，等.ANSYS10.0工程电磁分析技术与实例详解［M］.北京：中国水利水电出版社，2006.

［9］ 王爱龙，熊光煜.基于伪静止瞬态二维有限元模型的异步电机稳态计算［J］.电气应用，2006，3(25).