裂缝－孔隙油藏蒸汽辅助重力泄油过程的自适应网格数值计算

罗海山，王晓宏，施安峰

(中国科学技术大学热科学和能源工程系，安徽合肥230026)

裂缝－孔隙油藏蒸汽辅助重力泄油过程的自适应网格数值计算

罗海山，王晓宏，施安峰

(中国科学技术大学热科学和能源工程系，安徽合肥230026)

为提高裂缝－孔隙双重介质油藏蒸汽辅助重力泄油(SAGD)过程数值模拟的计算速度，根据温度、各相饱和度随空间变化的快慢在不同区域采用不同尺度网格，提出双孔双渗模型下的自适应网格算法及裂缝－基质方程的解耦方法。对给出的算例分别采用全精细网格及自适应网格算法进行计算。结果表明:自适应网格法处理这类带峰面非线性问题有很好的计算精度和计算速度;裂缝－孔隙双重介质油藏SAGD开采可能较早出现蒸汽窜顶这一不利于蒸汽能量利用率的现象。

蒸汽辅助重力驱油;稠油;渗流;多相流;自适应网格法;裂缝;双重介质

对于稠油油藏蒸汽辅助重力泄油(SAGD)热采过程，油藏中存在着一个不断膨胀的蒸汽腔，其界面附近相变非常剧烈，温度和各相饱和度梯度很大［1］，在变化剧烈的峰面附近，通常需要非常精细的网格，如果对全场都采用均匀精细网格，将需要很长的计算时间。为了提高计算速度，仅在需要的区域采用精细网格，而在其他区域采用较粗网格的自适应网格法得到了广泛的应用［2-4］，并逐步推广到多孔介质多相流及油藏数值模拟领域［5-9］。笔者对裂缝-孔隙双重介质稠油油藏SAGD过程的自适应网格计算方法进行研究，提出双孔双渗模型下的自适应网格算法及裂缝-基质方程解耦方法，以提高数值模拟的计算效率。

1 模型与控制方程

裂缝－孔隙双重介质由高渗透率低体积比的裂缝和低渗透率高体积比的基质岩石构成。在大尺度下，为使问题得到简化，通用的Warren-Root模型将双重介质描述成由正交的裂缝网络构成并将基质分割开来［10］。基质之间的流动通常很少，但基质与裂缝之间在压差作用下的流体交换(亦称窜流)通常是裂缝－孔隙双重介质油藏中石油被采出的主要原因。根据基质之间是否忽略流动和热传导，W-R模型又可分为双孔单渗模型［10-11］和双孔双渗模型［12］。由于双孔单渗模型忽略了基质岩石之间的热传导，考虑到岩石的热传导是SAGD开采的一个重要因素，因此本文中使用双孔双渗模型。

裂缝和基质的水组分质量守衡方程为

裂缝和基质的油组分质量守衡方程为

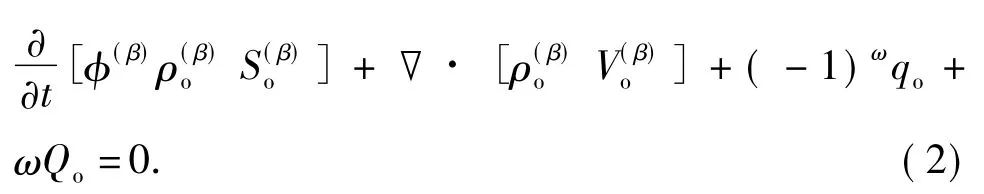
裂缝和基质的能量守衡方程:

其中

式中，f和m分别表示裂缝和基质;下角标w、g和o分别表示水、蒸汽和稠油;φ(β)为孔隙度;ρ、H、U分别为密度、焓和内能。

α相流体流动速度由达西定律确定为

式中，k和Krα分别为绝对和相对渗透率;对于稠油，黏度μα随温度变化非常快。

qα和E分别表示裂缝与基质之间的窜流量和热交换［10－14］，其表达式为

在热平衡方程(3)中，^Uα和^Hα取上游方向的值，即如果

相类似，方程(5)中“upstream”表示上游方向的值。σ是基质岩石的形状因子，可以根据基质岩石的特征长度L*估算为

根据Kazemi公式［15］，常数γ可简单取为12。井口源项Qα由经典的Peaceman公式［16］求得。

裂缝和基质中热传导系数为

油、水和气等各相压力之间的关系满足

其中

式中，pcow为油水毛管力;pcog为油气毛管力;S(β)l为液相总饱和度。

当水和蒸汽共存时，多孔介质内饱和蒸汽压力－温度关系［17］满足

其中，气体常数R=8.31 J/(K·mol)，水－汽毛管力

2 自适应网格法

自适应网格法包括网格结构、网格细化和粗化、网格细分准则以及自适应网格有限差分方程的求解步骤。

2.1 网格结构

自适应网格方法(AMR)是将整个流场的网格结构划分为若干层，层次由最粗层(k=1)到最细层(k=kmax)。相邻层的空间步长相差2倍或其他倍数(本文采用2倍)。对于均匀裂缝－孔隙双重介质的自适应网格法的流场计算，为使计算简便，将裂缝网格结构与基质网格结构绑定在一起，让它们的网格结构完全重合。

2.2 网格的细化与网格细分准则

为动态刻画峰面位置，须根据油藏物理量的变化情况判断是否需要重新划分网格结构，这就涉及到了网格的细化与网格细分准则。网格的细化是采用线性或高阶曲线插值以确定粗网格所覆盖的最精细网格上的物理量。本文讨论的SAGD过程问题，油藏中存在温度和各相饱和度峰面，则网格细分准则为对温度和各相饱和度设置一个阈值(εT和εSα)，如果任一粗网格内温度和各相饱和度的变化大于阈值，网格将予以细分。由于本文研究的介质含有裂缝和基质两个系统，因此设置的阈值同时包括裂缝与基质的温度和各相饱和度。

2.3 网格的粗化

新的网格结构确定后，需要确定新出现的粗网格上的物理量。对于新被激活的粗网格，由其覆盖的所有最精细网格上物理值求平均得到粗网格上的值(针对裂缝－孔隙油藏)。在本文中，孔隙度、压力和温度取算术平均，饱和度取加权算术平均(权值是孔隙度)，渗透率和热传导系数取调和平均。

2.4 自适应网格有限差分方程的求解步骤

自适应网格算法中，不同层次的时间步长是不同的。让不同层之间的Courant数νk=Δtk/Δxk相等，即时间步长与空间步长成正比［2］。这样，越粗的网格其时间步长越大，最粗层的时间步长是最细层时间步长的2n－1(n是总层数)倍。完整的一轮计算步骤从最细层到最粗层逐层推进，见图1。计算完最粗层后该轮计算结束。此后，须判断网格是否需要重新划分，在确定好网格结构后，进入下一轮计算，如此循环。

图1 自适应网格算法各层计算步骤Fig.1 Adaptive mesh refinement(AMR)calculation procedure for advancing solution on different level grids

3 方程的解耦

3.1 方程离散

在自适应网格算法中，只有被激活的网格参与计算，被激活网格的父网格或子网格不直接参与计算。计算是分层求解的，当计算某一层次时，假设当前的层次下被激活网格共有n个，使用有限体积法对方程组(1)～(3)进行全隐式离散，由于含有裂缝和基质两个系统，因此可分别得到两个3n阶的非线性离散方程组，其数学形式简化为

式中，F1对应裂缝方程组;F2对应基质方程组;Xf和Xm分别为裂缝方程组和基质方程组的待求主变量。

3.2 双孔双渗模型下裂缝－基质方程的解耦

对非线性方程组(13)和(14)使用牛顿迭代法，分别得到线性方程组

在双孔单渗模型下，由于忽略了相邻基质之间的相互影响，根据方程组(16)，任一被激活网格(用i标号)对应的基质方程组的主变量可用其对应的裂缝网格方程组的主变量表示为

将式(17)带入式(15)即可消去所有基质变量，从而只须求解一个3n阶的线性方程组。这样裂缝－基质方程组的解耦方法减少了一半的变量，大大减少了矩阵运算计算量［11］。然而对于双孔双渗模型，相邻基质网格之间存在着关联，为将双孔单渗模型下成立的方程组解耦方法推广到双孔双渗模型中，在牛顿迭代过程中让基质方程组(17)中的对流项与热传导项在迭代计算过程中都暂时“显式化”，即使用上一迭代步的值，从而实现裂缝－基质方程组的解耦。

4 算例

考虑一个长300 m、宽64 m、高32 m的裂缝－孔隙双重介质稠油油藏，长、宽、高方向分别用Z、X、Y表示。在油藏中间距离底部5 m的位置沿Z方向打一口300 m长的水平采油井，在采油井正上方5 m处平行打一口等长的注汽井。油藏两边取周期边界条件，上、下取无流边界条件(但不绝热)。油藏首先进行蒸汽吞吐，当注气井与生产井连通后开始进入SAGD过程。假设蒸汽在注气井内流动沿程没有损失，且油藏在Z方向上所有横截面没有区别，则该三维油藏模型可以简化为X、Y方向的二维油藏模型。油藏的参数如下:注蒸汽速度Qg(in)=100 t/d;注入蒸汽温度Tin=523 K;注入蒸汽干度95%;油藏初始温度T|t=0=320 K;油藏顶部初始压力产油井井底压力pwell=2 MPa;裂缝孔隙度φ0=0.01;基质孔隙度φ0=0.1;裂缝绝对渗透率10－13m2;基质绝对渗透率K(m)=1.97×10－15m2;裂缝初始各相饱和度|t=0=0;基质初始各相饱和度裂缝压缩系数10－8Pa－1;基质压缩系数稠油比热容cpo=2.0 kJ/(kg·℃);基质岩石比热容ρRcpR=2.39 MJ/(m3·℃)。

通常，裂缝的毛管力很小［14］，各相相对渗透率可近似等于各相饱和度［18］。本文中，裂缝内毛管力忽略不计。对于裂缝－孔隙双重介质流体的流动，基质内的毛管力却是一个很重要的角色［14］。这是由于基质毛管力通常比较大，会造成基质各相流体压力的较大不同。只要基质岩石是亲油的，基质就会在毛管力作用下吸入裂缝中的水并向裂缝排出油，这是裂缝－孔隙双重介质油藏中重要的驱油机制之一。使用经典的Brooks-Corey模型［19］计算基质内各相流体之间的毛管力和相对渗透率曲线，束缚水饱和度、束缚气饱和度、残余油饱和度分别取为0.2、0、0.2;启动油水毛管力、启动油气毛管力分别取20、50 kPa。由于是多相流，油相相对渗透率由Stone II模型［20］得到。

油藏模型方程离散所用的最精细网格边长为1 m，最精细网格对应的时间步长最高取0.5 d。自适应网格总层次取4，网格结构的划分准则使用裂缝和基质的温度和各相饱和度，阈值均取εT=5 K和εSα=0.05。采用预处理共轭梯度法求解代数方程组。图2为全精细网格与自适应网格法同一时刻的计算结果对比。

从图3可以看出，产油量在稳定上升，累积油汽比约为0.17。图2和图3的计算结果对比显示，采用全精细网格求解与自适应网格法求解的结果符合得很好。自适应网格结构随峰面位置而变。图4中给出第360 d时的自适应网格结构。

由图4可见，在远离峰面的位置都是粗网格，而在已经被峰面扫过的区域其细网格可以逐渐恢复成粗网格。

在同一台微机(CPU主频奔四1.6 GHz，内存2G)上，当程序计算到油藏SAGD开采的第360 d时，全精细网格的运算耗费时间为25 min，而自适应网格法仅用了3 min，自适应网格法的计算速度提高了7倍多。本文中只使用了64×32个网格数量即达到了8倍以上的计算速度，如果采用更多的网格数量或使用三维模型计算，则计算速度的提高将更加显著。

图2 第360 d时两种方法计算的油藏裂缝温度、压力、蒸汽饱和度和基质油饱和度等值线对比Fig.2 Comparison of numerical results between AMR solution and fine-grid solution at 360th day.

另外，从图3还可以看出，在第500 d附近存在一个拐点。在这之前累积油汽比在缓慢上升，但之后开始缓慢下降。累积油汽比的上升说明蒸汽能量的利用率可能出现了变化。对结果进行分析，发现第500 d前后正好是蒸汽腔开始触及油藏顶部的时刻，蒸汽腔的膨胀由rising方式变成spreading方式［21］，之后蒸汽腔与油藏顶部的接触面积逐渐扩大。图5显示了计算到第1 000 d时裂缝蒸汽饱和度的等值线。

图3 累积产油量和累积油汽比对比Fig.3 Comparison of cumulative oil production and cumulative oil-steam ratio

图4 第360 d的自适应网格结构Fig.4 AMR grid structure at 360th day

图5 第1000 d裂缝蒸汽饱和度等值线Fig.5 Fracture steam saturation contour line at 1000th day

从图5中可观察到，蒸汽腔已经窜顶，热量从顶部外泄到外界，形成热损失，而油藏侧向的膨胀程度不高，油藏许多位置还没被开采。这些现象对采油的经济效益将有负面影响。

5 结束语

裂缝－孔隙双重介质稠油油藏的SAGD开采是带峰面的强非线性问题。提出了双孔双渗模型解耦的方法。通过对算例的数值求解，将全精细网格与自适应网格法的计算结果进行了对比，显示出自适应网格法很好的计算速度和计算精度。在裂缝－孔隙双重介质油藏实施SAGD开采可能较早出现蒸汽窜顶这一不利于注入蒸汽的能量利用率现象。

［1］BUTLER R M，STEPHENS D J.The gravity drainage of steam heated to parallel horizontal wells［J］.JCPT，1981，90-96.

［2］BERGER M J，OLIGER J.Adaptive mesh refinement for hyperbolic partial differential equations［J］.J Comput Phys，1984，53:484-512.

［3］BERGER M J，COLELLA P.Local adaptive mesh refinement for shock hydrodynamics［J］.J Comput Phys，1989，82:64-84.

［4］VENUTURUMILLI R，CHEN L D.Numerical simulation using adaptive mesh refinement for laminar jet diffusion flames［J］.Numer Heat Transfer B，2004，46(2):101-120.

［5］TRANGENSTEIN J A.Multi-scale iterative techniques and adaptive mesh refinement for flow in porous media［J］.Adv in Water Resources，2002，25:1175-1213.

［6］NILSSON J，GERRITSEN M，YOUNIS R.Towards an adaptive，high-resolution simulator for steam injection processes［R］.SPE 93881，2005.

［7］韩大匡，陈钦雷，闫存章.油藏数值模拟基础［M］.北京:石油工业出版社，1993:254-259.

［8］谭未一，刘福平，李瑞忠，等.渗流方程的渗透率自适应权重网格粗化算法［J］.石油大学学报:自然科学版，2004，28(4):52-55.TAN Wei-yi，LIU Fu-ping，LI Rui-zhong，et al.Adaptive grid roughening algorithm for average permeability of fluid equations［J］.Journal of the University of Petroleum，China(Edition of Natural Science)，2004，28(4):52-55.

［9］WANG X H，QUINTARD M，DARCHE G.Adaptive mesh refinement for one dimensional three-phase flow with phase change in porous media［J］.Numer Heat Transfer B，2006，50:231-268.

［10］WARREN J E，ROOT P J.The behavior of naturally fractured reservoirs［J］.SPE J，1963，3:245-255.

［11］THOMAS L K，DIXON T N，PIERSON R G.Fractured reservoir simulation［J］.SPE J，1983，23:42-54.

［12］HILL A C，THOMAS G W.A new approach for simulating complex fractured reservoirs［C］.SPE Middle East Oil Tech Conference and Exhibition，Bahrain，11-14 March，c1985.

［13］PRUESS K，NARASIMHAN T N.A practical method for modelling fluid and heat flow in fractured porous media［J］.SPE J，1985，25(1):14-26.

［14］OBALLA V，COOMBE D A，BUCHANAN W L.Fac-tors affecting the thermal response of naturally fractured reservoirs［J］.The Journal of Canadian Petroleum Technology，1993，32(8):31-42.

［15］KAZEMI K，MERRILL L S JR，PORTERFIELD K P，et al.Simulation of water-oil flow in naturally fractured reservoirs［J］.SPE J，1976，16(6):317-326.

［16］PEACEMAN D W.Interpretation of well-block pressures in numerical reservoir simulation with nonsquare grid blocks and anisotropic permeability［R］.SPE 10528，1982.

［17］UDELL K S.Heat transfer in porous media heated from above with evaporation，condensation，and capillary effects［J］.Journal of Heat Transfer，1983，105:485-492.

［18］HONARPOUR，M M，KOEDERITZ F，HERBERT A.Relative permeability of petroleum reservoirs［M］.Boca Raton，FL:CRC Press Inc，1986:41.

［19］BROOKS R H，COREY A T.Properties of porous media affecting fluid flow［J］.Journal of Irrigation and Drainage Division，Proceedings of the American Society of Civil Engineers，1966，92(IR2):61-88.

［20］STONE H L.Estimation of three-phase relative permeability and residual oil data［J］.Journal of Petroleum Technology，1973，12(4):52-61.

［21］RENARD P，MARSILY G D.Calculating the equivalent permeability:a review［J］.Advances in Water Resources，1987，20:253-278.

［22］CHOW L，BUTLER R M.Numerical simulation of the steam-assisted gravity drainage process(SAGD)［J］.JCPT，1996，35:55-62.

(编辑 沈玉英)

Adaptive mesh refinement technique for numerical simulation of SAGD process in fracture-pore reservoirs

LUO Hai-shan，WANG Xiao-hong，SHI An-feng
(Department of Thermal Science and Energy Engineering，University of Science and Technology of China，Hefei 230026，China)

To improve the numerical simulation calculation speed for steam assisted gravity drainage(SAGD)process in fracture-pore dual-porosity reservoirs，the adaptive mesh refinement(AMR)algorithm as well as the fracture-matrix equation decomposition approach under a dual-porosity(DK)model was proposed by using different grid sizes in different regions based upon the spatial variations of the temperature and phase-saturations.The numerical results show that the proposed AMR technique dealing with such nonlinear problems with the front is fast and can give good precision compared with the fine-grid solution.It is also shown that the steam chamber could reach the top of the reservoir，which is harmful to the thermal efficiency of steam energy for the SAGD process in fracture-pore dual-porosity reservoirs.

steam-assisted gravity drainage;heavy oil;seepage;multiphase flow;adaptive mesh refinement;fracture;dual-porosity media

TE 345

A

10.3969/j.issn.1673-5005.2011.01.028

2010－06－22

中国科学院知识创新工程重大项目(KJCX1－YW－21);国家“863”计划项目(2006AA06Z228);国家自然科学基金项目(50674081)

罗海山(1982－)，男(汉族)，福建龙岩人，博士研究生，主要研究方向为多孔介质中流动理论和数值计算以及蒸汽热采稠油数值计算的自适应网格法。

1673-5005(2011)01-0140-06