基于DSA和FEM的电器绝缘结构自动优化设计
2011-09-26马爱清张周胜
马爱清,张周胜
(上海电力学院电力与自动化工程学院,上海 200090)
电器装置自动设计中,形状优化设计在改进电磁设备性能方面非常重要.根据寻优过程的不同,优化方法可以分为随机性优化和确定性优化两种.随机性优化方法包括基因算法、TABU算法和模拟退火法等,由于能给出全局优化解,在过去的十几年内,已被广泛应用于各种电磁工程设计[1-3].确定性优化方法,比如结合设计灵敏度分析的梯度法,尽管有时会陷入局部极小,但由于可以大幅度地降低寻优过程中目标函数的计算次数,最大限度地降低寻优过程中的计算代价,从提高计算量的角度,结合设计灵敏度分析的确定性方法更优于非确定性方法[4-6].本文将灵敏度分析(Design Sensitivity Analysis,DSA)、有 限 元 法(Finite Element Method,FEM)以及优化算法相结合,对2D电器装置的形状进行优化,给出了设计灵敏度分析公式及伴随变量方程的推导,并将该方法成功用于110 kV GIS光纤电流互感器的绝缘结构优化设计中.
1 结构优化模型
将结构模型、设计灵敏度分析和优化算法结合成为一个通用的系统,实现各种优化自动设计是非常必要的.图1所示的结构优化模型表示了形状优化设计问题的3个组成部分.

图1 结构优化模型示意
结构模型提供在静态或动态边界条件下结构的性能特性.结构参数是在构造目标函数及设计约束时用到的设计变量.在实际工程应用中,需要建立详细的有限元模型.优化模型将结构分析与优化算法相联系,目标函数值与性能约束值通过结构模型的有限元分析得到.而优化模型中所定义的目标函数最优解可通过优化算法求得.
2 2D静电场问题设计灵敏度分析
2D静电场的系统控制方程为:

式中:ε——介电常数;
φ——电势.
静电场的有限元分析可以最终归结为求解如下有限元方程:

式中:A——系统矩阵;
X——电位矩阵;
b——载荷向量矩阵.
静电场的形状优化设计都可以表示为:

式中:F——目标函数;
p——由表面节点组成的设计参数向量;
X——状态变量;
pmax,pmin——设计参数的上下限值.
关于设计变量的灵敏度可以推导如下:

对式(2)两边的设计变量p求导,并乘以伴随变量 λT[7,8],可以得到:

通过选择伴随变量,使得式(4)和式(5)中的dX/dp系数相等,因此可以得出伴随方程和灵敏度公式为:

式中的X就是式(2)的解.
根据最速下降法,利用已计算得到的灵敏度来更新设计变量:

式中:α——松弛因子.
3 有限元网格更新方法
形状优化设计的一个重要部分是随着设计变量的改变来更新有限元网格,并且应尽量使有限元网格均匀分布,它是保证计算结果精度的重要因素[9].
采用Delaunay三角剖分技术所形成的三角形网格,最小的内角是所有三角剖分中最大的,而且Delaunay三角剖分所形成的三角形最接近于等边三角形,因此该技术在实际应用中具有很大优势.其基本思想是:首先形成只有边界节点构成的开端网格,在此基础上,引进一个新节点,根据原判据修改原来的网格,以形成新网格;在新网格的基础上,再引进一个新节点形成新网格,依此循环直至引进全部节点.但节点的分布直接影响网格的优劣,在网格更新过程中,需要利用边界节点分布来有效控制内部节点的分布,以实现网格疏密连续过渡,避免出现太尖或太钝的三角形单元.
因此,可以采用基于Delaunay三角剖分的置换算法(Swapping Algorithm)[10].由于设计变量的改变,网格需要更新,如图2所示,边界单元较长的边上有可能产生新点P,而置换算法根据对角线的长度来修正P点的位置,尽可能地减少三角形网格的变形.
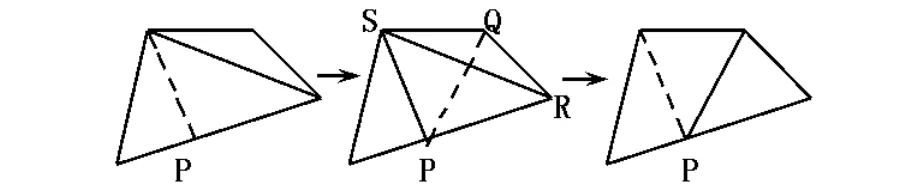
图2 网格更新中节点位置的修正
在设计变量改变后,需要对网格进行更新,在网格生成程序中采用Delaunay三角剖分算法和置换算法,所有的设计参数点可以被指定为单元边界的初始点,在每次优化迭代后,被改变的设计参数自动输入,作为边界的初始点,以产生新的网格.
4 优化算法流程
将有限元分析、最速下降法和网格更新方法相结合,形成新的2D形状优化设计算法,见图3.

图3 优化算法流程
显然,该优化设计算法仅需要进行有限元网格一次剖分,就可以大大缩短计算周期,节约优化设计的计算量.
5 GIS光纤CT绝缘结构自动设计
在电磁装置的自动设计中,灵敏度分析及有限元技术已得到广泛的应用[11,12].图4为110 kV GIS光纤CT绝缘结构中的一相高压电极简化模型.设计中,B可以在30~60 mm之间调整,R可以在10~25 mm之间调整.

图4 110 kV光纤CT绝缘结构示意
在绝缘结构设计中,静电场绝缘外表面期望的最大电场强度值可以由设计人员提出.
该设计中,目标函数定义为:

式中:E——绝缘外表面电场强度的最大值;
E0——所期望的电场强度设定值,当在高压电极和低压电极施加275 kV的电压时,希望得到 E0=9.0 kV/mm的设计值.
利用本文提到的灵敏度设计方法自动设计,通过5次迭代,当B=45 mm,R=20 mm时,得到了所期望的电场强度设计值E0=9.0 kV/mm.
为了检验设计的正确性,又通过有限元法求解该静电场,解得的结果为9.07 kV/mm.该结果与本文利用优化设计方法所得结果相比,二者的相对误差为0.7%,表明上述自动设计程序是有效的.
6 结语
在有限元方法的基础上,本文给出了2D静电场灵敏度分析设计的公式推导,以及整个优化算法的流程框图,通过计算目标函数对几何变量的灵敏度,来优化设计电器装置的绝缘结构.通过实例表明,本文所用方法在快速优化计算的同时,还可以保证计算结果的精度.
[1]汪友华,陈敏,刘福贵,等.改进的遗传算法及其在SF6灭弧室永磁场优化中的应用[J].中国电机工程学报,2001,21(10):43-46.
[2]杨仕友,倪光正,钱金根.电机电磁场的逆问题数值计算的改进TABU算法[J].中国电机工程学报,1998,18(2):83-86.
[3]杨仕友,倪光正.模拟退火算法的改进及其在电机电磁场逆问题数值计算中的应用[J].电工技术学报,1998,13(2):21-23.
[4]WANG S,KANG J.Shape optimization of BLDC motor using 3D finite element method[J].IEEE Trans.on Magnetics,2000,36(4):1 119-1 123.
[5]BYUN Jin-kyu,LEE Ju-hyun,PARK Il-han,et al.Inverse problem application of topology optimization method with mutual energy concept and design sensitivity[J].IEEE Trans.on Magnetics,2000,36(4):1 144-1 147.
[6]OKAMOTO Y,AKIYAMA K,TAKAHASHI.3D topology optimization ofsingle-pole-type head by using design sensitivity analysis[J].IEEE Trans.on Magnetics,2006,42(4):1 087-1 090.
[7]IOAN D,MUNTEANU I,CIUPRINA G.Adjoint field technique applied in optimal design of a nonlinear inductor[J].IEEE Trans.on Magnetics,1998,34(5):2 849-2 852.
[8]GITOSUSASTRO S,COULOMB J C,SABONNADIERE J C.Performance derivative calculations and optimization process[J].IEEE Trans.on Magnetics,1989,25(4):2 834-2 839.
[9]盛剑霓.工程电磁场数值分析[M].西安:西安交通大学出版社,1991:65-95.
[10]LAWSON C L.Software for C1interpolation in mathematical software III[M].New York:Academic press,1977:35-42.
[11]RAMIREZ J A,FREEMAN E M.Sensitivity analysis for the automatic shape design of electromagnetic devices in 3D using FEM [J].IEEE Trans.on Magnetics,1997,33(2):1 856-1 859.
[12]CUI Xiang,ZHANG Guo-qiang.Sensitivity analysis and automatic design of voltage ratio in an optical instrument voltage transformer[J].IEEE Trans.on Magnetics,1999,35(3):1 769-1 772.
