基于遗传算法与约束矩阵的工艺路线优化方法研究

王 军 孟庆智

(燕山大学机械工程学院，河北秦皇岛066004)

工艺路线的优化是CAPP(计算机辅助工艺过程设计)系统的关键技术与难点之一，是衡量CAPP系统智能化和实用化的一个重要标志，它在很大程度上决定了CAPP系统的应用水平［1］。其主要任务是按照工艺约束规则和一定的优化目标，对工件所有加工特征的加工方法进行排序，将得到的最优加工序列作为工件的工艺路线［2－3］。

工艺路线优化问题与其他优化问题不同，它求解的不是值优化而是排序优化，而且排序过程与机床、刀具、夹具、约束之间存在各种可能的联系，这使得工艺路线排序成为一个极其复杂的组合优化问题，其优化目标和约束条件都难以用明确的解析式表达，因此工艺路线的决策和优化问题很难用传统的优化算法来解决［4－5］。本文采用遗传算法进行工艺路线的优化决策。它以优化变量的某种形式的遗传编码为运算对象，以基因交叉重组和变异为基础进行全局搜索，不仅并行性高、鲁棒性强，而且个体的适应度评价也可以不依赖于目标函数的恰好估值。

本文在对工艺路线优化问题进行分析的基础上，建立工艺决策的数学模型，并利用约束矩阵来描述工艺约束关系，而且约束矩阵由系统自动生成，设计了用于保证加工元序列的满足约束关系的算法，对基于遗传算法的工艺路线优化决策方法进行了研究。

1 工艺路线优化决策的问题描述

进行工艺设计，首先要根据工件各特征的加工属性(形状、尺寸、公差和表面粗糙度)确定其加工方法，然后对所有特征的加工方法进行组合排序，这个过程就是工艺路线的优化过程。为了方便工艺路线的描述和遗传操作，将工件特征的某个加工操作定义为加工元，由加工元编号、加工特征、加工方法，以及所使用的机床、刀具、装夹方案组成。将加工元表示为

Op=(ID，Feature，Process，Machine，Tool，Setup)

其中:ID、Feature、Process、Machine、Tool、Setup 分别为加工元编号、加工特征、加工方法、所需的机床、刀具和装夹方案。

设 O={Op1，Op2，…，Opn}为完成工件加工的所有加工元的集合。把工件某一工艺路线表示为

其中:{Opa(1)，Opa(2)，…，Opa(n)}={Op1，Op2，…，Opn}，x为以Opa(1)开始、Opa(n)结束的加工元序列。

工艺路线优化的过程实际上就是根据当前生产环境，生成一个最优化或接近最优化的加工元序列的过程。在生产过程中，常根据实际需要确定目标函数，例如生产成本最低、加工时间最短等，对工艺路线进行评价，那么可以确定目标函数的形式为minF(xi)，其中，F(xi)为xi这一工艺路线的优化评价函数。

在工艺路线的优化决策过程中，还必须满足工艺约束，主要指对优化排序具有重要影响的加工方法之间的优先关系约束。将约束信息用矩阵A［n］［n］表示。

所谓最优工艺路线是指在满足工艺约束的条件前提下，目标函数值最优的工艺路线。其中工艺约束主要是指对工艺路线的优化排序具有重要影响的加工方法之间的优先关系约束。在本文中将工艺约束信息用矩阵 A［n］［n］表示。

基于以上分析，工艺路线优化问题的数学模型可描述为:对于工件的加工元集合 O={Op1，Op2，…，Opn}，寻找一条加工工艺路线 x=＜Opa(1)，Opa(2)，…，Opa(n)＞，使其满足工艺约束 A［n］［n］，且目标函数值最优，即minF(x)。

工艺路线的优化过程实际上就是将约束逐个作用到加工元集合上，使得加工元在一定的排列顺序下，目标函数值最优。

2 工艺约束及其处理方法

2.1 工艺约束的描述

制定合理的工艺路线必须考虑工件加工特征之间和加工方法之间的优先关系约束，主要包括以下几个方面:

(1)先粗后精 对于每个特征，粗加工工序应安排在精加工工序之前进行;对于整个工件，所有的粗加工工序应安排在所有精加工工序之前进行。

(2)先主后次 即先安排工作表面和装配表面的加工，后安排次要表面的加工，而且次要表面安排在最后精加工或光整加工之前。

(3)先基准后其他 作为基准的特征应先加工，然后才加工其他表面。如当两个特征之间存在形位公差时，包含基准的加工特征应当首先加工;加工阶梯轴时，端面特征作为测量基准优先于外圆面加工。

(4)非破坏性约束 保证后面的加工不会破坏在前面加工过程中产生的属性。例如在一个圆柱上加工螺纹和倒角时，倒角应先于螺纹加工。

(5)依赖约束 若某一特征的存在依赖于另一特征，则另一特征先于此特征加工。例如在一个平面上有一个孔特征，那么面特征要先于孔特征加工。

工艺路线必须满足上述约束规则。在约束规则的作用下，加工元之间的优先关系约束表现为执行的先后次序。由于定性的、描述性的约束信息在计算机处理时比较复杂，不便于计算机的底层推理和简化计算，本文通过工艺约束矩阵的方式描述加工元之间的优先关系约束，将定性的优先关系约束信息转化为定量的、数字化的矩阵。

约束矩阵用A［n］［n］来表示，n表示加工元的个数。矩阵中元素aij代表两加工元之间的先后关系，元素值按以下规则进行转换:

2.2 约束矩阵的自动生成

系统根据优先关系约束原则，并结合加工元中的特征信息、加工方法信息、装夹方案等信息，对加工元进行分类，属于不同类别间的加工元具有相应的优先关系，系统按照约束矩阵转换原则将矩阵中相应的元素赋值为1。

以先粗后精原则为例，首先遍历所有加工元，根据各加工元的加工方法，将属于粗加工阶段、半精加工阶段和精加工阶段的加工元划分到其相应集合;由先粗后精原则，有粗加工阶段加工元集合中的元素优先于半精加工阶段加工元集合中的元素，半精加工阶段集合中的元素优先于精加工阶段加工元集合中的元素;最后，根据约束矩阵转换原则将以具有优先关系的两个加工元为下标的元素赋值为1。在处理完由所有原则产生的加工元之间的优先关系后，工艺约束矩阵自动生成。

3 基于遗传算法的工艺路线优化过程

3.1 基因编码

基因编码是应用遗传算法的第一步，常用的二进制编码无法表达工艺路线的排序优化问题。本文采用自然数字链进行基因编码。为便于遗传操作和约束矩阵的生成，将每一个基因对应工件加工元集合中的一个加工元，因此每个基因由6部分组成，分别对应加工元的6个组成部分。在程序中基因用如下的结构体来描述。其中加工元编码与自然数字链一一对应，它是区分加工元的标志，代表加工元进行遗传操作;基因中其他部分代码也都用两位十进制数表示，程序运行过程中需要根据这些代码确定加工元间的优先关系和计算染色体的适应度值。

3.2 初始种群的产生

初始种群是根据工件加工元集合随机生成的一组确定数量的加工元序列。初始种群中可能存在无效的即不满足优先关系的加工元序列，需通过约束矩阵和加工元序列调整算法将它们转化为有效的加工元序列，从而使初始种群中的染色体均符合优先关系约束。

3.3 适应度函数的确定

在工艺设计中，工艺路线一般是通过加工成本最低、加工时间最短等作为评价指标。本文以加工成本最小作为工艺路线的优化目标。加工成本包括机床成本、刀具成本、机床变换成本、刀具变换成本和装夹变换成本。对一个工件的工艺过程来说，在确定各特征的加工方法及其使用的制造资源后，机床成本和刀具成本对每一种加工元序列都是一样的。对不同的加工元序列，加工成本的不同主要体现在机床变换成本、刀具变换成本和装夹变换成本。因此本文以总变换成本最小作为工艺路线的优化目标。总变换成本C、机床变换成本CM、刀具变换成本CT和装夹变换成本CS分别表示如下

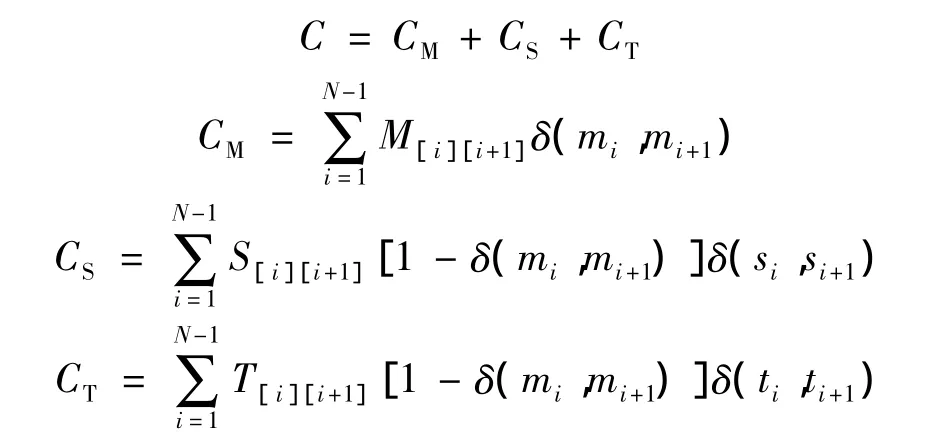
其中，N 表示加工元集合中加工元的个数;M［i］［i+1］、S［i］［i+1］、T［i］［i+1］分别表示某一加工元序列中第 i个加工元与第i+1个加工元的机床变换成本、装夹变换成本和刀具变换成本，在本文中设 M［i］［i+1］、S［i］［i+1］、T［i］［i+1］分别为 20、8、1;mi、si、ti分别表示第 i个加工元中所使用的机床、装夹方案和刀具。对于以上各式有

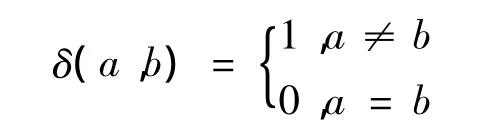
最优的工艺路线是具有最小变换成本的加工元序列，而遗传算法是根据适应度对个体进行评价的，适应度值越大者为较优的个体，因此有必要建立适应度函数与目标函数的映射关系:

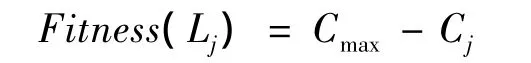
其中:Lj为第j条染色体，Cmax为工艺路线总变换成本的理论最大值，Cj为第j条工艺路线的总变换成本。

3.4 选择

采用排序选择算法和最佳个体保护策略相结合的选择方法。排序选择算子，即对种群中的个体按照适应度值的大小进行排序，然后基于一定的比例，将排在前面具有较高的适应度值的个体复制2份，中间具有稍高适应度值的染色体复制1份，排在最后适应度值较低的个体不复制，所有复制得到的个体构成交配池。排序选择法保证了参与后代的繁衍和进化的是种群中的优良个体［6］。

采用最佳个体保护策略，是为了防止进化过程中最优个体由于参与交叉和变异而被破坏。即每次计算的最优个体除作为交配池的种子之外，还直接作为子代个体。最佳个体保护策略保证了每次计算结果至少不会比上一次差，使进化的方向总是向着最优值的方向逼近。

3.5 交叉

为保证交叉后的染色体有效，采用两点交叉的方式进行交叉运算。具体步骤如下:

(1)首先在交配池中随机选取两个个体作为父代染色体P1、P2，并随机生成两个交叉点，这样父代染色体被分为左半部分、中间部分和右半部分。

(2)将P1的左半部分和右半部分分别复制到子代染色体C1的左右两半部分。

(3)在P2中划掉与P1的左半部分和右半部分完全相同的基因，将P2中剩余的基因按照它们原来的顺序依次复制到C1的中间部分，这样就形成C1。

(4)采用同样方法得到子代染色体C2。图1为交叉过程。

由于父代染色体是有效的染色体，采用两点交叉方法生成的子代染色体也是满足优先约束的，因此不需要调整加工元序列。

3.6 变异

本文采用随机交换染色体中的2个基因代码的位置的变异运算。即在一定的变异率下，选择一部分染色体，在单个染色体内部随机进行2个基因的交换形成新的个体，如图2所示。

表1 基因编码

由于交换2个基因后，可能会出现无效的即违反优先关系约束的染色体，因此，变异运算完成后，要判断新生成的个体是否有效。如果无效，则需通过调整算法将其转化为有效的染色体。在这里，只需调整两个交换点之间的基因序列，因为交换位置以外的基因序列本身就满足优先关系约束，只要保证交换点之间序列的有效性，就能保证整条染色体的有效性。

3.7 加工元序列有效性检验与调整算法

在初始种群生成和遗传操作过程中，生成的加工元序列可能会不满足优先关系约束。为了在遗传算法运行过程中保证个体的有效性，须根据工艺约束规则确定的加工元优先关系约束矩阵对个体进行有效性检验和调整。

设某一个体表示的加工元序列为

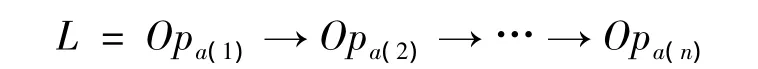
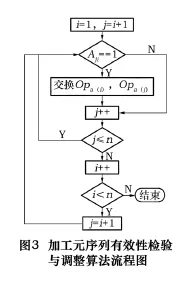
图3为算法流程图。

步骤1:遍历加工元序列L，从Opa(1)到Opa(n)，设i=1，j=i+1;

步骤2:搜索约束矩阵，如果Aji=1，说明加工元Opa(j)优先于加工元Opa(i)，应互换Opa(i)和Opa(j)，并使j++。否则，直接使j++。

步骤3 判断是否j≤n，如果真，则转到步骤2;否则令i++，并转到步骤4。

步骤4 如果 i＜n，令j=i+1，转到步骤2，否则结束。

3.8 终止条件

为保证遗传算法在保证具有较优解的基础上正确退出，以连续迭代 1 000次，或最优个体的适应度值连续迭代200次保持不变为终止条件。

计算终止后，输出适应度值最大个体对应的加工元序列，作为工件的工艺路线。

4 应用实例

以图4所示的花键套工件为例来说明该算法的实现过程。

首先在明确各特征及其加工方法、定位基准和制造资源之后，进行基因编码，如表1所示。

然后根据特征、加工方法、装夹方案等信息和优先关系约束原则，确定加工元之间的优先关系，并建立描述优先关系的工艺约束矩阵。

设种群规模为80，交叉率为0.8，变异率取0.2，迭代次数达到1 000或最高染色体的适应度值经过200次迭代仍保持不变为终止条件。经过1 000次迭代，程序运行停止，得到适应度值最高的染色体的适应度值为393，其对应的工艺路线如表2所示。其中更换机床的次数为3次，更换夹具的次数为4次，更换刀具的次数为16次。该优化结果表明基于遗传算法和约束矩阵的工艺路线优化算法是可行有效的。

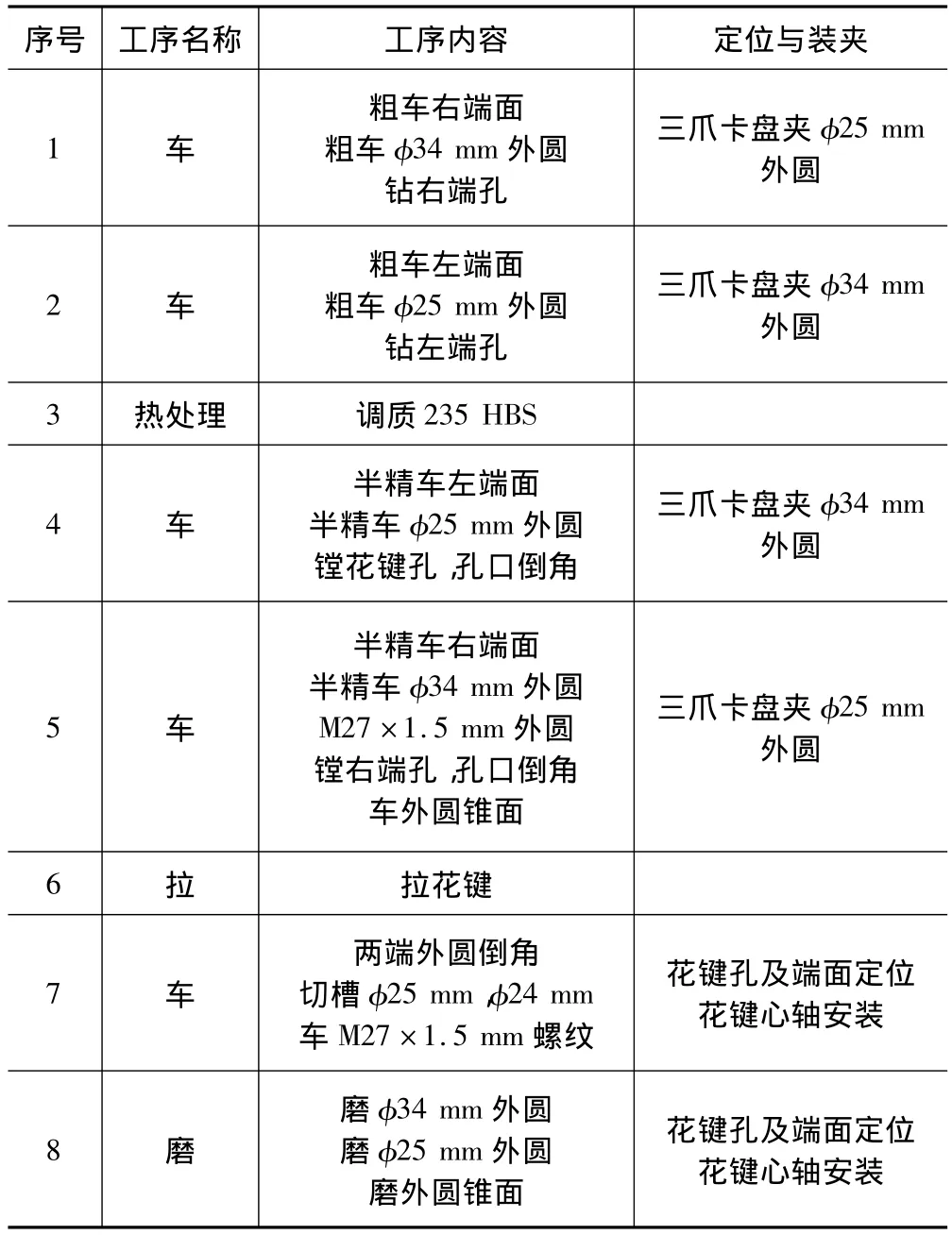
表2 最大适应度值染色体对应的工艺路线

5 结语

本文提出的基于遗传算法和约束矩阵的工艺路线排序优化方法，是CAPP中解决工艺路线优化问题的有效实用方法。利用约束矩阵来描述加工元之间的优先关系，并由系统自动生成约束矩阵，开发了不依赖于特定规则的加工元序列有效性检验与调整算法，以总变换成本最小为优化目标，利用改进的遗传算法对工艺路线排序进行启发式全局寻优，实例验证了该算法的可行性和有效性。

［1］邵新宇，蔡力钢.现代CAPP技术与应用［M］.北京:机械工业出版社，2004.

［2］朱海平，肖诗旺，黄刚.基于遗传算法的工艺过程排序研究［J］.华中科技大学学报:自然科学版，2006，34(3):50－53.

［3］刘连发，张振明，田锡天，等.基于遗传算法的工艺路线优化决策方法研究［J］.机械制造，2008，46(526):59－62.

［4］王忠宾，王宁生，陈禹六.基于遗传算法的工艺路线优化决策［J］.清华大学学报:自然科学版，2004，44(7):988－992.

［5］张国辉，蔡力钢，高亮，等.基于改进遗传算法的工艺路线优化［J］.机械设计与制造，2006(8):14－16.

［6］任庆生，叶中行，曾进，等.对常用选择算子的分析［J］.上海交通大学学报，2004，34(4):564 －566.