水利工程曲底明槽水面线计算分析

宁 燕

(陕西省水利电力勘测设计研究院，陕西 西安710001)

在用经典方法计算水面线时，已有研究最多的便是棱柱体明槽水面线计算，且多是固定坡度求解，但目前在一些大型工程中，曲面底坡渠槽也大量采用，如溢流堰曲线段，龙抬头曲线段，泄水槽的欧奇段，因为曲线底坡明槽可以很平缓实现底坡的过渡，使水流流态平稳.这些曲底明槽为非棱柱体明槽，目前在经典水力计算中介绍不全面，鉴于此，本文对曲其水面线计算公式进行了推导，得出了一套较完整的经典明槽水面线计算方法.供设计参考。

1 计算公式的导出

明渠恒定非均匀流的基本微分方程为:

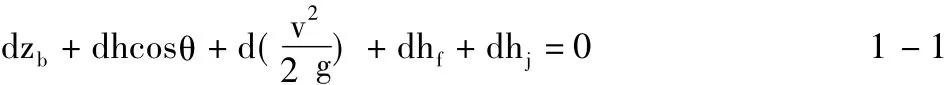
式中:dzb为位置水头微分，h为垂直槽底水深，v为水流流速，dhf为沿程水头损失，dhj为局部水头损失，局部水头损失在计算渐变流水面线过程中可忽略不计。

且，dzb= －sinθds;d (θ为该处切线与水平面夹角，dhf可近似用均匀流计算公式确定，则为摩阻坡度.对于曲底明槽，基本方程可写为:

将摩阻坡度的表达式代入，且谢才系数用曼宁公式表示后有:

由于坡度i为变量，这里将i表示为底坡变化的斜率fˋ(x)，则cosθ可表示为，sinθ 可表示为则曲底明槽的水面线基本方程可写成:

2 曲底明槽水面线求解

在计算中，由于曲线长度s在计算中较为不便，这里将其化为x的函数，则有:

若过流断面为矩形，则上式可简化为:

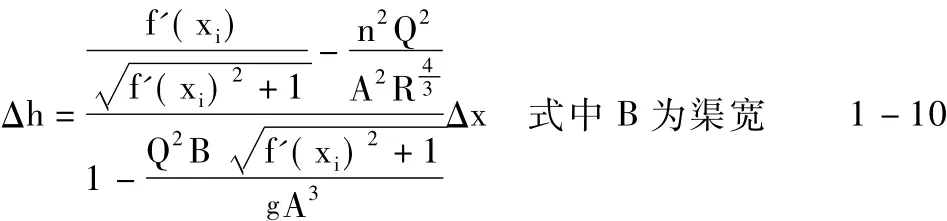
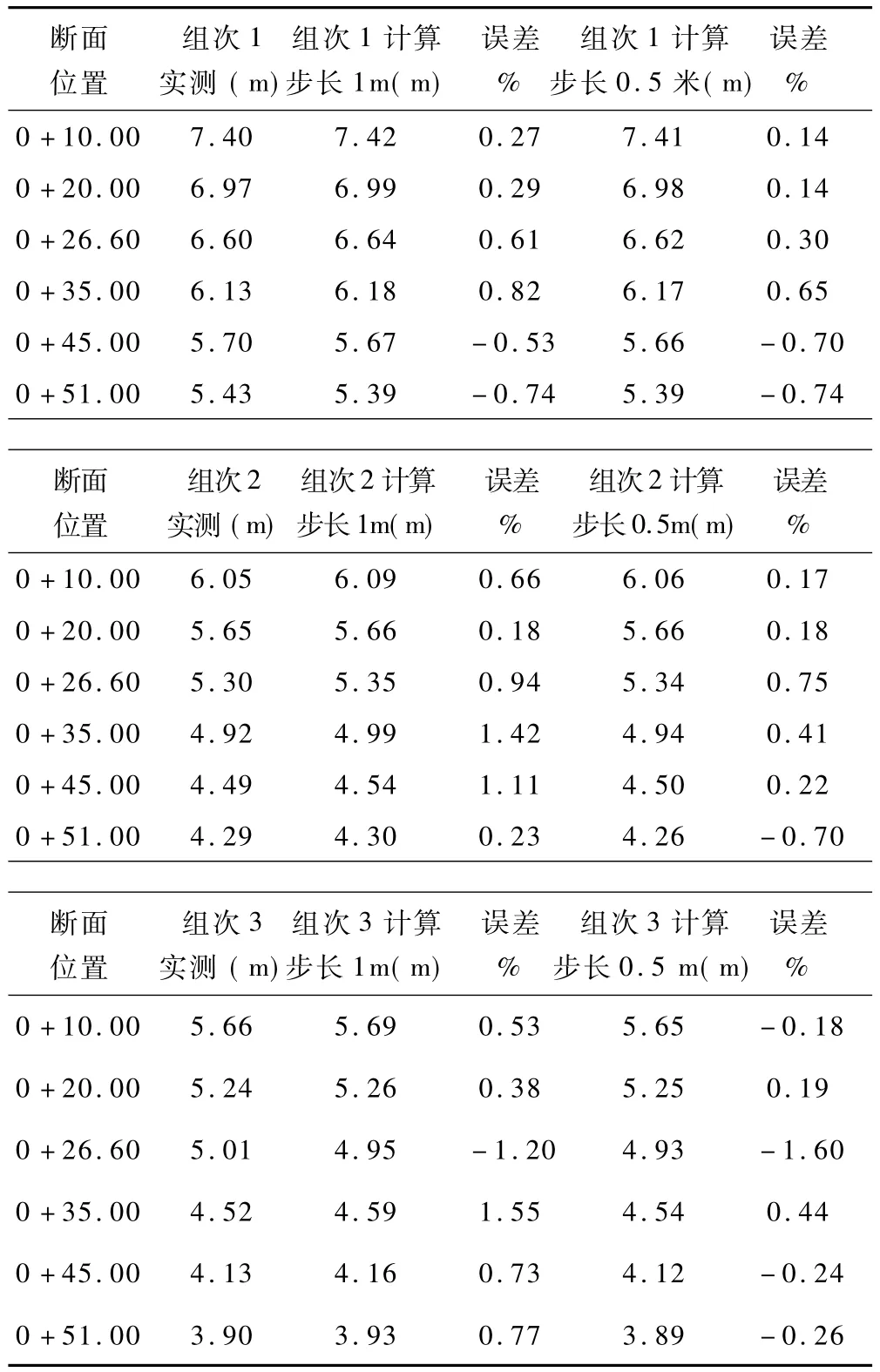
表1 不同步长计算值与实测资料对照表

3 计算实例及试验验证

本文所取算例为一抛物线槽底，其渥奇曲线方程y=0.02x+0.00666x2，渥奇段下接坡度 i=0.667 的 斜坡段，用式1—10计算可得如下结果.并与实测资料进行了对比。

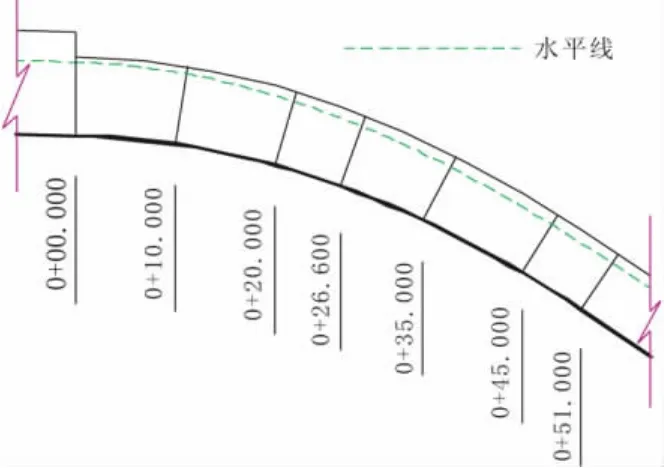
图1 试验明槽纵剖面图

4 结论

计算结果与实测资料对比发现计算最大误差不超过1%，并且随着步长的减小而精度增加。因为步厂越小，计算沿程水损时越接近均匀流假设.说明用该公式可以很精确的进行曲底明槽水面线计算，还可模拟任意棱柱体陡坡缓坡的水面线，只需将斜率定为常数即可.

从误差数据可看出随着计算向下游进行，误差有增大的趋势，其原因有两个，一个就是局部水头忽略的影响，因为曲底明槽与棱柱体明槽相比较而言，曲底明槽几何特性变化较大，其局部水头损失影响较棱柱体明槽严重。另一个就是沿程水头损失的影响，及糙率影响，实验中糙率的微小误差，均可影响计算结果，若误差累计，则会出现误差随计算进行有增大的趋势。

［1］清华大学水力学教研组.水力学(1980年修订版)高等教育出版社1980

［2］高学平.陡槽水面线的计算［J］.水力发电学报 1995年第4期，总51期

［3］孙道宗.非棱柱体明渠非均匀渐变流水面线定性分析与计算［J］.江西水利科技 ，1996，22(4):

［4］郑小玉，杨永全.明渠水流模型试验中糙率不相似问题研究［J］.四川大学学报(工程科学版)，2003，35(4):

［5］黄佑生 顾令宇.一种新的水面线计算方法［J］.水利水电科技进展 ，2003，23(3):