海冰重叠动力条件分析

李春花,孙鹤泉

(1.国家海洋环境预报中心国家海洋局海洋灾害预报技术研究重点实验室,北京 100081;2.大连舰艇学院,辽宁 大连 116018)

海冰重叠动力条件分析

李春花1,孙鹤泉2

(1.国家海洋环境预报中心国家海洋局海洋灾害预报技术研究重点实验室,北京 100081;2.大连舰艇学院,辽宁 大连 116018)

由于重叠冰厚度较大,给冰区海洋运输以及海洋生产作业等带来较大影响,为了得到科学客观的重叠冰厚度,需要对重叠冰的形成条件进行深入研究。利用理论分析和数值模拟方法,分析了波浪、风和流对渤海海冰重叠的影响。通过理论计算分析发现,波浪是导致海冰断裂的主要因素;采用离散元方法对海冰重叠过程进行了数值模拟,模拟结果表明海冰在外界动力作用下,海冰初始发生屈曲变形断裂,随后产生重叠。综合分析表明,海冰在同时具备波浪的垂向波动作用以及风或流水平作用力下,冰层比较容易发生重叠,波浪对海冰重叠的作用不可忽略,海冰的重叠长度取决于风和流作用的大小,其作用力越大,重叠长度越大。

海冰;重叠冰;渤海;动力条件

Abstract:The rafted ice can prominently affect navigation and platform production for its rather great thickness.Studying its forming condition is important in analyzing the reliability of ice design parametersof offshore structure.Theoretical analysis and numerical simulation have been applied to discuss the effectofwave,current and wind on the ice rafting.The Theoretical analysis results show thatwave is the key factor for ice fracture.The processof ice rafting is simulated by using the discrete elementmethod,and the simulated results show that the distortion and flexure breakage are happened initially and rafting followed then.The synthesisanalysis results show that the ice iseasily rafted under the joint action ofwave,current and wind,and the actionofwave can′t be ignored.Moreover,the rafted ice length increaseswith the increasing force of ocean current and wind.

Key words:sea ice;rafted ice;Bohai Sea;dynamic condition

在渤海,海冰的重叠现象随处可见,重叠冰是该海域的主要海冰类型之一。由于重叠冰存在的普遍性及其厚度较一般单层冰厚度偏大,因此给冰区海洋运输以及海洋工程施工、生产作业等带来较大的影响。我国关于重叠冰的观测资料较少,对渤海重叠冰问题的研究也不多,为了获得重叠冰的特征参数,需要对重叠冰的形成条件和特点进行深入的研究。

国际上对重叠冰的研究源于北极海冰,北极海冰的重叠现象也比较常见,尤其在结冰初期或季节性结冰区,人们通过大量的现场调查、理论分析、数值模拟以及物理模型试验等方法对重叠冰问题进行了研究和探讨。通过对北极海盆重叠冰的研究结果发现,海冰从发生重叠到形成冰脊的冰厚过渡范围为0.15～0.3m[1];Parmerter通过模型计算获得不破碎冰层的最大重叠厚度为0.17 m,但同时他指出,由于海冰的温度、盐度影响其强度,在有些海域也可能出现更厚的冰层产生重叠的现象[2];有学者曾在波弗特海中央观察到3.3 m厚的冰层发生重叠[3];近些年人们对海冰的重叠问题进行了更为深入的研究,Hopkins等通过数值模拟和室内实验对冰层发生重叠的临界条件进行了分析和实验验证,着重研究了冰厚以及冰厚不均一性对海冰重叠的影响[4-5];Babko分析了海冰重叠在北极海冰冰厚分布中的作用,并指出海冰重叠是影响冰厚分布的重要因素之一[6]。通过调查研究表明,不同海域海冰的重叠特点各不相同。

我国学者对渤海海冰的重叠问题进行了部分调查研究工作[7-8]。渤海重叠冰主要包括两种类型,一种是指状重叠冰,它主要发生在海面刚冻结形成的冰皮当中,此时海冰厚度较薄,强度较小,在外界驱动力下,冰皮以剪切方式破坏并发生重叠,从而形成指状重叠冰[7];另一种是层状重叠冰,随着海冰厚度增长,强度增大,海冰很难发生剪切破坏,此时海冰主要发生弯曲或屈曲破坏,弯曲破坏主要发生在垂向荷载作用下,如波浪作用,而屈曲破坏则主要发生在水平荷载作用下,如风和流作用,断裂的冰层在环境驱动力下可以爬到另一块冰层上,这就形成了层状重叠冰。

基于当前的研究现状,利用理论分析和数值模拟方法探讨了波浪、风和流对渤海海冰重叠的作用。结合波浪理论、力学平衡原理和弹性薄板理论,计算分析了海冰在波浪、风和流等不同驱动力作用下的断裂长度和重叠长度;假定海冰为粘弹性体,采用离散元方法对不同条件下海冰重叠过程进行了数值模拟。结果分析表明,波浪对海冰重叠的作用不可忽略,海冰重叠长度与风和流的作用密切相关。

1 波浪、风和流对海冰重叠作用的理论分析

由于重叠冰的形成与当地的水文气象条件密切相关,不同海区重叠冰有其各自的特点,重叠方式也不尽相同。在渤海波浪、风和流等外界驱动力是影响海冰是否发生重叠的重要动力因子。

海冰必须断裂后才能发生重叠,因此我们首先分析海冰的断裂条件。假定海冰为半无限长弹性梁,其非重叠一端由于是无限长,因此不考虑其转角与纵向位移,在冰排重叠过程中始终视为固支约束,即限制冰排沿垂直方向的平动,但允许冰排绕支座转动,重叠端视为自由端[8]。波浪对海冰主要是垂向作用力,风和流对海冰产生的则是水平作用,图1是冰排在波浪作用下产生弯曲断裂的示意图,即A截面弯曲应力达到其极限应力时海冰发生断裂;图2描述的是冰排在风或流作用下产生屈曲断裂,即当B截面处挤压应力达到屈曲破坏条件时海冰发生断裂,具体分析如下。

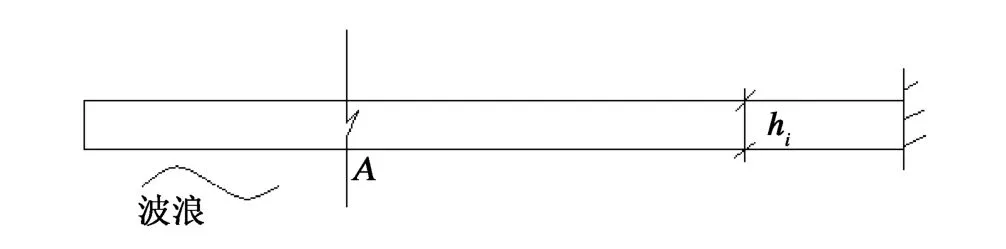
图1 冰排在波浪下断裂Fig.1 Ice fracture underwaves

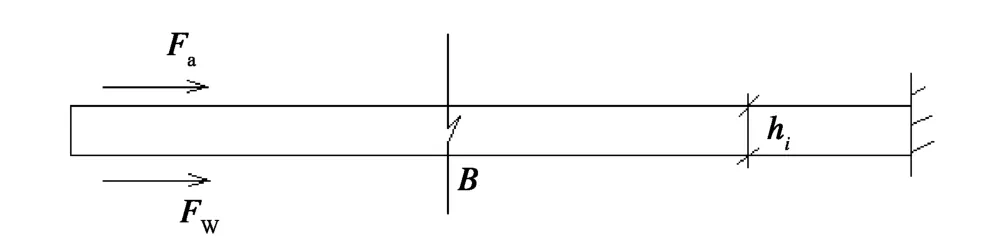
图2 冰排在风、流作用下断裂Fig.2 Ice fracture under current and wind

1.1 波浪作用下的海冰断裂

波浪作用下的海冰断裂[9],对应冰层变形的弯曲应力可以应用弹性薄板弯曲理论来计算

式中:ki为冰盖下波浪的波数;Hi为冰盖下的波高;冰层覆盖下的波高与开阔水的波高之比为

式中:k为开阔水波浪的波数;H为开阔水的波高;d为水深;ρw为海水密度;c和ci分别为开阔水和冰盖下的波速。

在波峰x-cit=0处的弯曲应力σhi/2最大为

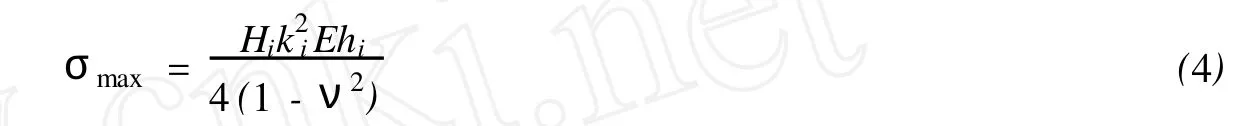
当σmax达到冰的弯曲强度σf,海冰即发生断裂。对于相同厚度的冰层,海冰弹性模量越大,冰层越容易断裂;相同的冰层,波周期越小,冰层越容易断裂[10];冰层的断裂长度与波长有关,因此在波浪作用下冰层典型断裂长度为几十到几百米的尺度。在渤海,由于海冰厚度较小,通常0.2～0.5 m的波高就能使冰层断裂。渤海的年均波高为0.5～1.0m,而年中波高以冬季最大,波高2m以上的频率在20%以上,由此分析,渤海海冰在波浪作用下非常容易断裂。

1.2 风和流作用下的海冰断裂

在风和流作用下,海冰发生屈曲破坏的条件是,冰排某段面处内力达到冰排屈曲破坏力[8],即

且P不大于极限抗压力Pc=hiσc,σc为海冰极限抗压应力。式(5)中,C为边界条件修正系数,取值为2,E为海冰弹性模量,υ为泊松比,hi为海冰的厚度,ρw为海水密度,取值为1 025 kg/m3。根据P≤Pc,可以得到冰排发生屈曲破坏的极限冰厚条件为

当极限抗压应力σc越大,对应的极限断裂冰厚值越大,即海冰越不容易断裂;当海冰弹性模量E越大,对应的极限断裂冰厚值越小,即海冰越容易断裂;取渤海海冰力学参数典型值E=3 GPa,υ=0.3,σc=2 MPa,可得海冰发生屈曲断裂的极限冰厚为0.36 m左右。

根据力的平衡关系,此时满足

式中:Fa和Fw分别为风和流对海冰的拖曳力,Fa=CaρaV2aL,Fw=Cwρw|Vw-Vi|(Vw-Vi)L。其中,ρa为空气的密度,取值为1.029 kg/m3,Ca和Cw分别为空气和水的阻尼系数,它们分别依赖于大气边界层和冰下海洋边界层的物理特性以及冰面和冰底的形状和粗糙度[11],该系数对拖曳力的计算结果有较大影响,取较大值1.64×10-3和0.01,以保守计算。Va、Vw和Vi分别为风速、流速和海冰速度,L为海冰断裂长度,即自由端到断裂处的长度。

假定没有风,仅在流的作用下,海冰断裂条件为P=Fw,由此可得到海冰断裂长度与水流速度关系:

图3为海冰断裂长度与流速、冰厚的关系曲线,由图可见,对于相同冰厚,流速越大对应的海冰断裂长度越小;相同流速条件下,冰厚越大,对应海冰断裂长度越大;取弹性模量和冰厚较小值,即E=1 GPa,hi=0.05 m,流速较大值Vw=1.0 m/s,冰速Vi=0,以分析极限情况,得到冰排断裂长度为10.44 km,海流速度越小,冰厚越大,海冰弹性模量越大,相应的冰排断裂长度越长。

同理,假定没有海流作用,仅在风的作用下,海冰断裂的条件为P=Fa,由此可得到海冰断裂长度与风速的关系:

图4为海冰断裂长度与风速、冰厚的关系曲线,相同冰厚,风速越大对应的海冰断裂长度越小;相同风速条件下,冰厚越大,对应海冰断裂长度越大;取弹性模量和冰厚较小值,即E=1 GPa,hi=0.05m,风速取较大值Va=20m/s,得到冰排断裂长度为31.77 km,而渤海平均风速一般为6～7 m/s,可见,只在风的作用下,海冰的断裂尺度基本在几十公里以上。

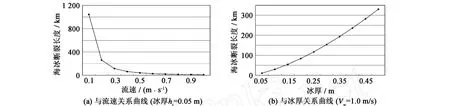
图3 海冰断裂长度与流速、冰厚的关系(E=1 GPa)Fig.3 Ice fracture length versus current velocity and ice thickness

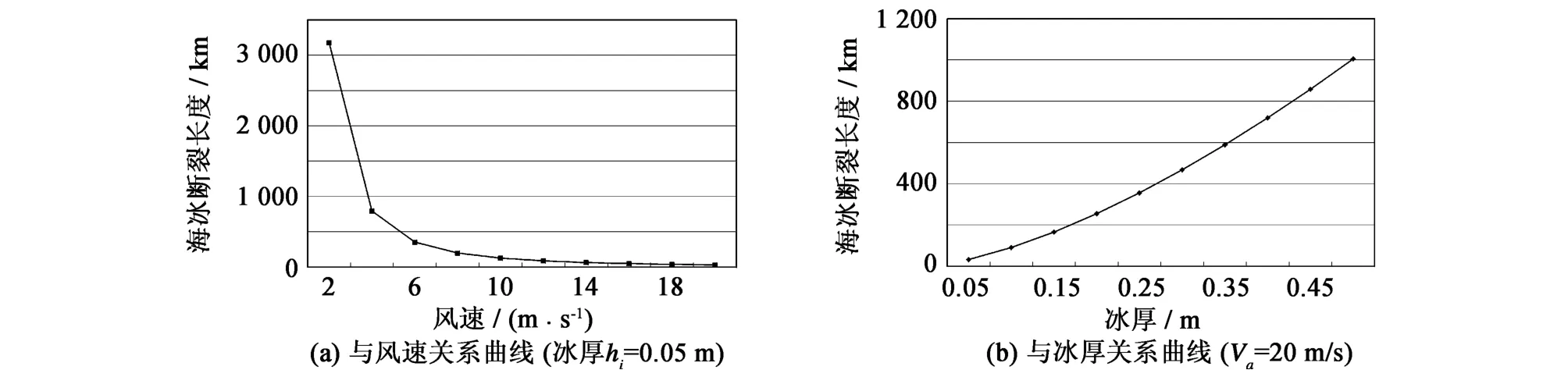
图4 海冰断裂长度与风速、冰厚的关系(E=1 GPa)Fig.4 Ice fracture length versuswind velocity and ice thickness

由以上计算数据分析,仅在风或流作用下,海冰断裂的尺度都比较大,该模型适合于分析尺度较大的冰原断裂情况。对于10 km以下尺度的海冰,主要是波浪的作用使其断裂。

1.3 风和流作用下的海冰重叠

断裂后的冰排视为自由漂浮冰排,长度为L,在风作用力Fa和流作用力Fw的联合作用力驱动下,与前端半无限漂浮冰排产生重叠,见图5,重叠长度为Lc,在重叠处产生摩擦力Fr,随着重叠长度的增加,摩擦力增大,当其增大到足以抵抗风和流对冰排产生的外界驱动力时,此次重叠过程结束。即为

式中:Fr=μρighiLc;μ为海冰摩擦系数,对于渤海海冰其值取为0.4;ρi为海冰的密度,取值为880 kg/m3。

整理式(10),可以得到

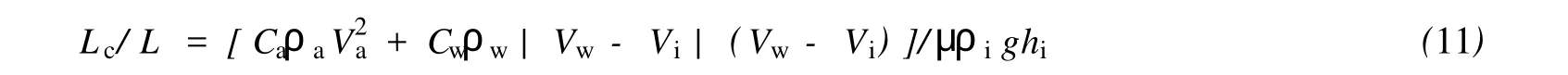
由式(11)分析,如果在相同的外界驱动力下,冰排厚度越薄,重叠的海冰长度越长,反之,海冰厚度越大,重叠长度越短。而对于相同厚度的冰排,如果风速和流速越大,则发生重叠的长度越长。图6是海冰重叠长度与冰厚的关系曲线,风速取较大值Va=20 m/s,流速也取较大值Vw=1.0 m/s,海冰重叠长度与原始海冰长度的比值是随冰厚增加而减小的。对于尺度为1 000m,厚为20 cm的冰层,其重叠长度约为16m,如果冰厚为10 cm,重叠长度则为31 m左右,可见冰厚对海冰重叠长度的影响很大。在通常的风速和流速作用下,海冰的重叠长度会更小,尺度在1～15m。

图5 冰排在风、流作用下产生重叠Fig.5 Ice rafting under current and wind

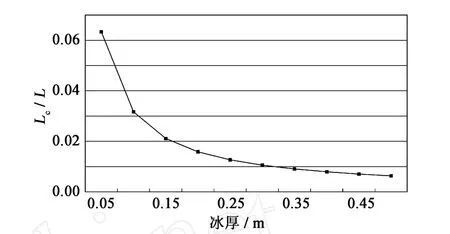
图6 海冰重叠长度与冰厚的关系(Va=20m/s,Vw=1.0m/s)Fig.6 Ice rafting length versus ice thickness

2 海冰重叠数值模拟

利用离散元方法对冰层的断裂重叠过程进行数值模拟。首先离散冰排,设定边界,图7为海冰重叠数值模拟初始状态图,1～N为离散的冰块单元数,假定在冰排中部即N/2单元块处存在初始断裂,赋予2～N/2单元块体初始垂向速度v0,1单元块体保持静止,模拟该端为固定端,赋予N/2+1～N单元块体固定的水平速度u0及初始垂向速度v0,并让N块体始终保持u0的水平速度,以此简化模拟海冰的初始状态和风、流、波浪对海冰的作用。

图7 海冰初始状态Fig.7 First state of ice sheet

2.1 海冰基本方程

冰层满足牛顿定律的动力学方程[12]:

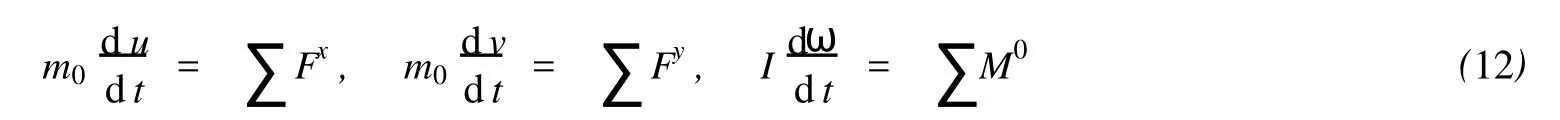
式中:m0为冰层质量;I为冰层对质心的惯性矩;u,v,ω分别对应于冰层质心的水平速度、垂向速度和角速度;Fx,Fy,M0分别为冰层受到的水平力、垂向力及各力对质心的力矩。

断裂后的冰块依然满足牛顿定律,第i个冰块在运动及块体间相互作用时,满足以下方程:

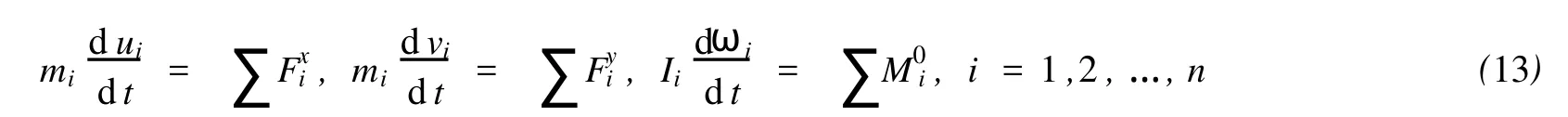
式中:mi为i冰块质量;Ii为i冰块对质心的惯性矩;ui,vi,ωi分别对应于i冰块质心的水平速度、垂向速度和角速度;Fxi,Fyi,Moi分别为i块体受到的水平力、垂向力及各力对质心的力矩。

在本模型中假定海冰为粘弹性体,材料的线粘弹性性质,可以用模型来表示和描述。最简单的粘弹性模型由一个弹簧和一个阻尼器串联或并联而成,即Maxwell模型和 Kelvin模型。本数值模型中对海冰采用Kelvin粘弹性模型,Kelvin模型由弹簧和阻尼器并联而成,两个元件的应变都等于模型的总应变ε,而模型的总应力为两元件应力之和[12],即海冰内部应力满足

式中:σ、ε分别为正应力和正应变,E为材料拉压弹性模量,η为粘性系数,dε/dt为应变率。

由于假定冰层为粘弹性体,当冰层与冰层相互作用时,冰层产生变形,冰层内部作用力包括弹性力和粘性力,弹性力的大小与冰层弹性模量E以及冰层变形有关,粘性力与冰层粘性系数以及冰层变形率有关,当冰层内部最大挤压应力或拉伸应力超过其极限抗压或抗拉强度时,冰层即发生断裂。

冰层断裂后形成一些离散块体,假定离散块体间碰撞为粘弹性作用,kne,kte,knv分别为块体间法向弹性刚度、切向弹性刚度及法向粘度,μ为块体间的摩擦系数。i块体与j块体发生碰撞作用时的法向作用力Fni,j及切向力Fti,j与以上各参数有关,法向作用力的计算类似于粘弹性本构关系中Kelvin模型中的应力计算,块体间的切向力最大不超过块体间的摩擦力,即满足摩尔-库仑定律,具体计算式:

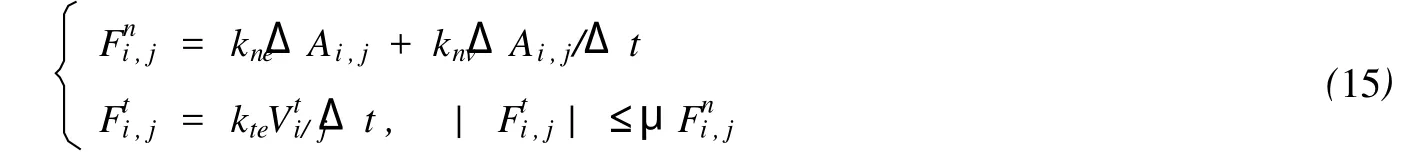
式中:ΔAi,j为块体变形面积;Δt为计算时间步长;Vti/j为i块体相对j块体的切向速度。将Fin,j,Fti,j转换为整体坐标系x-y上的分力Fxi,j,Fy

式中:nx,ny为i块体与j块体相互作用时i块体的作用面法线向量沿x,y轴方向的分量;Moi,j为j块体对i块体质心的作用力矩;rxi,j,ryi,j分别为力作用点到i块体质心距离的x分量和y分量。计算得到各块体之间的作用力,利用式(13)即可获得各块体运动参量,实现海冰重叠过程模拟。

2.2 数值模拟结果

图8和9是通过数值模拟得到冰厚分别为5 cm和25 cm的海冰重叠过程图。图中(a)-(f)选取的是海冰重叠过程中的典型位置状态,主要计算参数见表1。由图中可以很直观的看到,在外界动力作用下,海冰初始发生屈曲变形,随后在断裂处分离,产生重叠;在同一时间间隔,相同动力作用下,冰厚较薄的冰排,其重叠长度较长,而较厚的冰块,其重叠长度则较短。

通过数值模拟试验还发现,如果冰厚越薄,海冰越容易发生重叠;如果v0=0,即对海冰的外驱动力不存在垂向作用时,海冰很难产生重叠;冰下海水的波动导致海冰垂向波动越大,海冰越容易重叠。

表1 数值模拟参数Tab.1 Input parameters for ice rafting simulations

图8 数值模拟海冰重叠过程(hi=5 cm)Fig.8 Ice rafting processwith ice thicknesshi=5 cm

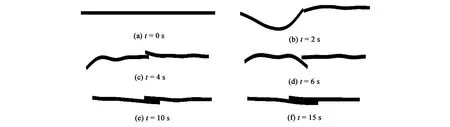
图9 数值模拟海冰重叠过程(hi=25 cm)Fig.9 Ice rafting processwith ice thicknesshi=25 cm

3 结 语

根据理论计算和数值模拟结果分析发现,波浪、风和流是导致渤海海冰断裂重叠的主要动力因子。具体结论:

1)在渤海,通常0.2～0.5m的波高就能使冰层断裂,对于10 km以下尺度的海冰,波浪是导致海冰断裂的主要因素。

2)海冰的厚度和水平动力决定海冰重叠长度,风和流水平作用力越大,冰厚越小,海冰的重叠长度越长,在渤海通常的风速6～7m/s和流速0.5～0.6m/s作用下,海冰的重叠长度一般在1～15m的尺度。

3)海冰在同时具备波浪的垂向波动作用以及风或流水平作用力下,冰层比较容易发生重叠。以往的研究多考虑风和流对海冰重叠的作用,而较少考虑波浪的贡献,本研究发现波浪对海冰重叠的作用不可忽略。

在历次的现场调查中都发现,在冰水交界处,海冰发生重叠的现象比较多,其原因主要是该处同时具备风、流以及波浪的条件,并且冰水交界处的海冰厚度一般较薄,因此较容易产生重叠现象,理论分析结果与此现象相符。

除了波浪、风和流等动力因子,影响海冰重叠的因素还很多,通过简化处理,获得的只是理想化的初步分析结果,渤海重叠冰问题还有待进一步深入地调查和研究。

[1] WeeksW F,Kovacs A.On pressure ridges[R].Cold Reg Res.and Eng.Lab.,HANOVER,N H,1970:IR505.

[2] Parmerter R R.A mechanicalmodel of rafting[J],AIDJEX Bull,1974(23):97-115.

[3] Kovacs A,Mellor M.Sea icemorphology and ice as a geologic agent in the southern Beaufort Sea[C]∥The Coast and Shelf of the Beaufort Sea,Proceedingsof the Arctic Institute of North America Symposium on Beaufort Sea Coast and Shelf Research.1974:113-161.

[4] HopkinsM A,Tuhkuri J,Leosu M.Rafting and ridging of thin ice sheets[J].Journal of Geophysical Research,1999,104(C6):13605-13613.

[5] HopkinsM A,Frankenstein S,Thorndike A S.Formation of an aggregate scale in Arctic sea ice[J].Journalof Geophysical Research,2004,109(C01032):1-10.

[6] Babko O,Rothrock D A,Maykut GA.Role of rafting in themechanical redistribution of sea ice thickness[J].Journal of Geophysical Research,2002,107(C8):2701-2714.

[7] 李志军,丁德文,隋吉学,等.辽东湾多层重叠冰单层厚度的理论分析[J].海洋环境科学,1997,16(4):21-25.

[8] 季顺迎,岳前进,聂建新.渤海海冰的重叠长度分析[J].中国海洋平台,2001,16(5-6):12-16.

[9] 李春花,王永学,邱大洪.波浪传入冰层覆盖水域后的变形[J].中国海洋平台,1999,14(2):10-14.

[10] Wang Y X,Li CH,Li GW,etal.Experimental investigation on breakup of ice floeonwaves[J].China Ocean Engineering,2000,14(4):511-516.

[11] 吴辉碇,白 珊,张占海.海冰动力学过程的数值模拟[J].海洋学报,1998,20(2):1-13.

[12] 李春花,王永学,李志军,等.半圆型防波堤前海冰堆积模拟[J].海洋学报,2006,28(4):172-177.

Analysison dynamic conditionsof ice rafting

LIChun-hua1,SUN He-quan2
(1.Key Lab of Research on Marine Hazards Forecasting,National Marine Environmental Forecasting Center,Beijing 100081,China;2.Dalian Naval Academy,Dalian 116018,China)

P731.15

A

1005-9865(2011)01-0068-07

2010-06-23

国家自然科学基金资助项目(40506009);国家科技支撑计划课题资助项目(2006BAC03B01);海洋公益性行业科研专项资助项目(200805009)

李春花(1973-),女,广东梅县人,研究员,主要从事海冰预报与研究。E-mail:lch@nmefc.gov.cn